Where will a seesaw balance?

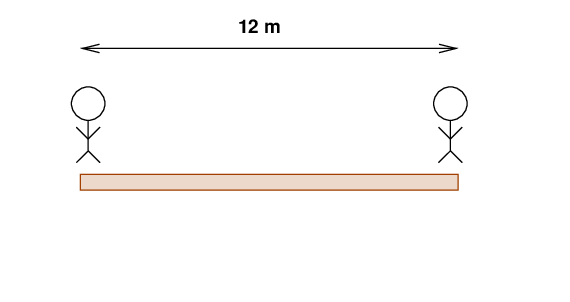
Billy and Alice are playing in the park. They find a big seesaw, with a plank 12 m long (which, amazingly, has zero mass). Each child stands at one end of the plank.



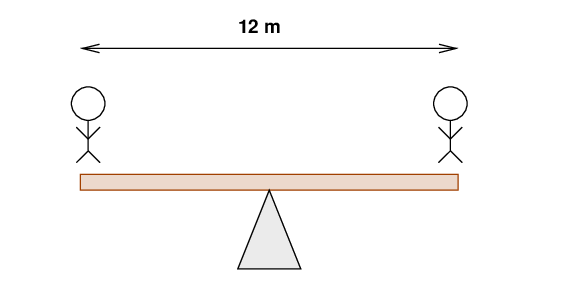
  Q:  Where must the plank be supported in order for the
             device to be perfectly balanced?

The fulcrum must be directly beneath the MIDDLE of the plank, 6 meters from each end. The answer is obvious by symmetry -- one doesn't need any math to see it.

But what if things are a bit different? Suppose that Alice's twin sister Anne joins her at the right-hand end of the plank?



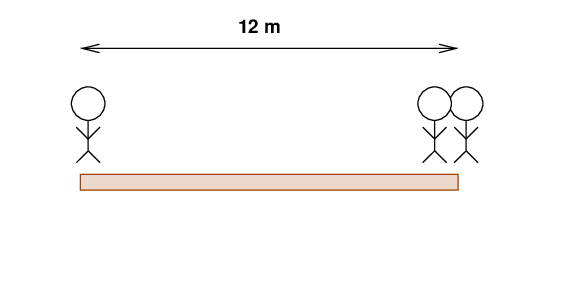
  Q:  Where must the plank be supported in order for the
             device to be perfectly balanced?

Putting the fulcrum under the middle of the plank won't work this time, because there will be more mass on the right-hand side. In order to make the plank balance properly, we need to move the fulcrum closer to the twins. In fact, since there are TWO children on the right and just one on the left, we need to move the fulcrum so that the left-hand section is TWO times longer than the right-hand section.

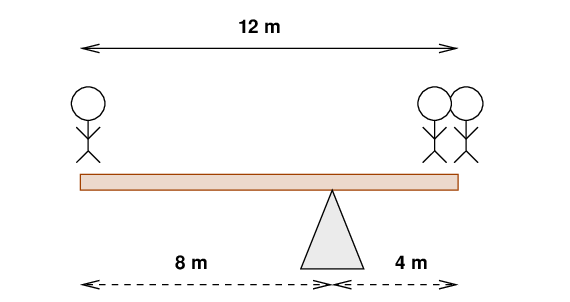
In order to find the balance point, or center of mass, of a system, we need to account for a combination of



      (amount of mass)  *  (distance from balance point)