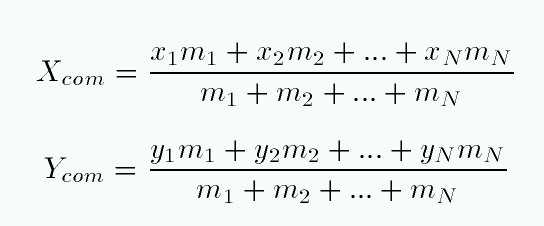
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Given several compact objects of known mass and position, you can find the center of mass of the group in the following way:
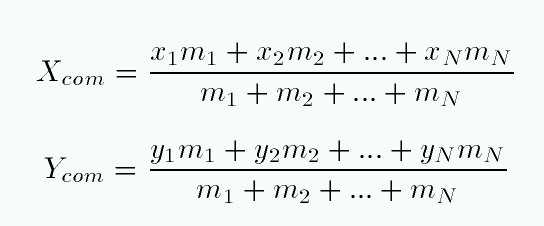
or, in a more compact notation,
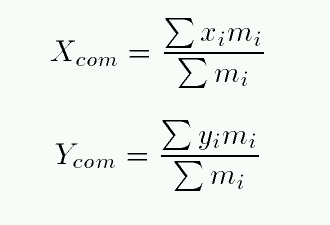
This method will work well as long as the size of each object is much smaller than the distance between the objects.
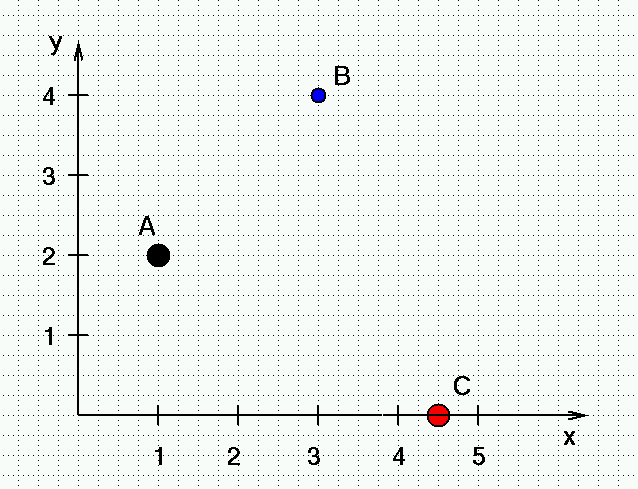
Example: given the 3 small objects in the picture below, with masses A = 5.0 kg, B = 2.0 kg, C = 4.0 kg, what is the location of their center of mass?
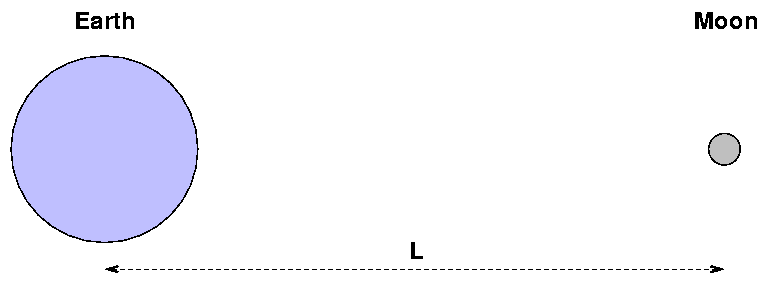
The Earth, mE = 5.98 x 1024 kg, sits on the origin, at position x = 0. The Moon, mm = 7.35 x 1022 kg, is on average at L = 3.84 x 108 m. Where is the center of mass of the Earth/Moon system? Is it inside or outside the Earth?
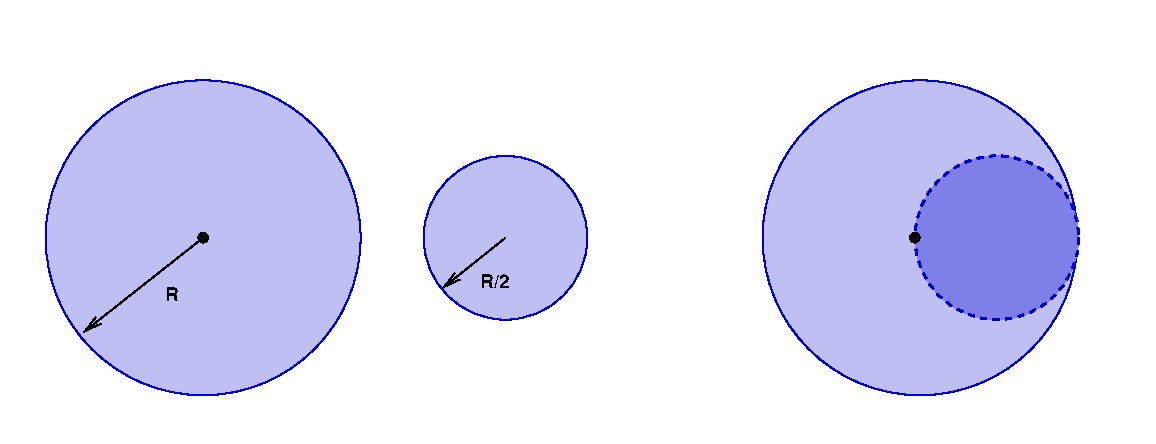
Joe cuts two circles out of a large slab of sheet metal, which has surface mass density σ kg per square meter. The big circle has radius R, while the small circle has radius R/2.
Joe places the small circle on top of the big one, as shown at right in the diagram above.
Joe makes a circle of radius R out of sheet metal. He then cuts out a smaller circle of half the radius, R/2, so that it just touches the edge of the big circle.
Where is the center of mass of the remaining metal?
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.