Analyzing the ballistic pendulum

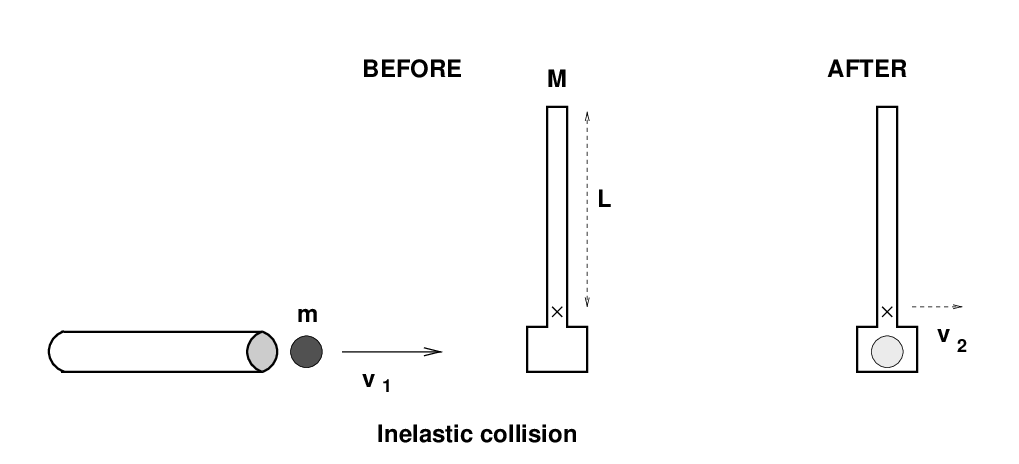
The basic idea is to fire a projectile of mass m at some unknown speed v₁ so that it is caught by a pendulum of mass M. After the collision, the pendulum swings up by an angle θ. Using the size of this angle, and some basic physics, we can figure out the initial speed v₁.

But we need to break the action into two steps. First, the projectile collides with the pendulum. Because the two stick together, this must be an inelastic collision.



  Q:  What physical principle can we use to derive the
            speed v₂ of the two objects after the collision?

Right. We should use conservation of momentum.



  Q:  Write an equation which gives the speed v₂ in terms
              of the initial speed v₁ and other quantities.

Now, in the second step, the arm of the pendulum (which carries the projectile inside it) swings up by some angle θ from the vertical. As a result, the center of mass of the pendulum-plus-projectile rises by a distance h.



  Q:  What physical principle can we use to derive the
            height h of the center of mass?

Right. We should use conservation of energy.



  Q:  Write an equation which gives the height h in terms
              of the speed v₂ and other quantities.

So, in order to determine the muzzle velocity v₁ of the projectile, we need to work backwards.

use the measured angle θ to compute the speed v₂
use speed v₂ in order to determine the muzzle velocity v₁

Of course, if our measurements of θ, or any of the other quantities m, M, L, have uncertainties, then our result for the muzzle velocity will contain some uncertainty, too.

Make a copy of this spreadsheet and fill it with your results

Not sure how to deal with the uncertainties?

a brief GENERAL guide to using uncertainties in calculations
a SPECIFIC example of using uncertainties in the ballistic pendulum; the numbers will be different than yours, but the method should be the same

Part 1 of example
Part 2 of example
Part 3 of example