
Video of marbles in slow motion from The Beauty of Slow Motion
At the start of this class, we defined a set of variables to describe the motion of objects: position, velocity, and acceleration. Although we didn't emphasize it at the time, these quantities pertain to LINEAR motion: bulk movement of an object from one location to another.

Video of marbles in slow motion from
The Beauty of Slow Motion
For the next few weeks, we will investigate a different sort of motion: ROTATIONAL motion, in which the center of an object doesn't translate from one place to another, but during which its parts do move in circular paths around its center.

Video of windmill courtesy of
Jonathan Cutrer
In order to describe this new sort of motion, we will need to use a new set of variables. Each of the LINEAR quantities has an ANGULAR counterpart. Note that both the symbol and the units are different.
In the linear world, displacement describes the how far some object is from a reference point. In the angular world, we use angular displacement to describe how far an object has rotated from some reference orientation.
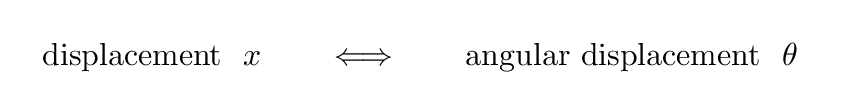
Q: What are the units of angular displacement?
The angular velocity of an object is the rate at which its angular orientation changes with time. Note that the symbol for angular velocity is the Greek letter omega = ω, not a lowercase Roman double-u "w".
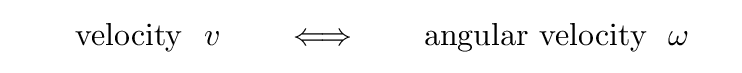
Q: What are the units of angular velocity?
In the linear realm, acceleration is the rate of change of velocity with respect to time. In the angular realm, angular acceleration is the rate of change of angular velocity with respect to time. Note that the symbol for angular acceleration is the Greek letter alpha = α, not a lowercase Roman letter "a".
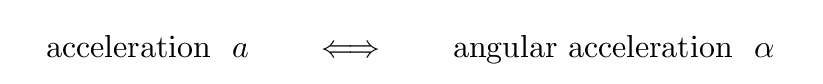
Q: What are the units of angular acceleration?
Physicists have defined the angular quantities so that they have exactly the same relative relationships with respect to time as their linear counterparts.
In the linear realm, velocity is the derivative of displacement (or position) with respect to time. Likewise, in the rotational realm, angular velocity is the derivative of angular position with respect to time.

In the same way, angular acceleration is the first derivative of angular velocity, and the second derivative of angular position.
