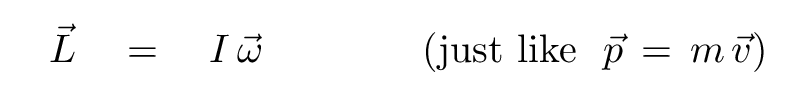
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
If an object is simply spinning around some axis within itself, then the angular momentum is the product of its moment of inertia around that axis with the angular velocity. This is just the rotational analog of regular linear momentum.
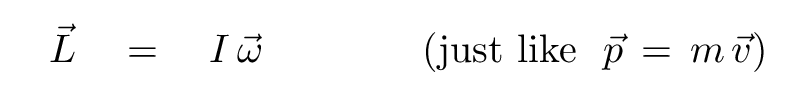
The DIRECTION of the angular momentum is simply the same as the direction of the angular velocity.
Let's look at a couple of examples.
Consider the Whirl-A-Kid ride at the county fair. Jack (mass = 40 kg ) and Jill (mass = 30 kg) are having a ball as the machine goes around and around and around.
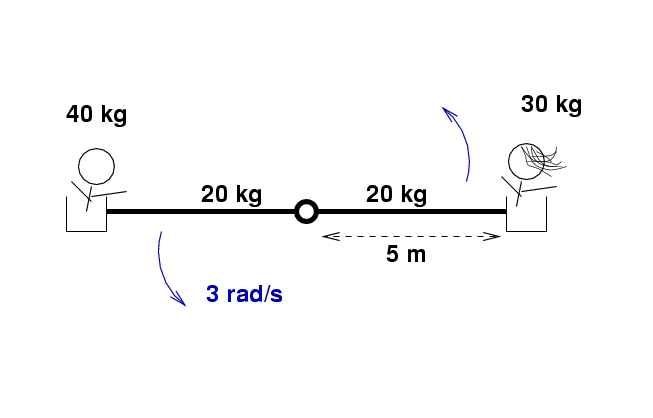
Q: What is the moment of inertia of Jack around the hub?
Q: What is the moment of inertia of Jill around the hub?
Q: What is the moment of inertia of each arm around the hub?
Q: What is the total moment of inertia around the hub?
Q: What is the total angular momentum around the hub?
Screenshot from a DVD copy of GoldenEye.
Image copyright for the film is owned by the Danjaq, L.L.C. &
United Artists Pictures.
The pretty spiral pattern around the muzzle's exit hole are grooves cut into the barrel of a gun. Here's another example, from a 75mm artillery piece used by the French in World War 1.
Image from Wikipedia Copyright © 2006 Med
Bullets which come out of a rifled barrel have grooves cut into them, like this one:
Image courtesy of
Stretcher Bullet Pictures
Q: Why put spin on a bullet?
Photo of Smith and Wesson .357 courtesy of
Wikipedia and Shotgun
Photo of ammunition (JSP on left) courtesy of ReconTonto and
Wikipedia Commons
Let's look at one particular example: a .357 Magnum revolver firing a Winchester 158 grain JSP bullet. We'll make a few approximations.
Q: What is the moment of inertia of the bullet around its long axis? Q: What is the angular momentum of the bullet around its long axis in flight? Q: What fraction of the total kinetic energy of the bullet is rotational KE?
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
