Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
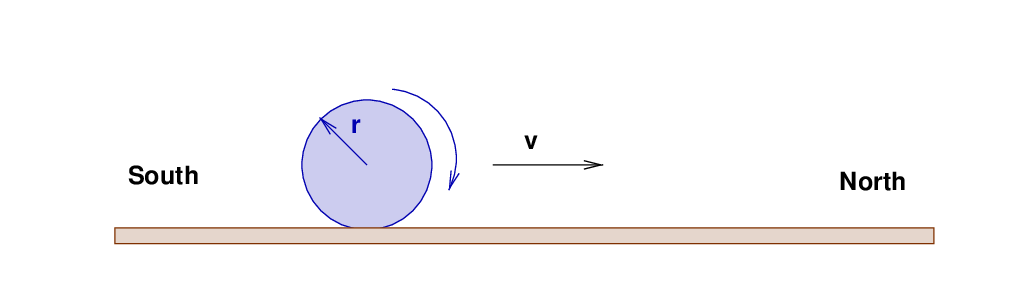
Oh, no! A giant rolling pin has escaped from the Culinary Zoo and is creating havoc! It is rolling North down Main Street, flattening citizens as it goes.
The pin is a giant cylinder of radius r = 3 m and length L = 10 m, with mass M = 2.4 x 106 kg. It rolls at a speed of v = 10 m/s to the North, too fast for most humans to escape.
Q: What is the moment of inertia of the rolling pin?
Q: What is the angular momentum of the rolling pin?
(provide a value, units, and direction)
Fortunately, the local lumberjacks spring into action. They drive their lumber truck after the pin, following it to the North, and hold a big log of mass m = 2000 kg so that it sits on top of the rolling pin. The coefficient of friction between log and pin is mu = 0.8.
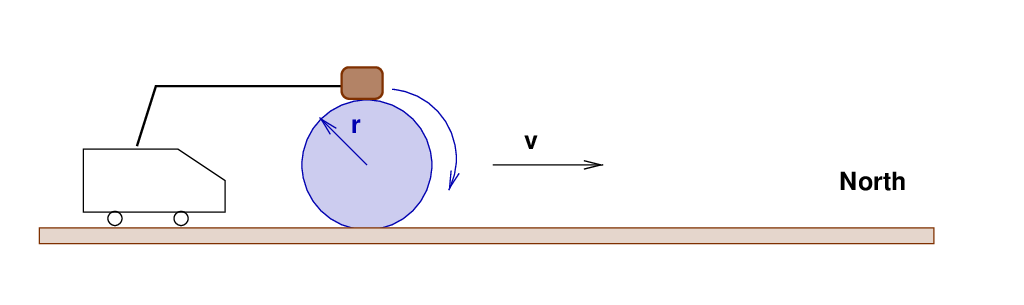
Q: What is the force of friction between log and pin?
(provide a value, units, and direction)
Q: What is the torque on the pin due to friction?
(provide a value, units, and direction)
Q: How much does the angular momentum of the pin change each second?
Q: How long will it take for the lumberjacks to halt the pin?
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.