Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
It turns out that there is a second way to compute the angular momentum of an object. Our first method required that the object be spinning around its own axis. This new method allows us to compute the angular momentum of an object which is moving around some rotational axis at a distance.
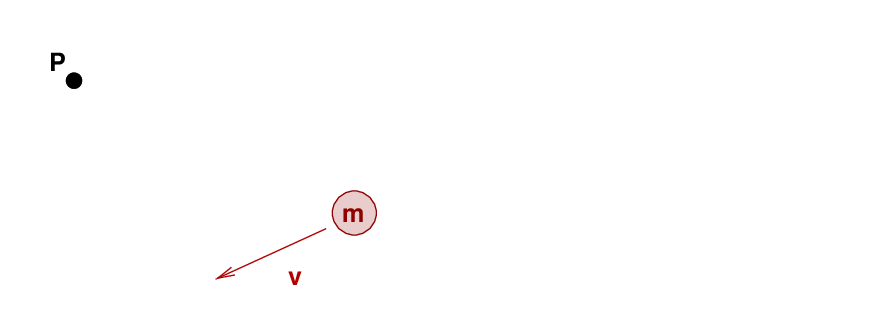
Consider an object of mass m moving with some translational velocity v. We are interested in the object's angular momentum around the point P.
In order to compute the angular momentum of this object around that point, we need to define a radius vector reaching from the axis to the object ... and then apply the cross product.
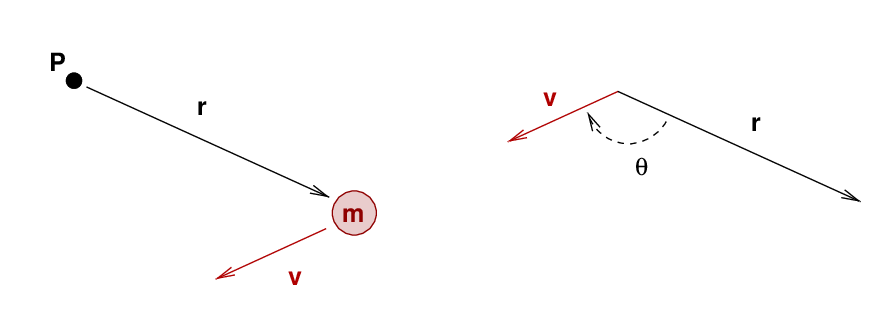
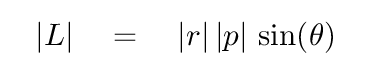
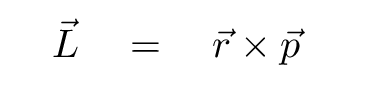
The DIRECTION of the angular momentum is given by the same right-hand-rule we use for the cross product.
Let's look at an astronomical example:
The Earth and Jupiter orbit the Sun. The Sun rotates around its own axis.
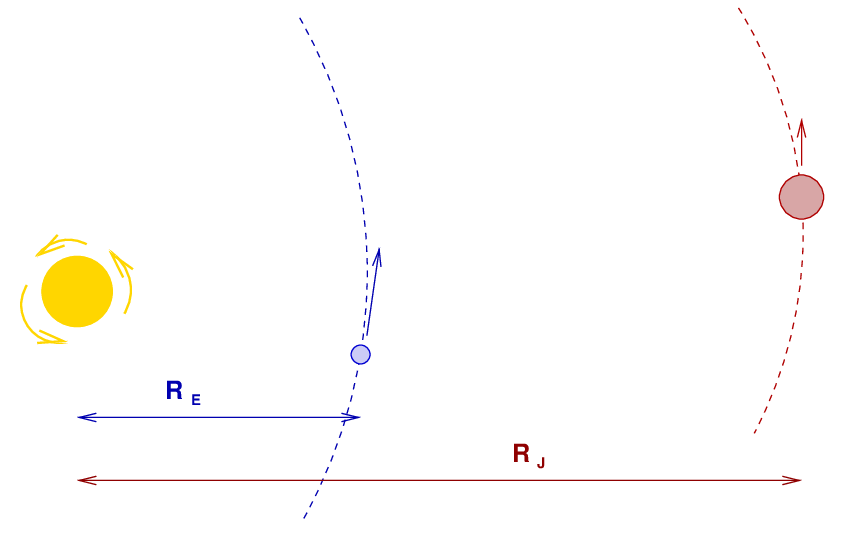
Body Mass Period Radius Orbital radius
(kg) (m) (m)
----------------------------------------------------------------------------
Sun 1.99 x 1030 1 month 6.96 x 108 ---
Earth 5.98 x 1024 1 year ---- 1.50 x 1011
Jupiter 1.90 x 1027 11.85 year ---- 7.78 x 1011
----------------------------------------------------------------------------
Can you determine the magnitude and direction of
Q: The Sun's spin angular momentum around its own axis?
Q: The Earth's orbital angular momentum around the Sun?
Q: Jupiter's orbital angular momentum around the Sun?
Q: Where is most of the angular momentum in the solar system?
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.