Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
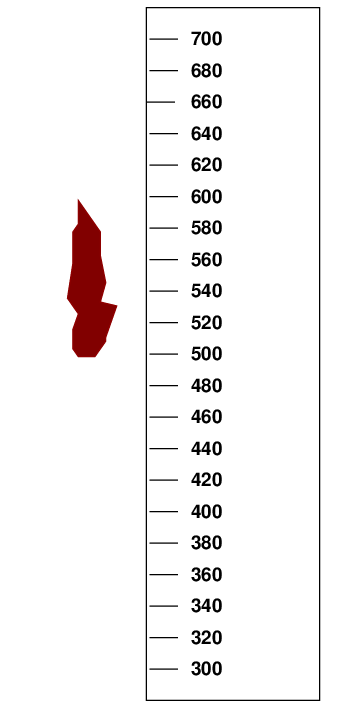
Joe the civil engineer checks the level of the Mississippi just outside of town. The rains are coming, and the people need to know whether a flood is possible. He looks at a rod which is stuck in the river bed, and notes the location of the mark left by the previous flood's waters. It's sort of smudge, which is hard to define precisely.
Q: What is the location of this smudge on the scale (marked in cm)?
Could it be 510 cm?
Could it be 570 cm?
Could it be 460 cm?
Could it be 630 cm?
Q: How many digits can you write which you are SURE to be correct?
Right. It's pretty sure that the first digit of the answer is "5", but after that ... the next digit could be "2", or "4", or "6", or just about anything. So, in this case, there is just one significant digit.
height = 500 cm = 5 m
Joe walks along the bank for a short distance, until he finds another rod. This one's mark is less smudged and easier to read.
Q: What is the location of this smudge on the scale (marked in cm)?
Could it be 520 cm?
Could it be 500 cm?
Could it be 560 cm?
Could it be 630 cm?
Q: How many digits can you write which you are SURE to be correct?
In THIS case, the first digit is definitely a "5". The second digit is almost definitely a "2". Therefore, we are justified in writing this measurement with two significant digits.
height = 520 cm = 5.2 m
Joe's partner points to a third rod, which is located on the other side of the river. When they retrieve it, they find a very precise mark.
Q: What is the location of this smudge on the scale (marked in cm)?
Could it be 520 cm?
Could it be 524 cm?
Could it be 522 cm?
Could it be 528 cm?
Q: How many digits can you write which you are SURE to be correct?
Here, the first two digits are definitely "52". The third digit is pretty certainly "2". Therefore, we are justified in writing this measurement with three significant digits.
height = 522 cm = 5.22 m
Is there a connection between +/- uncertainties and significant figures? Yes, indeed. For example, how many students at RIT are on campus today?
N = 12,439 +/- 338
This number could be as big as 12,777, or as small as 12,101.
12,101 < N < 12,777
The first digit -- 1 -- doesn't change. The second digit -- 2 -- doesn't change. But the third digit could be 1, or 2, or 3, or 4, or 5, or 6, or 7. So, if we write the number N using significant digits, we should write
N = 12,000
since these are the only digits we are SURE are correct.
Significant figures are like viruses: they infect any numbers they touch. If you combine two quantities, then the number of significant digits in the result is equal to the SMALLER of the number of significant figures in the input values.
For example, if you add two values, one with 5 significant figures and another with 1, then the result will have only 1 significant figure.
Can you write the answers to the following combinations?
83 meters/sec * 1.459 seconds =
0.05 kg / 250 cubic meters =
$12 / hour * 2.000 x 103 hours =
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.