
Image of the "Tokai Challenger" courtesy of Wikipedia
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Your friend Herbie lives in Buffalo, a distance d = 75 miles from your home in Rochester. On a nice Saturday, you decide to drive to his place for a visit.
But instead of the usual car, you decide to make the trip in a solar-powered racer!

Image of the "Tokai Challenger"
courtesy of
Wikipedia
When you hit the road at 6 AM, the Sun is barely up above the trees, and your car barely creeps forward. But as the Sun rises, the car goes faster. In fact, the speed rises in a very regular manner:
6 AM v = 0 mph
7 AM v = 10 mph
8 AM v = 20 mph
9 AM v = 30 mph
10 AM v = 40 mph
... and so on. In fact, you can describe the speed of the car in the following manner, where t is the time in hours since your trip began.

Q: How long does it take to reach Buffalo at this constant acceleration?
Which of the 1-D kinematic equations is the best choice here? I think this one:
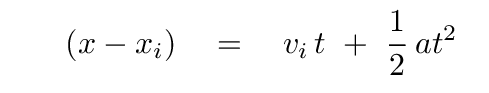
Let's replace the general terms in the equation with our variables: the distance d from Rochester to Buffalo is the displacement, and the initial velocity is zero, so we can write
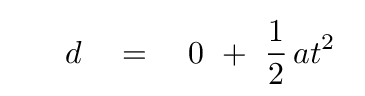
Now we use algebra to move the quantity for which we'll solve -- the time of the trip, t -- to the left-hand side; and compute!
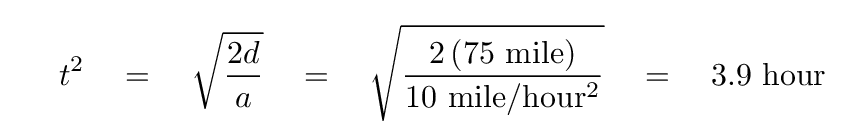
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.