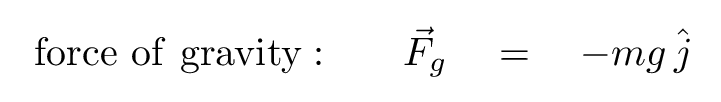
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
You have seen previously the connection between a force and the potential energy associated with it: give me a force, and I'll show you the potential energy.
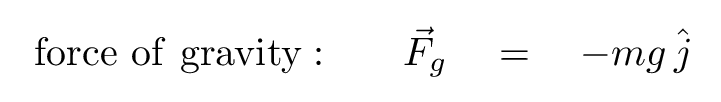
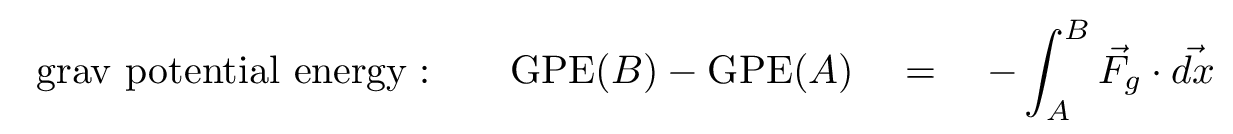
For example, Joe works at a construction site, where a new building has been only partially finished. The building is W = 200 m wide and H = 50 m tall. Joe (who has mass m = 60 kg) is standing at the lower left corner of the building.
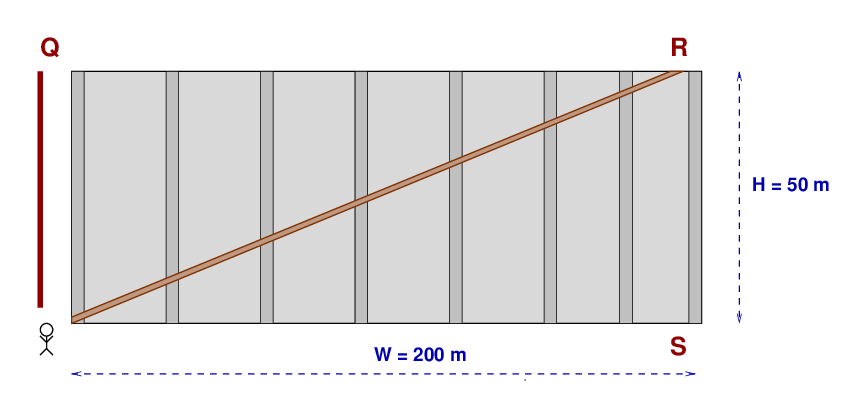
Q: What is the change in Joe's GPE if he climbs the rope to point Q? Q: What is the change in Joe's GPE if he walks up the ramp to point R? Q: What is the change in Joe's GPE if he walks along the ground to point S?
So going from a force to the associated potential energy isn't so bad -- one simply needs to integrate the force over the displacement from start to finish.
But can we reverse the process? Suppose someone tells us about the potential energy at a number of locations in some region of space -- can we figure out the force which will act on an object moving through that space?
Yes! If we need to INTEGRATE to go from a force to its associated energy, then ...
Q: ... in order to go from a potential energy to a force,
we need to perform what mathematical operation?
Exactly. We need to TAKE THE DERIVATIVE. Formally speaking, the force F associated with some potential energy PE is given by this partial derivative:
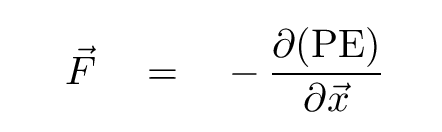
What's a partial derivative? In this case, it's a special sort of operation, which
For basic purposes, one can think of it in a simple way: how much does the PE change as Joe takes a step in some direction?
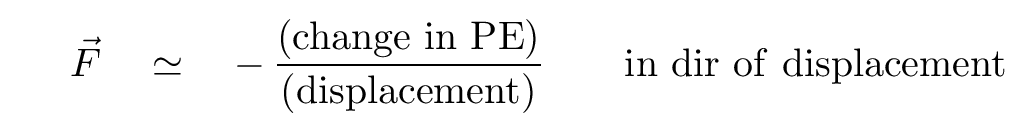
Consider three little steps Joe might take along his journeys to each of the three destinations.
Q: What is Joe's change in GPE for each step?
Q: What is Joe's displacement for each step?
Q: What is the force of gravity on Joe in the direction of motion
for each step?
Carol studies the properties of atoms in a crystal. She notices that if she displaces one particular carbon atom from its natural location in the crystal lattice, its "crystal potential energy" increases. In fact, she measures that energy to have the following form:
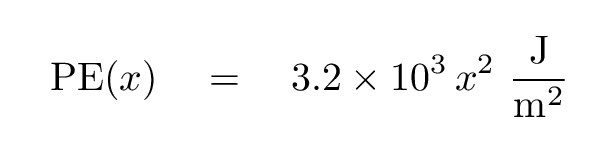
Q: What is the force on this atom if it is displaced by x = + 0.1 nm? Q: What is the force on this atom if it is displaced by x = - 0.1 nm?
The forces are
In other words, displace it to the right -- and the force pulls it back to the left; displace it to the left, and the force brings it back to the right. This sort of force is sometimes called a "restoring force", because it always acts to "restore" the object to an equilibrium position.
The graph below shows the potential energy of the atom in a crystal as a function of the displacement of the atom from its normal position.
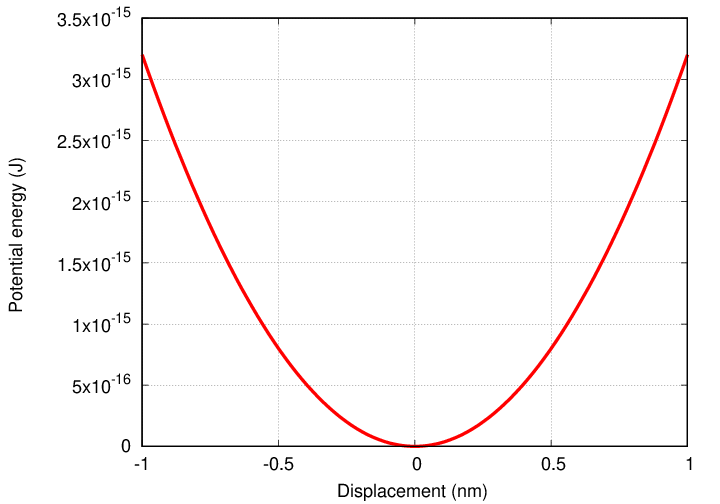
Examining a graph of potential energy as a function of position can reveal some very useful information.
But in some cases, the potential energy graph might have a different shape. The graph below shows the gravitational potential energy of an automobile along a road with dips and rises.
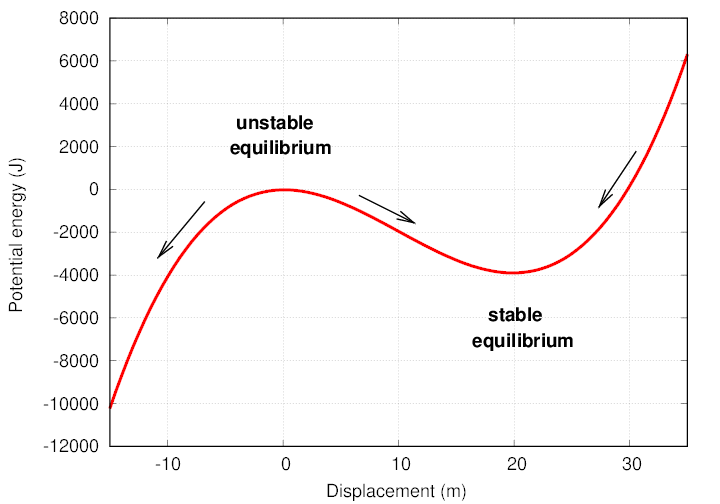
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.