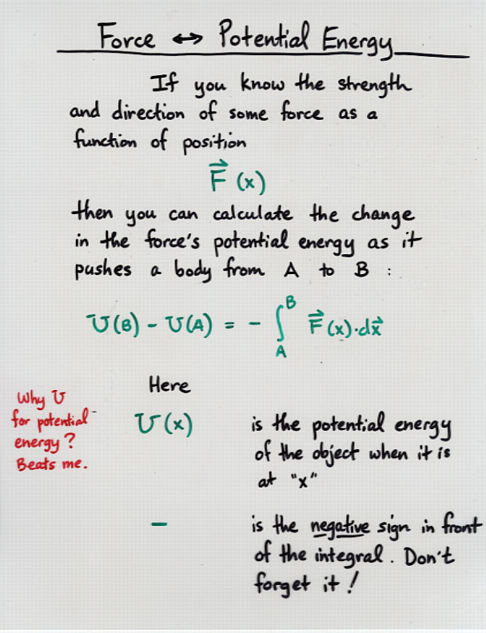
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
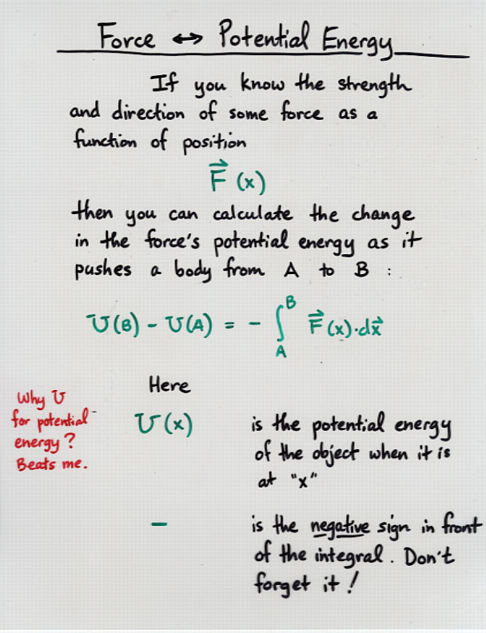
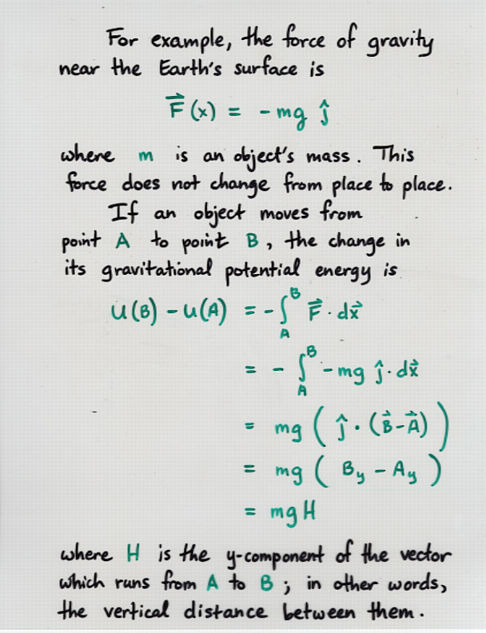
Not all forces have associated potential energies. For example,
We call forces which do have associated potential energies conservative forces. One way you can recognize a conservative force is to take an object on a round trip and see what happens to it.
Conservative Non-conservative
----------------------------------------------------------------------
Examples gravity friction
spring force air resistance
electricity water resistance
Work done by
force during
a round trip zero negative
(closed path)
Does it have
a potential energy? yes no
----------------------------------------------------------------------
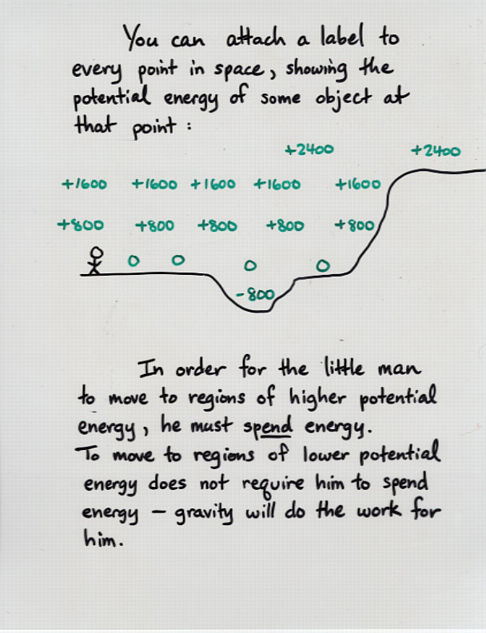
Here's a somewhat more sophisticated map showing potential energy -- electric potential energy in this case -- as a function of position on a piece of paper.
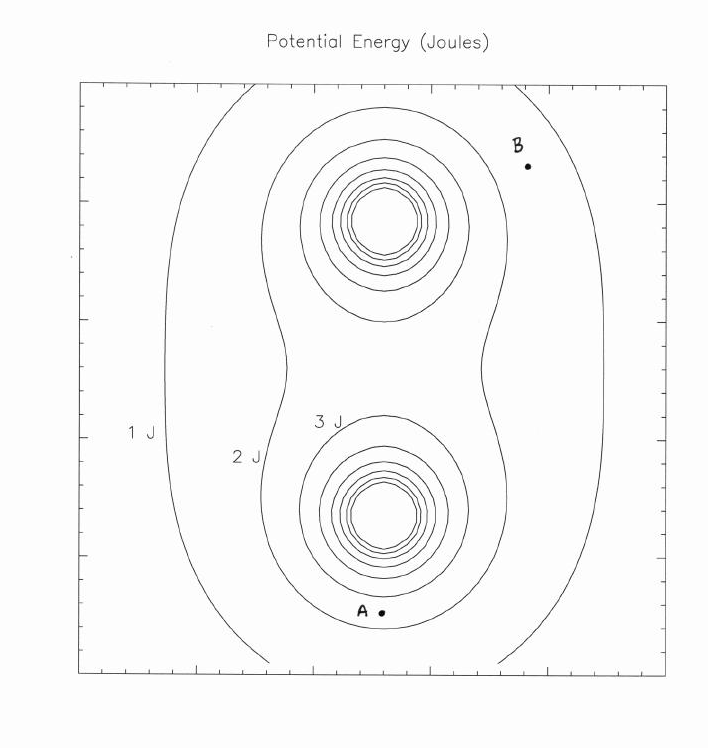
Q: What is the change in potential energy
per meter at location A, if one
moves to the right on this map?
Q: What is the change in potential energy
per meter at location A, if one moves
upward on this map?
Q: In which direction is the change in potential
energy largest at point B?
Q: What is the size of the electric force at point B?


Q: What is the size, and direction, of the
force on a particle at point A?
Express this force in unit-vector notation.
Q: At what locations is the total force on
a particle zero?
We call locations at which the net force on a particle equilibrium points. In theory, if you place a particle at one of these locations, since it feels no force, it should not accelerate -- or move.
But not all equilibria are created equal. Suppose you move the particle just a TEENY LITTLE BIT away from the point of equilibrium. What happens next?

Q: Are there any stable equilibrium points
on the map of electric field?
Q: Are there any unstable equilibrium points
on the map of electric field?

If you are interested in orbits and rockets and space travel, you might read about the important case of Lagrangian points in the Earth-Moon, or Sun-Earth, or Sun-Jupiter, systems. Things get a little more complicated --- but useful! -- when one adds rotation to the mix....
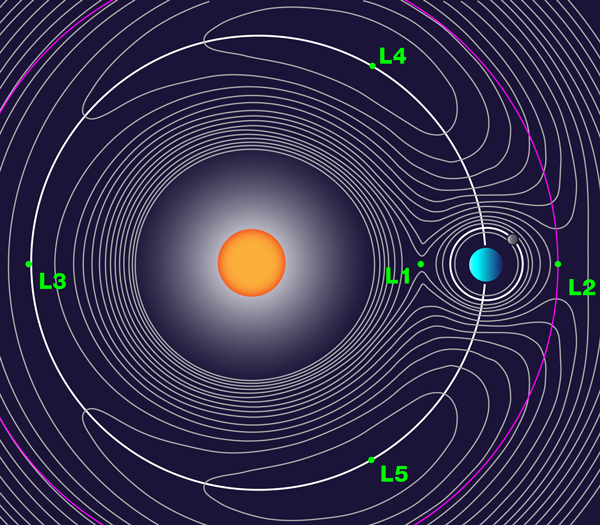
Image courtesy of
The American Physics Society
Suppose that in some region of space, the potential energy U (measured in Joules) is a function of position (x, y) (measured in meters) like this:
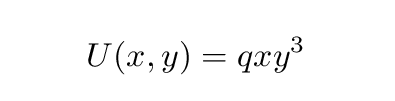
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.