Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
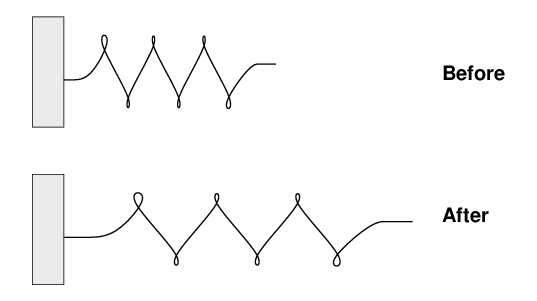
Joe finds a spring in an old junkyard. It looks pretty stiff. He attaches one end to a wall, leaving the right end free. When the spring is at rest, its length is L(rest) = 1.5 m.
Joe then pulls on the right end with a force of F = 400 N. The spring stretches, so that its new length is L(stretched) = 1.8 m.
Q: What is the force constant k of the spring?
Joe gets risky. He hangs the spring vertically from the ceiling, then climbs up on top of a bookcase, next to the spring. He grabs onto the bottom of the spring, and then steps off the bookcase.
Q: Just as his foot leaves the bookcase, what
is Joe's kinetic energy?
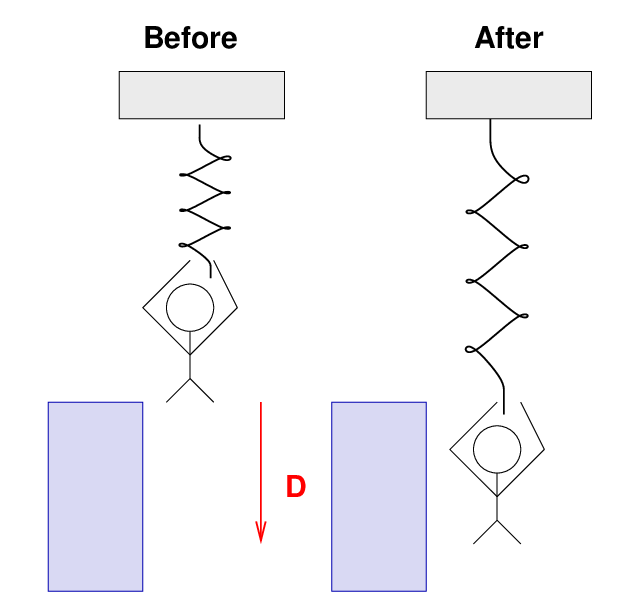
Joe is an ordinary guy of mass m = 60 kg. Joe starts to fall downward, and the spring begins to stretch.
Q: After Joe has fallen D = 0.2 m,
how much work has gravity done on Joe?
how much work has the spring done on Joe?
Q: At this moment, what is Joe's velocity?
Joe keeps falling, and the spring keeps stretching.
Q: At what distance D1 will the force of gravity
have the same size as the force of the spring?
Q: At this position, what will Joe's velocity be?
Joe keeps falling, and the spring keeps stretching.
Q: At what distance D2 will Joe's kinetic energy
finally become zero?
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.