Investigate the effect of elevation angle on projectile motion

Your job in this exercise is to watch very carefully as a ball is shot out of a gun, flies through the air, and lands on the floor. After you have analyzed its motion, you must predict where and when the ball will land when shot at a different angle.

Here's the basic setup:

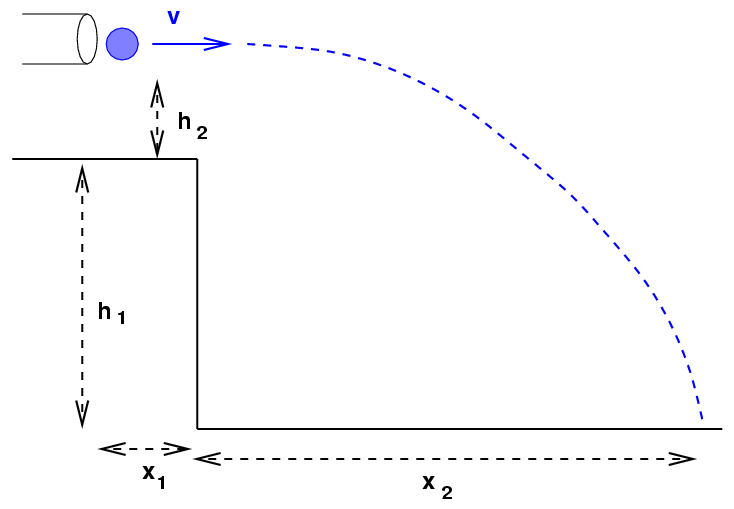
The two groups sitting at each table will share measurements during today's exercise. Each table will set up a single cannon on their table. Remove the barrel of the gun from the apparatus and re-set it onto the upper portion so that it is horizontal. Fire the cannon at its "medium range" setting. Measure the time of flight in each case. Make three trials and determine the average distance the ball travels. Each group independently must

1. using the height H (= h1 + h2) and total length L (= x1 + x2), determine the speed v at which the ball leaves the cannon.

2. compute the uncertainty in the initial speed v.

3. calculate the time of flight t of the ball. Does it match your measurements? Discuss.

4. Now, suppose we change the angle of the barrel to theta = 65 +/- 3 degrees. Predict
   • the new distance the ball will travel
   • the new time of flight

     (use very approximate method for following -- ask instructor)

   • the uncertainty in new time of flight
   • the uncertainty in new distance

At this point, call an instructor over. Show him your work. When he verifies the information, you may continue.

5. Reset the cannon so that the angle of the gun is theta = 65 degrees. You will need to remove the gun barrel from the post and reverse it in order to tilt the barrel and fire upwards at 65 degrees.
6. Fire the gun three times; each time, measure the horizontal distance travelled and the time of flight.

7. Does the actual horizontal range agree with your predictions within the uncertainties? If not, what do you think is the single largest reason for the difference? Be quantitative.

8. Does the actual time of flight agree with your predictions within the uncertainties? If not, what do you think is the single largest reason for the difference? Be quantitative.
9. Replace the gun barrel into its original, horizontal position on the other side of the post.

Copyright © Michael Richmond. This work is licensed under a Creative Commons License.