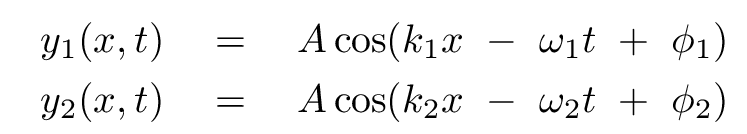
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Now let's consider two waves with the same amplitude, but DIFFERENT frequencies and wavelengths.
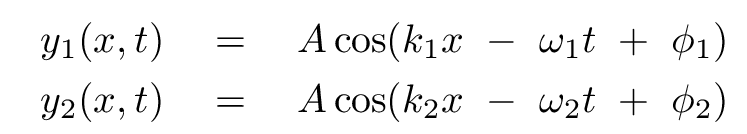
In general, this sum is a mess, with no simple and easy-to-understand results.
But if two frequencies (and wavelengths) are ALMOST the same,
First, though, let's simplify things a bit further.
That means that the equations for our waves, at the location of the observer, become
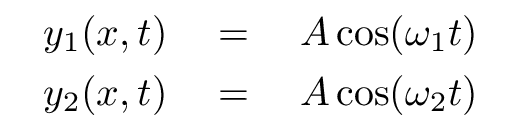
Once again, we turn to the trig identity
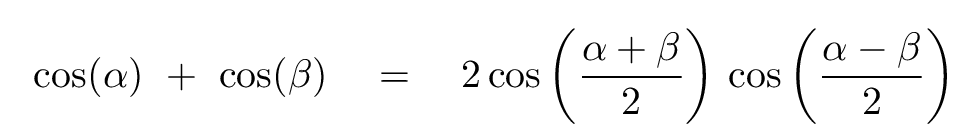
Q: Can you apply this identity to the sum of the two waves?
You should end up with something like this:
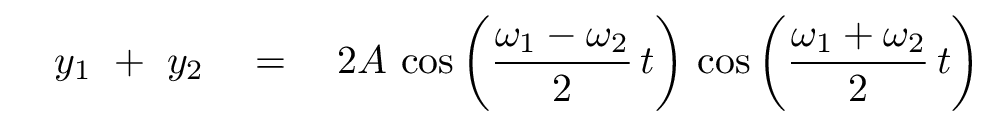
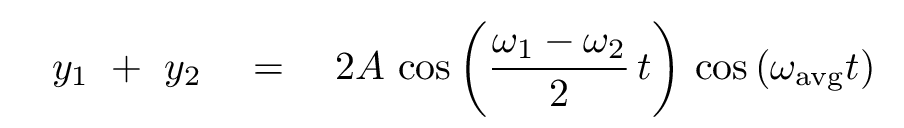
What does this mean? Take a look at the two waves: you can see them slowly growing out of phase with each other.
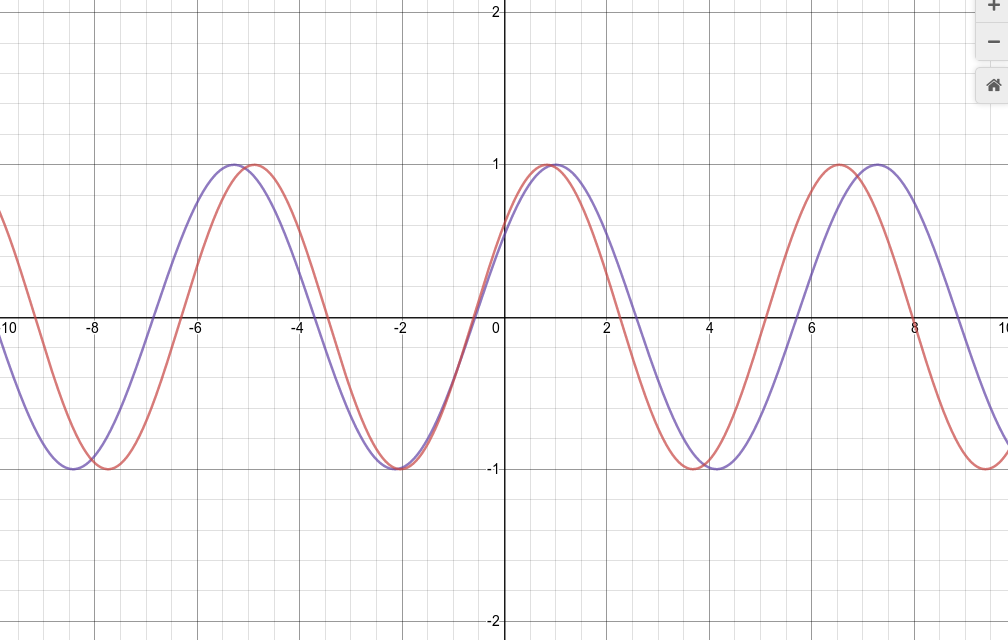
If we look over a larger range, we can identify the position where the two waves come back into phase with each other.
Now, add the sum of the two waves:
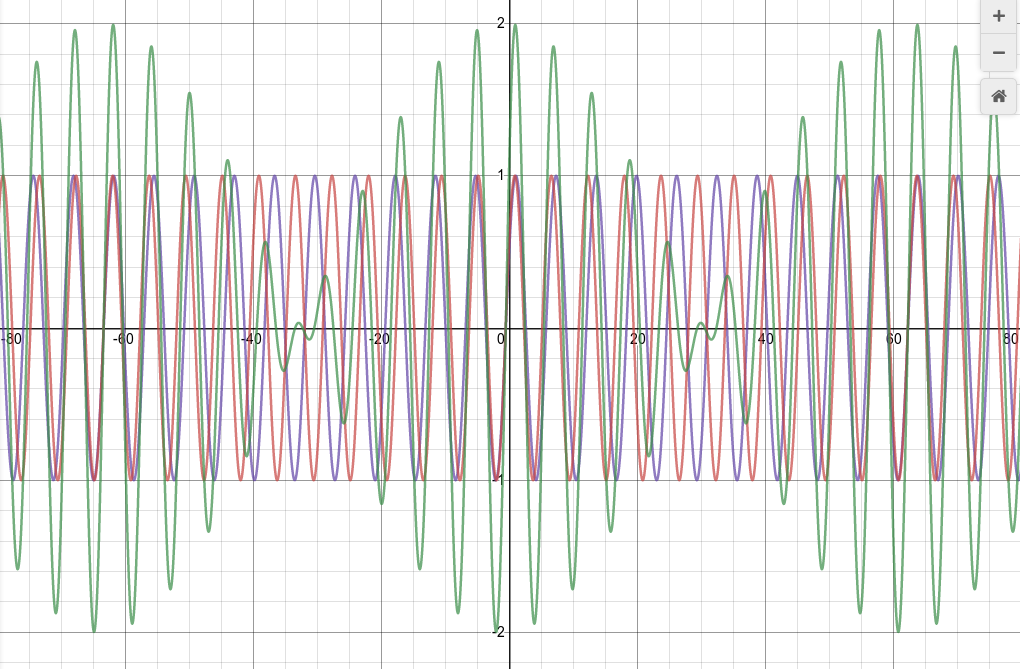
Maybe it's easier to see if we remove the input waves and just display the sum:
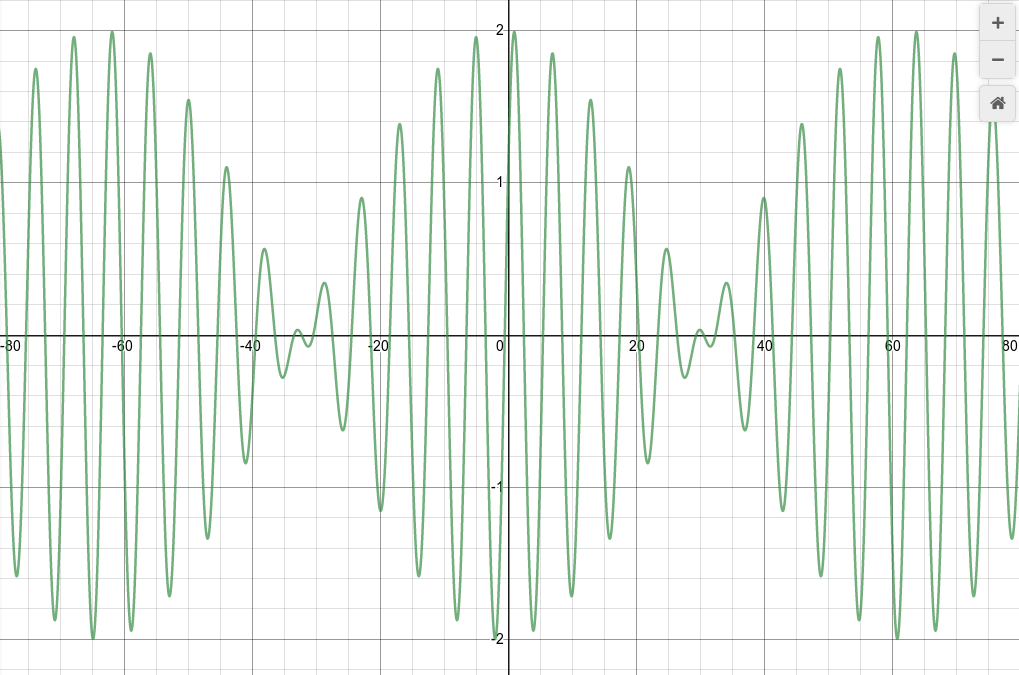
The superposition of the two waves has a form which combines two different waves:
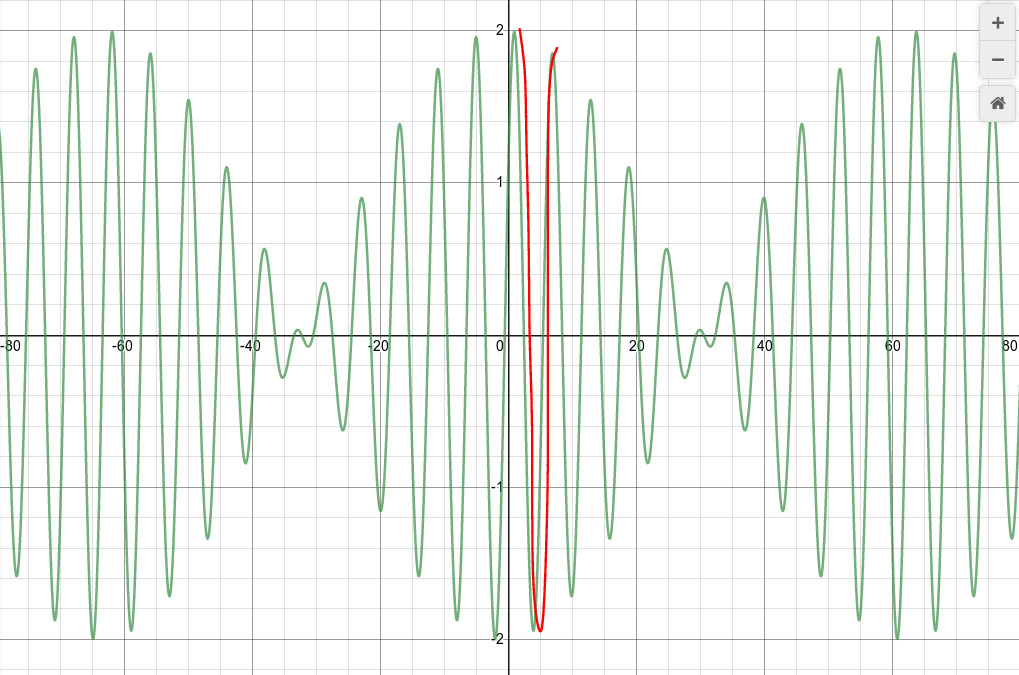
Note that the overall amplitude of the waves varies slowly with the envelope frequency: large, small, large, small, large, small. A person listening to these combined sound waves will hear
LOUD soft LOUD soft LOUD soft LOUD soft
If the difference in input frequencies is very small -- just a few Hz -- then the person will perceive a copy of input waves which oscillates in volume. We call these oscillations in volume beats.
One way to hear them is to run
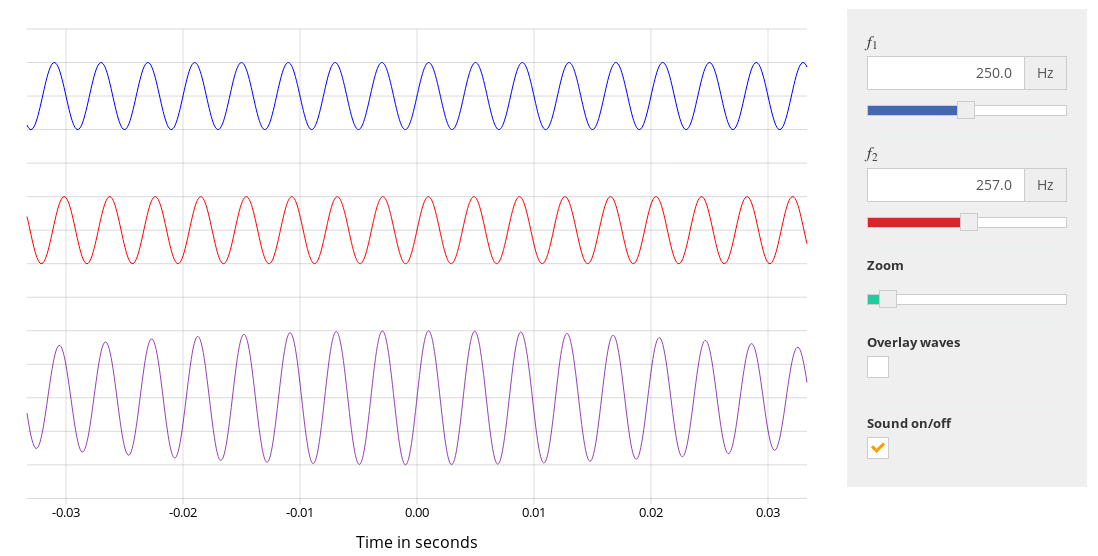
Image of the wave interference app thanks to
Academo.org
There's a subtle aspect to the beat frequency that a person will hear when listening to two sound waves which differ slightly in frequency. In order to explain it clearly, I'm going to switch notation slightly to match the most commonly used terms in music.
Musicians don't speak of the angular frequency (rad/s) of their notes; instead, they refer to the frequency in cycles per second, or Hertz (Hz). Let's do the same. Converting between the two is easy:
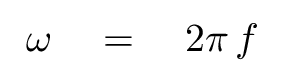
Our wave equations thus become
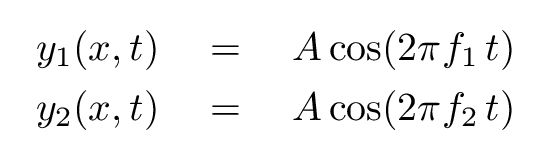
For a demonstration in class, let's adopt
The superposition of these two sound waves can be written
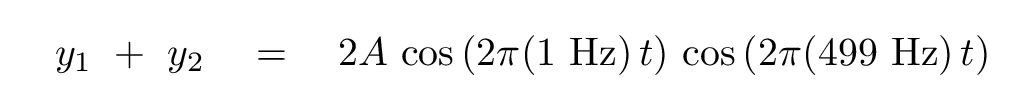
Listen to the result of this combination. The basic sound is a note of frequency 499 Hz, just as we expect. It sounds very similar to the two input sound waves.
But we can also hear beats.
Q: How many beats do you hear per second? Q: Does that match your expectations from the equation above?
Aha! You hear 2 beats per second, not 1. What's going on?
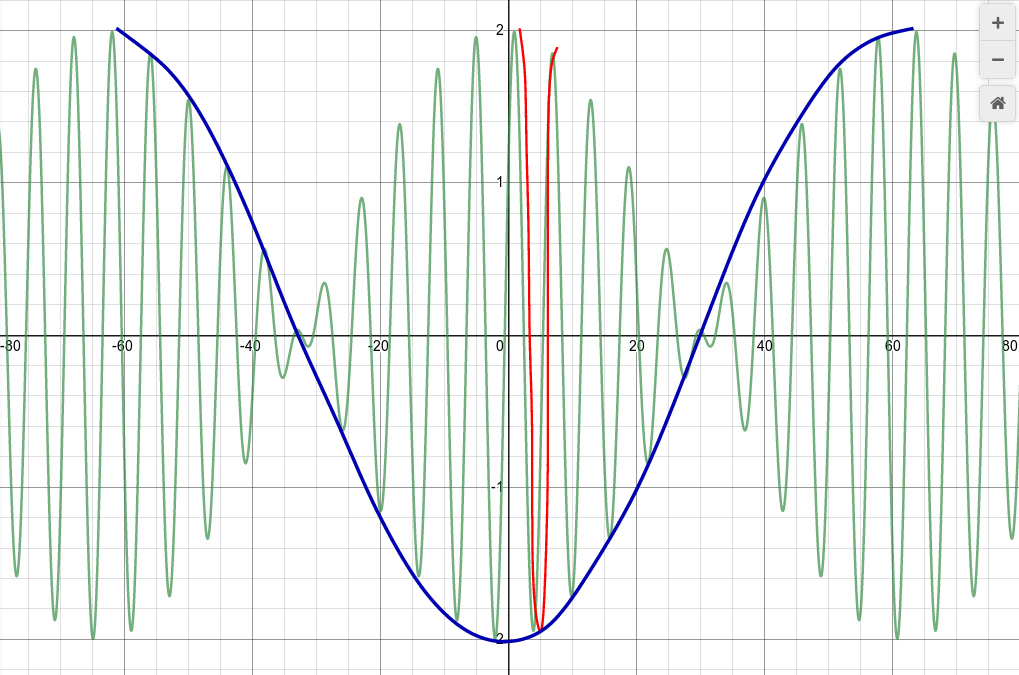
Go back to this picture of the combined wave:

Our ears perceive a "loud" sound whenever the combined amplitude is large and positive. Look carefully at the blue line, which shows exactly one cycle of the envelope wave. During that one cycle, the envelope varies from max-to-min-to-max again. But even when the envelope is at its minimum value, the combined wave does have a large amplitude.
Thus, we hear TWO loud "Wah-Wah" sounds during each cycle of the envelope wave.
In short, the frequency of the beats is twice as fast as the equation might suggest.
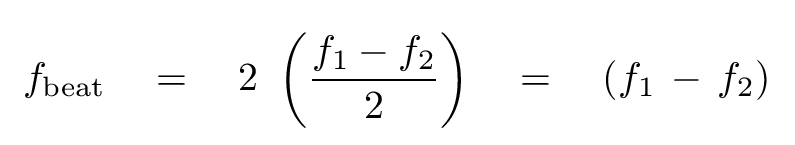
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.