 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Measure the speed of a wave
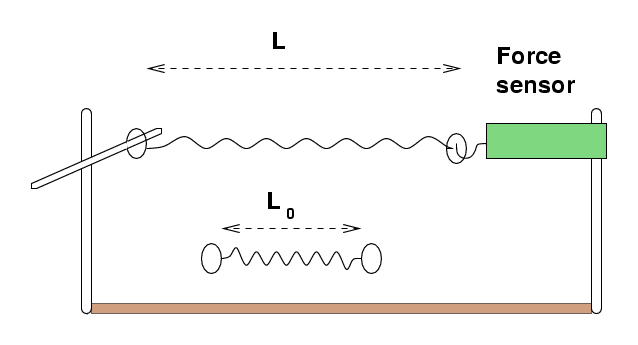
Your job is to measure the speed of a wave running along a spring.
How does the speed of the wave depend on the tension in the spring
and the linear mass density of the spring?
You'll have to work with all students at one table as a unit,
because we don't have enough equipment for each team of three students.
Set up a pair of vertical rods clamped to your table as shown above.
Clamp a short rod horizontally to one of the vertical rods;
you'll place the force sensor on the other vertical rod, but
only after you have calibrated it.
- Measure the rest length Lo of a little spring and its mass
m.
- Download the following file from the course web page by clicking
on the link and saving to your Desktop.
Double-click on the file to start LabPro running.
- Set the force sensor to its 10-Newton setting and calibrate it
with one of the heavy masses from the big cylindrical mass set.
- Pick 5 distances between 15 cm and 50 cm.
For each distance L,
- Arrange the rods so that when the spring is stretched
between the hook on the force sensor and the
horizontal rod, its length is L.
- Compute the linear mass density of the spring when
it is stretched to this length.
- Measure the static force of tension in the spring
- Gently pull together several coils near one end of the
spring, click the "Collect" button in LabPro,
and then release the spring. You should see a jagged
series of force pulses recorded.
- Measure the time it takes for the wave to travel back and
forth across the spring 20 times. Calculate the
speed of the wave
- Optional: determine the time constant for the decay
of the wave amplitude at each length.
You must now make two graphs.
- Make one graph with which you can compute the force constant
of the spring and its uncertainty.
- Use the formula you've learned today to compute the
theoretical speed of the wave along the spring at each of the
five stretched lengths.
Make a graph showing the actual speed of the wave
versus the theoretical speed.
Use this graph to answer these questions:
- Is there a linear relationship between the
theoretical speed and the actual speed?
- If so, write an equation of the form
actual speed = (const) * (theoretical speed)
and determine the value of the constant and its uncertainty.
- In an ideal world, the constant would have a value of 1.0.
Is your data consistent with this value,
within the uncertainties?
If you have time ...
Does the decay time of the wave depend on other
quantities, or is it constant during all your trials?
If it varies, describe the variation as quantitatively
as you can.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.

 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.

 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.