Properties of an elastic cord

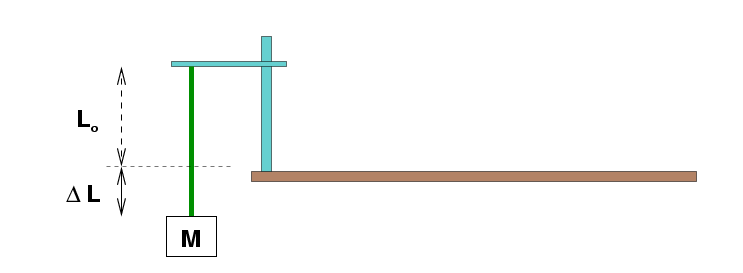
Investigate the properties of an elastic cord as it supports different amounts of weight.

1. Set things up so that a piece of cord of initial length L_o is hanging freely from a rod. Make the initial length at least 40 cm. Measure the diameter of the cord using calipers.
2. Hang at least six different masses in the range 300 g to 700 g from the cord. For each mass, measure the amount Δ L by which the cord stretches.
3. Make a neat table with your results.
4. Create two graphs with your data:
   1. Make a graph on which the slope of the line will show the spring constant k of the cord.
   2. Make a graph on which the slope of the line will show the Young's modulus E of the cord.
   On each graph, show clearly the range of masses over which the relationship is linear, and the range (if any) over which the relationship is NOT linear.
5. Use the linear portions of each graph to compute the spring constant k and Young's modulus E of the cord. Include uncertainties if you can.
6. I claim there is a theoretical connection between k and E that looks something like this:

                        (             )
                 k  =   ( something   )  *  E
                        (             )
   

   1. Based on the values from your graphs, what is the "something"?
   Call this the experimental result.
   2. Using theory and the defintions of spring constant and Young's modulus, what is the "something?" Provide it in symbols, in terms of some properties of the cord. Call this the theoretical result.
   3. Plug in the measured properties of your cord to the theoretical result. Does it agree with your experimental result?