Angular Momentum in the real world

Let's look at some examples of angular momentum in the real world.

When quarterbacks throw the football, they impart a spin with their fingers, so that the ball spins rapidly as it flies through the air. Football fans call a good pass a tight spiral.



      Q:  Why put spin on the ball?

Screenshot from a DVD copy of GoldenEye. Image copyright for the film is owned by the Danjaq, L.L.C. & United Artists Pictures.

The pretty spiral pattern around the muzzle's exit hole are grooves cut into the barrel of a gun. Here's another example, from a 75mm artillery piece used by the French in World War 1.

Bullets which come out of a rifled barrel have grooves cut into them, like this one:

Image courtesy of Stretcher Bullet Pictures



      Q:  Why put spin on a bullet?

Let's look at one particular example: a .357 Magnum revolver firing a Winchester 158 grain JSP bullet. We'll make a few approximations: that the bullet moves at its final speed throughout the muzzle, and that it follows the rifling grooves perfectly without slipping.

bullet leaves muzzle with speed v = 1235 fps
muzzle is rifled so that each twist requires d = 8.25 inches inside the barrel
bullet is a solid cylinder of length L = 1.29 inches, diameter D = 0.357 inches (hence the name of the gun), and mass m = 158 grains = 10.2 grams



      Q:  What is the moment of inertia of the bullet around
          its long axis?

      Q:  What is the angular velocity of the bullet around
          its long axis when it leaves the muzzle?

      Q:  What is the angular momentum of the bullet around its
          long axis in flight?

      Q:  What fraction of the total kinetic energy of the bullet
          is rotational KE?

The Hubble Space Telescope floats freely in space.



    Q: How can astronomers change its orientation 
       so that it points to some particular star?

Propellent might leave residue on the mirrors -- very bad. It would also be imprecise, since HST needs to make small movements accurate to about 0.1 arcseconds.



    Q: If there are 60 arcminutes in one degree,
       and 60 arcseconds in one arcminute,
       what is the angular precision required
       for HST, in radians?

The answer: use reaction wheels, which are simply pairs of disks mounted inside the telescope structure.

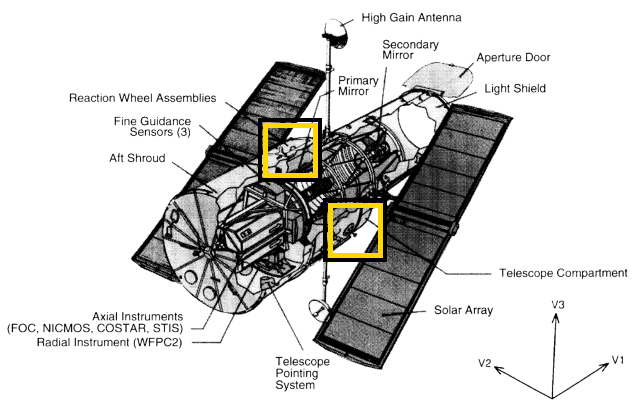
Each reaction wheel is about 40 cm in diameter and has a mass of about 40 kg. They are used in pairs.

Below are pictures of the reaction wheels aboard the Kepler space telescope . Click on each image to see a larger version.



      HST may be approximated as a cylinder with

         length   L = 13.3 m
         diameter D = 4.3 m
         mass     M = 11,100 kg

      At full speed, it can slew in angle at about
      the same speed as the minute hand on a clock.


      Q:  How fast must the reaction wheels be
          able to spin to cause this motion?
          
          Express your result in RPM.

It seems that in many cases, people use angular momentum to stabilize objects.