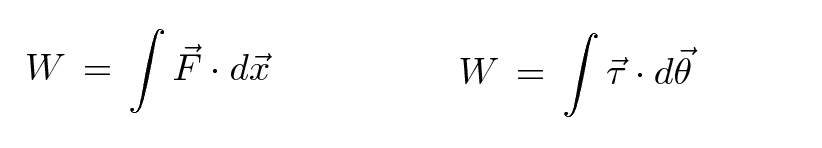
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
You've already seen some connections between the linear and rotational realms of physics; for example, the basic kinematic equations under constant acceleration are very similar to the kinematic equations under constant angular acceleration.
Here are a few more connections.
If you apply a force to an object as it moves over some displacement, you'll do some work on the object. The same is true if you apply a torque on an object as it rotates through some angle.
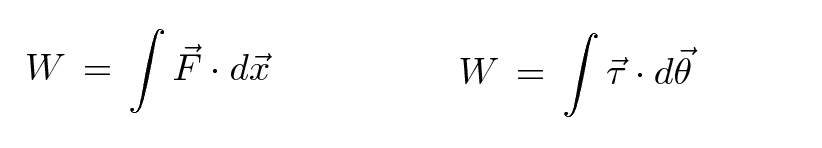
The Work/Kinetic-Energy Theorem states that the net work done an object is equal to the change in its kinetic energy. There's a similar theorem for rotational kinetic energy.
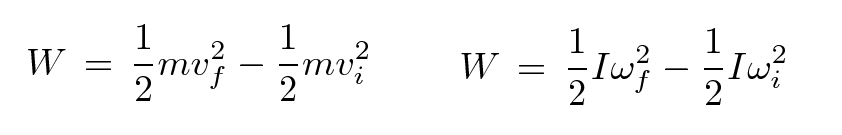
The instantaneous power supplied to a moving object by a force is the dot product of the force and its velocity. In the rotational world, a torque can likewise supply power to a rotating object.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.