Workshop 2A: Moments of inertia in theory and practice

Today you will examine the moments of inertia of two objects:

a thick ring
a pair of brass weights

Your job is to calculate the moments of inertia from theory, and also to determine the moments of inertia from an experiment in which these objects are spun around and around. The goal in the end is to see if the theoretical and experimental values agree to within their uncertainties.

Each group will hand in a report as homework, due at a future class meeting.

Tips for success:

use units of grams, centimeters, radians and seconds for all your measurements and your calculations. The results will be easier to write and discuss this way.
make two trials of all measurements involving the ring, and two trials of all measurements involving the rod
do not confuse the radius of the ring with its diameter; I did, and it took me three hours to figure out why everything was coming out wrong :-(
when I did this experiment, I found values within the following rough ranges
- linear accelerations between 0.1 and 10 cm/sec^2
- tensions between 3000 and 8000 gm*cm/sec^2
- torques between 3000 and 10,000 gm*cm^2/sec^2
- angular accelerations between 0.1 and 10 rad/sec^2
- moments of inertia between 500 and 60,000 gm*cm^2
If you find values outside these ranges, you may have an error in units ...

The ring, in practice

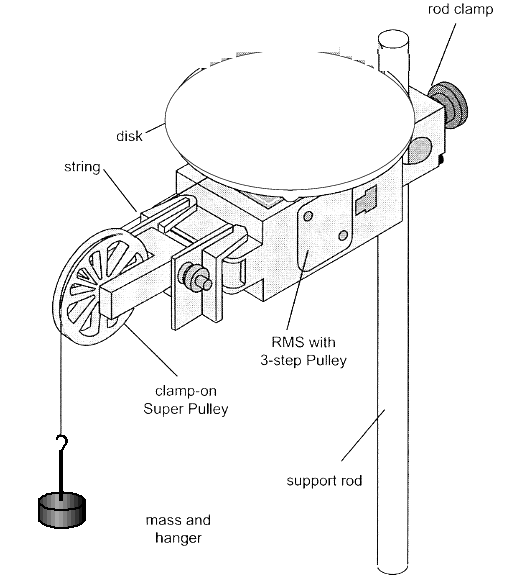
Attach the RMS with its 3-step pulley near the top of an aluminum rod, far above the level of the tabletop. Clamp the Super Pulley onto the RMS, on the side pointing away from the table.

You need to wrap a piece of black thread around the MIDDLE step of the 3-step pulley. Tie the thread in a knot anchored in the hole of the middle or largest step.

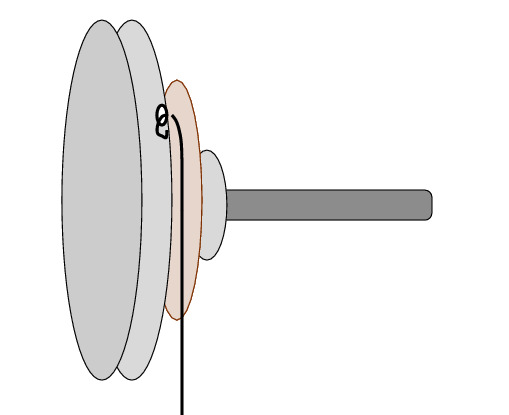
This would be a good time to measure the radius of this middle step. Use the vernier calipers with digital readout.

To the other end of the thread, tie a 5-gram plastic hanger from the blue mass set. Do NOT place any additional mass on the hanger.

Step 1:

Place an aluminum disk on top of the 3-step pulley; screw it into place.
Arrange your equipment so that the thread runs from the middle step, through the super pulley, and down to the hanger.
Adjust the super pulley so that the thread runs horizontally from the middle step to the super pulley.
Spin the disk gently to wrap the thread around the middle step, so that the hanger is just a few cm below the super pulley.
Measure the time it takes for the hanger to fall 10 cm. Then spin the disk gently to re-wrap the thread and pull the hanger back up near the top.
Repeat, so you have 2 trials total for a 10-cm drop.
Repeat, making 2 trials each for drops of 20 cm, 30 cm, 40 cm, 50 cm.

These measurements will allow you to determine the moment of inertia of (the RMS apparatus plus the aluminum disk).

Step 2:

Place a ring on top of the aluminum disk, so that the little bumps drop into the holes.
Make 2 trials each of the time it takes for the hanger to drop 10 cm, 20 cm, 30 cm, 40 cm, 50 cm.
Verify that the times are considerably longer than they were without the ring.

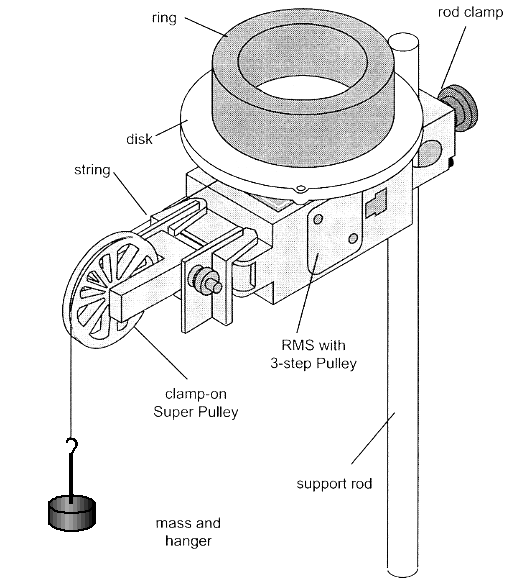
These measurements will allow you to determine the moment of inertia of (the RMS apparatus plus the aluminum disk plus the ring).

At this point, show your measurements to an instructor. Do not move forward until your values are checked and approved.

The brass weights, in practice

Step 3:

Remove the ring and aluminum disk. Attach the rod -- without the brass weights -- to the 3-step pulley. The rod should sit within a set of guides on opposite sides of the 3-step pulley.

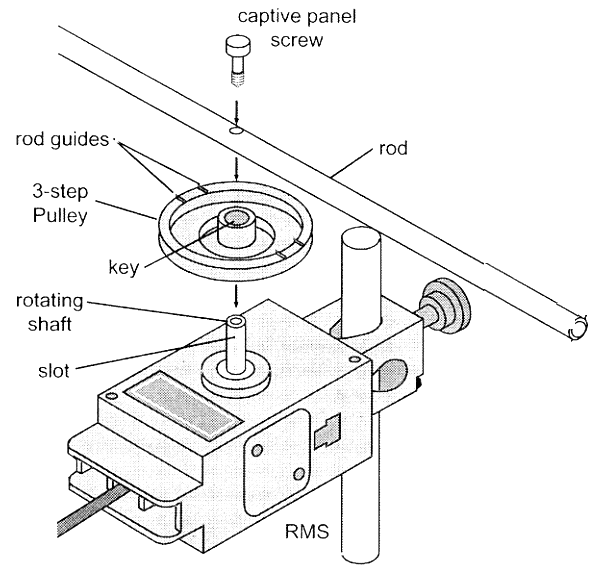
Make 2 trials each of the time it takes for the hanger to drop 10 cm, 20 cm, 30 cm, 40 cm, 50 cm.

These measurements will allow you to determine the moment of inertia of (the RMS apparatus plus the rod).

Step 4:

Attach the brass weights to each end of the rod, so that the outer face of each weight is flush with the outer end of the rod.

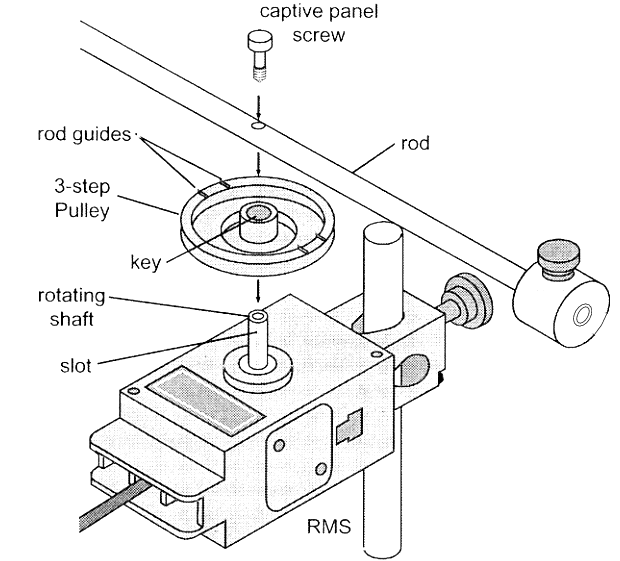
Make 2 trials each of the time it takes for the hanger to drop 10 cm, 20 cm, 30 cm, 40 cm, 50 cm. These should take a pretty long time each, so do only 2 trials each.

These measurements will allow you to determine the moment of inertia of (the RMS apparatus plus the rod plus weights).

At this point, show your measurements to an instructor. Do not move forward until your values are checked and approved.

Moments of inertia in theory

Measure the properties of the ring. Calculate its moment of inertia, and the uncertainty in that moment of inertia.

Place the two brass weights at the very ends of the rod. Measure the distance of each weight from the center of the rod, and the mass of each weight. Calculate the moment of inertia of the two brass weights alone (ignoring the rod's contribution), and the uncertainty in this moment of inertia.

You must reach this point by the end of the class period, with all the measurements you need. If there is still time left in the class, move forward with the calculations so I can help you!

Computing moments of inertia

For each of your datasets, you should make a graph of distance fallen (on the y-axis) versus time squared (on the x-axis). Compute the slope of the best-fit straight line to your data, and the uncertainty in that slope. Then calculate the linear acceleration of the hanger, in centimeters per second per second, plus its uncertainty.

If you know the mass of the hanger, and its acceleration, you can compute the tension T in the string; it will NOT be (mass) * (g), but something slightly different. Find the tension, and its uncertainty.

The thread pulls with this tension at the rim of the middle step of the 3-step pulley. Compute the torque exerted by the string around the axis of the 3-step pulley, and its uncertainty.

You can turn the linear acceleration of the hanger into an angular accelertion of the 3-step pulley. Do so. Determine the uncertainty in this angular acceleration, too.

Now, with both torque on the apparatus, and angular acceleration of the apparatus, you can for each case compute a moment of inertia -- and uncertainty. Do so.

We are interested in the moment of inertia of the RING ONLY, and the moment of inertia of the BRASS WEIGHTS ONLY. You have enough information now to figure out these quantities, and associated uncertainties. Do so.

The Big Result

Do the moments of inertia from theory agree with the moments of inertia you measured in the experiment? Do they agree within the uncertainties? Explain. Be quantitative.