The ballistic pendulum

A ballistic pendulum takes the horizontal motion of a ball and turns it into the swinging arc of an arm around a pivot:

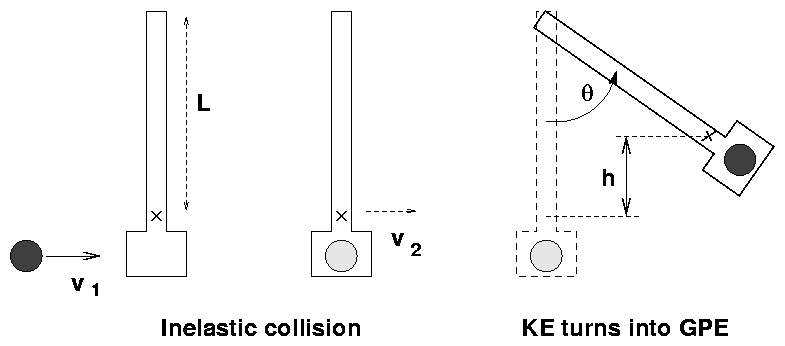
You can break the action into two pieces:

1. A ball of mass m moving at speed v1 slams into an arm of mass M. Use conservation of momentum in this completely inelastic collision to write an equation relating v1 to the velocity of the arm-plus-ball v2.
2. An arm with an initial speed swings up until it halts at an angle theta. Use conservation of energy to figure out the relationship between the speed of the arm-plus-ball, the angle theta, and the height h by which the center of mass of arm-plus-ball rises.

Your job today is to figure out the speed v1 with which the ball is fired from the catapult, by measuring the angle theta (and some other quantities).

• be very gentle with the swinging arm
• use the stuffing rods to push the ball into the catapult
• cock the catapult to the middle position -- two clicks. Do NOT go all the way to three clicks
• you will need to find the position of the center of mass of the arm-plus-ball
• watch the device when you fire the catapult. If it slides across the table, your measurements will be inaccurate: some of the momentum goes into the motion of the whole device, which you cannot measure
• try to estimate the uncertainty in each of the four quantities you need to measure

As you try to convert the uncertainties in the values you measured in class into an uncertainty in the initial speed v1 of the ball, you may find it useful to peruse

• this GENERAL guide to using uncertainties in calculations
• this SPECIFIC example of using uncertainties in the ballistic pendulum; the numbers will be different than yours, but the method should be the same
  • Part 1 of example
  • Part 2 of example
  • Part 3 of example

Copyright © Michael Richmond. This work is licensed under a Creative Commons License.