A block of mass M sits on a frictionless floor. Identical springs of force constant k are attached to its sides and to adjacent walls. The block is placed at x = 0, the springs are at their rest lengths, and everything is at rest.

1. If the block is displaced a distance x to the right, what will the net force on the block be?
2. If the block is then released, it will oscillate back and forth. What will the period of oscillation be?

Joe chooses a block with M = 1.5 kg and springs with k = 10 N/m each. He moves the block by 0.2 m to the left of the rest position and releases it at time t = 0.

3. Write an equation for the position of the block as a function of time.
4. What is the maximum speed of the block?

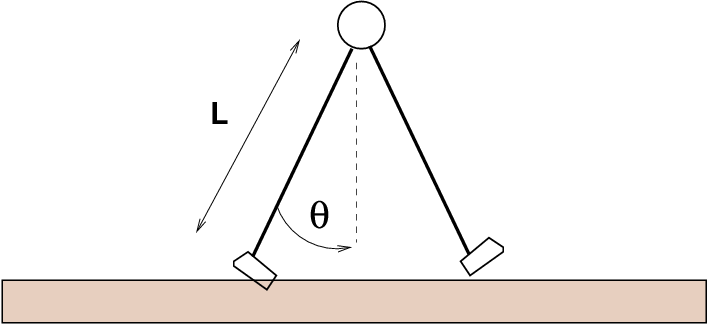
A very simple model for a walking creature involves two stiff legs of length L, each of which swivels by an angle θ away from the vertical as the animal takes steps. The basic idea is each leg swings like an ideal pendulum as the animal moves.

(Yes, this is a pretty bad model)

1. How long will it take the animal to make one complete pace, from "lift-right-foot" to "lift-right-foot" again?
2. How far forward will the animal move during that complete pace?

Now, let's pretend that all bipedal animals walk this way, and that each one swings its legs by an angle θ = 10 degrees.

3. How fast should an adult human with legs of length L = 1 m walk? Is this even close to correct?
4. How fast should a child with legs of length L = 0.5 m walk? Is this faster or slower than an adult human? Does this make sense?
5. How fast should an Allosaurus with legs of length L = 2 m walk? Is this faster or slower than an adult human?
6. Is there a general relationship between the size of an animal and its walking speed? If so, what is it?
7. How fast will an adult human walk on the moon? Assume that it is wearing a very lightweight and flexible spacesuit, so it moves in the same manner it would on Earth.