 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
As a wave passes through a medium, it transfers energy to that medium. For example, when a water wave enters a placid, still pool of water (low energy) it turns that pool into a choppy mess of ripples and waves (high energy).
Is there some way to quantify the energy transferred by the wave to the water?
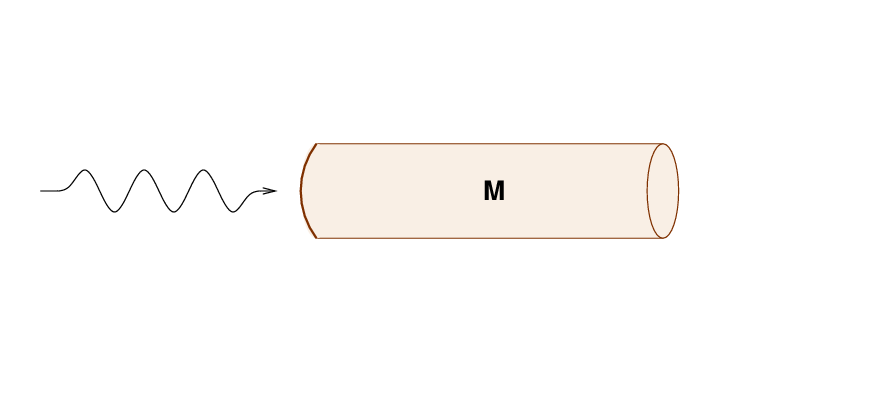
Let's start with a very simplified situation: a wave approaches a chunk of stuff of mass M which is currently at rest (brown = low energy):

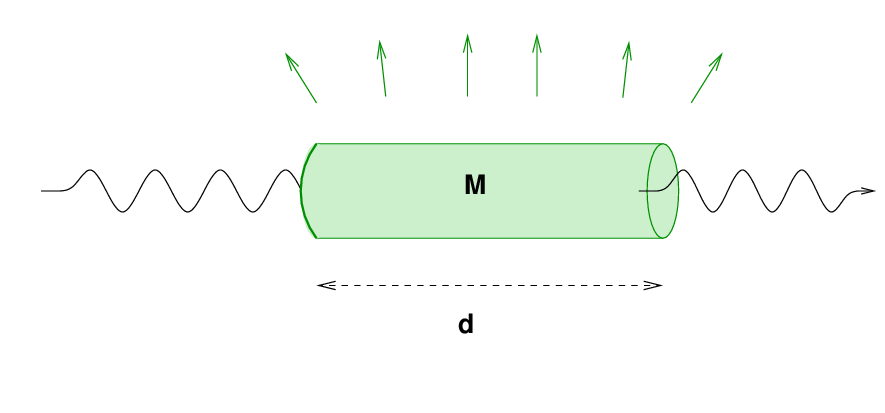
After the wave passes through the chunk, the material has been excited by the wave, and has lots of energy (green = high energy):
How much energy has the wave given to the particles of this chunk? Well, the kinetic energy of all the particles depends on their motion:
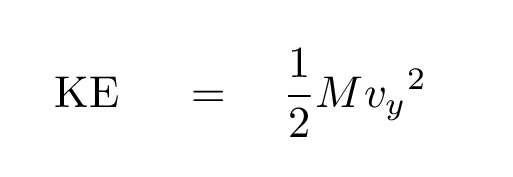
Q: Can you fill in the value of "vy" here?
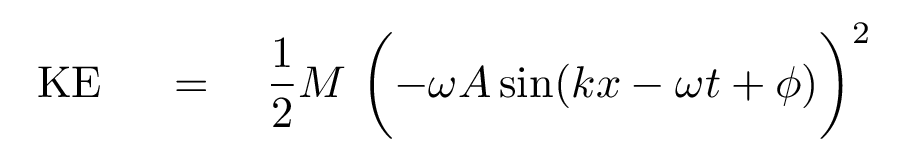
Now, at any given time, some of the particles will be moving rapidly, some slowly, some not at all: that's what the "sine" function means. But if we average over all the particles, we can find the average KE.
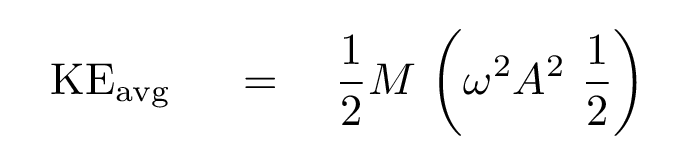
Okay, that gives us the average kinetic energy of the particles in this chunk of material. But they will also have potential energy, as they move away from their equilibrium positions. It turns out that the average potential energy is exactly equal in size to the average kinetic energy, for objects in SHM. Therefore,
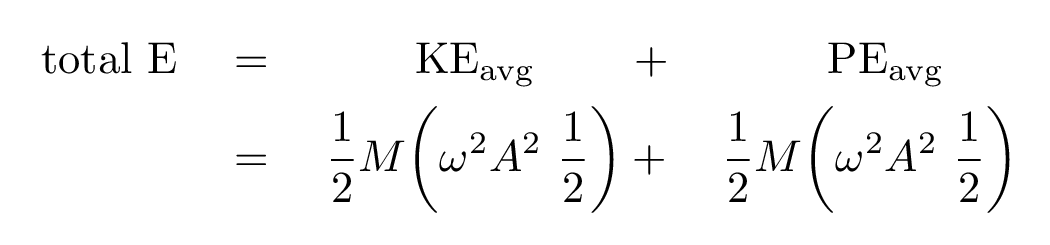
And so
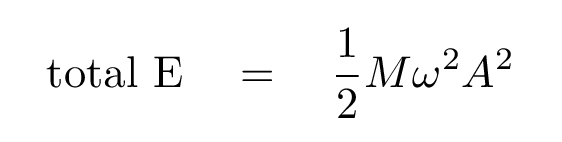
Note that the energy deposited in this chunk of material depends upon the total mass of the particles in the chunk. It is often useful to describe things in slightly different terms: in terms of power, which is the energy transmitted per unit time.
Look at the chunk. It has a mass M and a length d.

We can define its linear mass density μ as the mass per unit length:
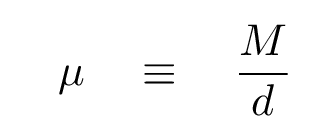
Now, the distance that the wave travels in some time interval t is simply the wave's speed v multiplied by the interval. So, the amount of mass disturbed by the wave during that time interval must be
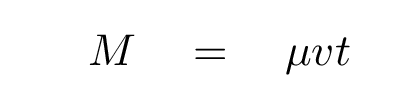
The total energy of this disturbed mass is simply
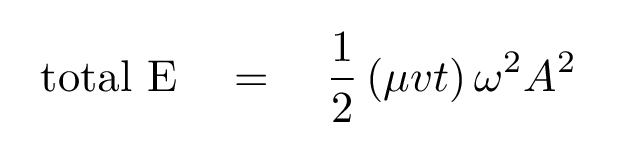
Q: Can you write an equation for the POWER transmitted to the
chunk by the wave?
Pretty simple, isn't it?
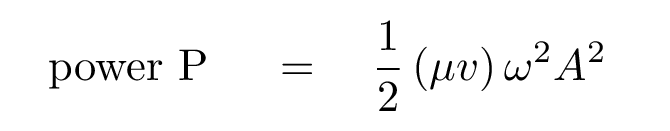
Note that the power depends strongly on both the amplitude of the wave, and on the frequency of the wave.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.