Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
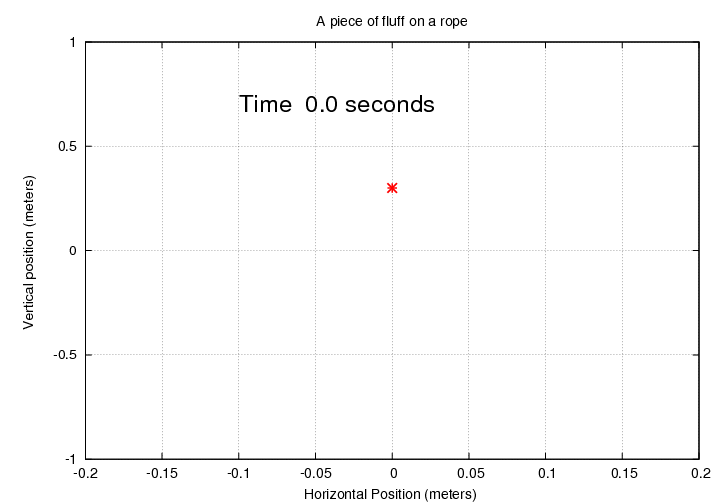
Let's pick a concrete example of simple harmonic motion (SHM). Suppose that you are in the back yard, next to a long, thin rope used to hang laundry; there's nothing hanging from it today. You see a bright red piece of fluff gently float through the air and land on the rope. As you watch, the rope wobbles a bit in the breeze, causing the red fluff to move up and down.
Click on the picture below to start animation.
You check your watch and note that the fluff takes 62.8 seconds to complete 10 full cycles of motion.
Q: Can you write down an equation which describes
the vertical position of the fluff as a function
of time?
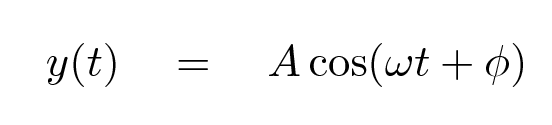
Q: What are the values and units of the quantities
A
ω
φ
That wasn't so hard. We can display this motion graphically by making a plot in which time runs along the horizontal axis and the position of the fluff is shown on the vertical axis, like this:
Click on the picture below to start animation.
Look at the time between two successive peak positions of the fluff.
Q: What is the quantity T shown in this graph? Q: How is it related to the angular frequency ω?
However, we can also, if we wish, pay attention to the OTHER PORTIONS of the rope, the sections on either side of the red piece of fluff. Suppose that we use a camera to take a picture of the rope around the fluff. It might look like this:
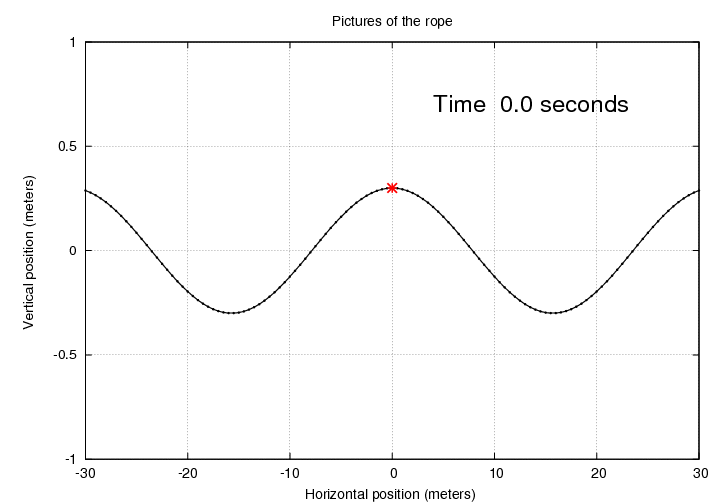
Q: Can you write down an equation which describes
the vertical position of the rope as a function
of POSITION (not time)?
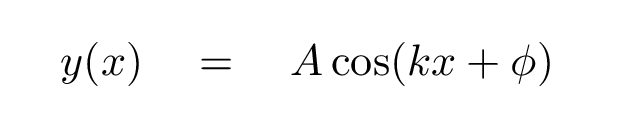
Look at the distance between two successive trough positions of the fluff.
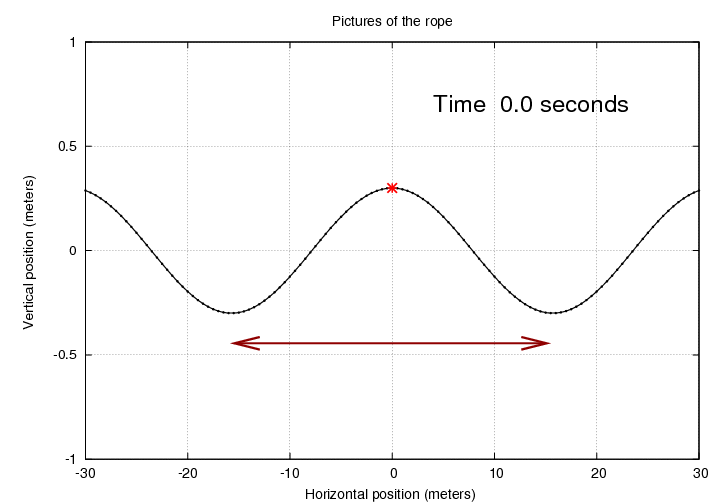
Q: What is the quantity shown in this graph? Q: How is it related to the constant k in the equation above?
Hey, that looks pretty familiar. But this time, the argument of the cosine function isn't an angular frequency -- it's a spatial frequency. The quantity multiplied by the position is called the wave number k.
radians 2 π radians
ω = angular frequency = ------- = ---------
second period T
radians 2 π radians
k = wave number = ------- = ----------
meter wavelength λ
Now, what happens if we watch the rope over a long stretch of space, and over a long stretch of time?
Click on the picture below to start animation.
Q: Does the fluff move horizontally? Q: Does any of the rope move horizontally? Q: Does the pattern of the wave move horizontally?
Yes, in general, the PATTERN of a wave does move through space, even if the individual pieces of rope -- or air, or water -- are simply oscillating back and forth and not translating in any fixed direction over long periods of time.
Not all waves move in this fashion, but many do. Those which do move are called travelling waves,
How fast does the pattern move? It would be nice to express this speed in the standard units of meters per second. How can we do that?
radians
We have ω = -------------
second
radians
k = -------------
meter
How can we combine these quantities to yield
a speed?
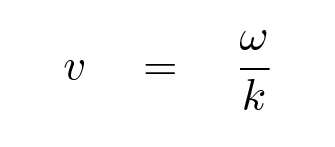
Right. So, putting everything together, we can write the equation for a travelling wave as a combination of an oscillation in time (good old SHM) and also in space:
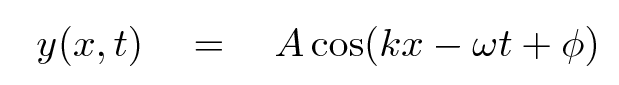
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.