Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
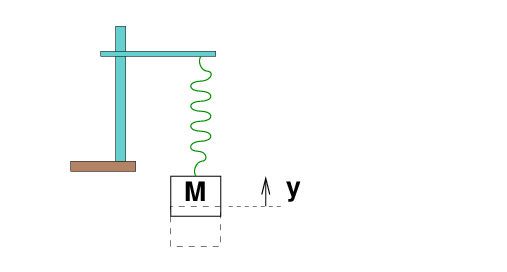
Suppose that a block of mass M = 2 kg hangs from a spring of force constant k = 20 N/m. The block is at rest, motionless.
You then raise the block a distance y = 0.1 m vertically, and release it. The block starts to bob up and down, up and down.
Q: Can you write an equation which describes the
position of the block as a function of time?
Right. It looks like this:
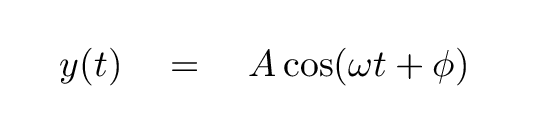
Q: In this particular case, what is the value of the
amplitude A?
Q: In this particular case, what is the value of the
angular frequency ω?
But that only tells us the position of the block. What if we want to know how fast the block is moving at any time -- the velocity of the block? Is there some way to write down the velocity as a simple function of time?
Indeed there is: take the derivative of position with respect to time.
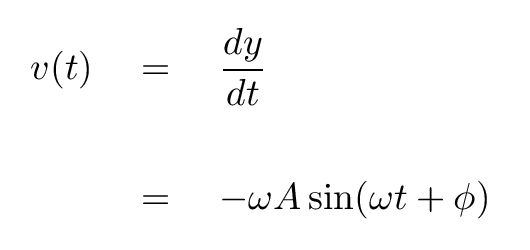
Q: In this particular case, what is the maximum
speed of the block?
In a similar manner, we can compute the acceleration of the block at any time by taking the time derivative of the velocity:
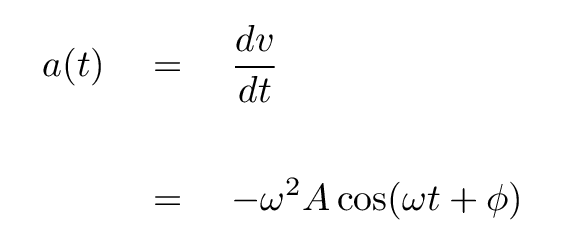
Q: In this particular case, what is the maximum
acceleration of the block?
If we can figure out the velocity of an object moving in SHM, then we can determine its kinetic energy.
Q: What is the connection between kinetic energy and velocity?
Right.
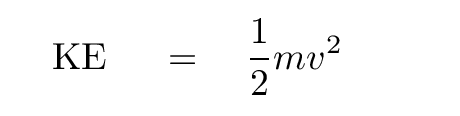
So, using our block and spring as an example, can you write down an equation for kinetic energy as a function of time?
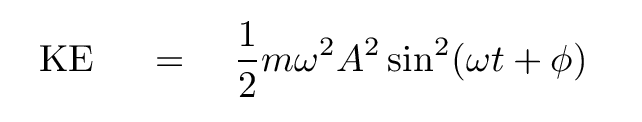
Q: In this particular case, what is the maximum KE
of the block?
Q: In this particular case, what is the minimum KE
of the block?
Suppose that the phase constant φ = 0.
Q: At what time does the KE first reach its maximum value?
Q: Where is the block at that moment?
The potential energy of a block oscillating from a spring consists of contributions from two sources:
If we choose to measure the potential energy as zero when the block is at equilibrium (which means that the spring is NOT at its rest length, but instead stretched out beyond the rest length), then these two contributions can be expressed in a simple, single equation:
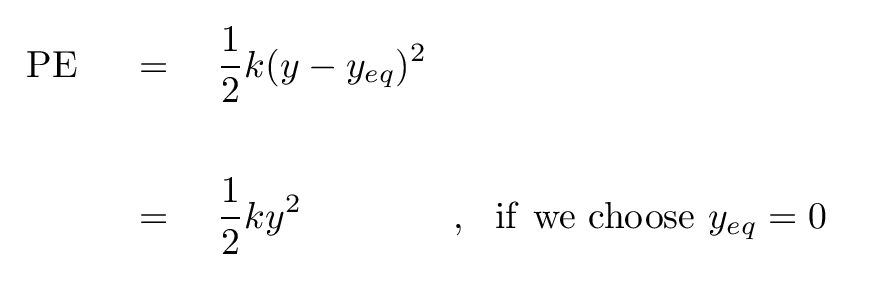
So, using our block and spring as an example, can you write down an equation for potential energy as a function of time?
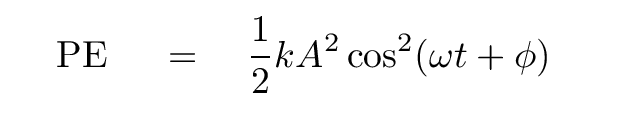
Q: In this particular case, what is the maximum PE
of the block?
Q: In this particular case, what is the minimum PE
of the block?
Suppose that the phase constant φ = 0.
Q: At what time does the PE first reach its maximum value?
Q: Where is the block at that moment?
Do you notice some sort of connection between the kinetic energy and potential energy of the block as it oscillates?
Q: Can you write a single equation for the total energy
KE + PE
of the block as a function of time?
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.