Image courtesy of Wikipedia
There are many situations in which some object finds itself in an equilibrium position, at which it is subject to zero net force; but, if the object moves away from the equilibrium position, it experiences a force pushing/pulling it back.

Image courtesy of
Wikipedia

Image courtesy of
Yutzy's Farm Market

Image courtesy of
My Crazy Life as a Farmer's Wife
One example of this situation involves a mass attached to a spring.
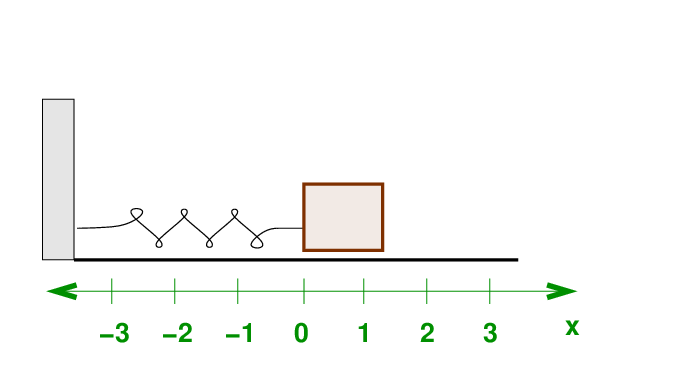
Q: What happens if we move the block to x = 1 ? Q: What happens if we move the block to x = 2 ?
Right. The spring will pull the block back to the left, in the negative-x direction. If we displace the block by twice as much, the spring pulls back twice as hard.
Q: What happens if we move the block to x = -1 ?
Right again. This time, the spring will push back, exerting a force in the positive-x direction.
If we move the block to many different positions and measure the force exerted by the spring each time, we'll find a simple relationship:
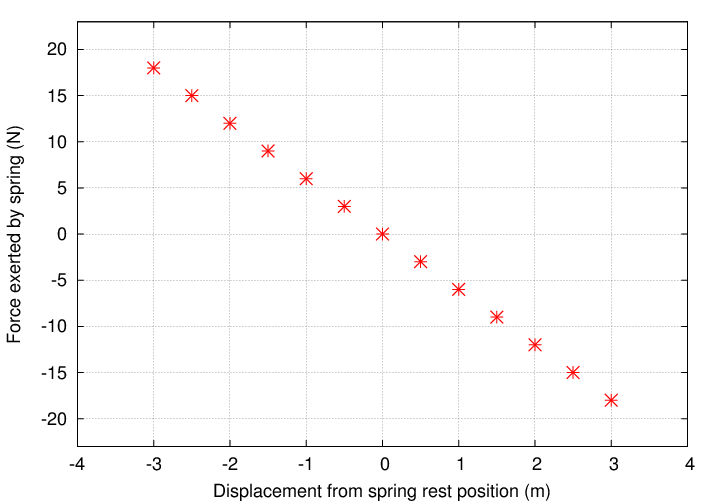
We can write this relationship as an equation; you may have seen this before. It is sometimes called Hooke's Law.
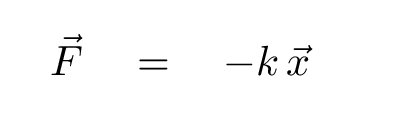
The k in the equation is called the spring constant; it depends on the physical nature of the spring. Stiff springs have a large value of k, and loose springs have a small value.
Q: What are the units of the spring constant?
Okey-dokey. Let's take this relationship to a higher mathematical level, writing it as a differential equation. We begin by using Newton's First Law to replace "force" by a combination of "mass" and "acceleration".
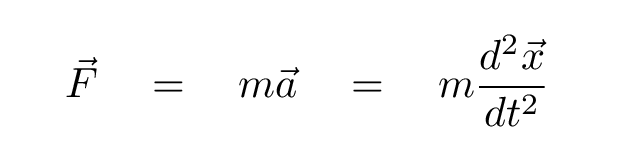
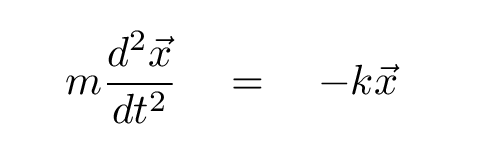
Now, I'll re-arrange things so that the left-hand side consists solely of a second derivative. The result should look familiar to you.
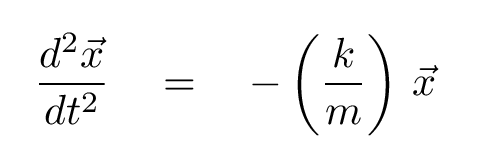
Q: What is the function x(t) that solves
this differential equation?
Yes -- you can write the solution two ways:
We're going to stick with the first option in this class, so one general solution to the motion of a mass attached to a spring is
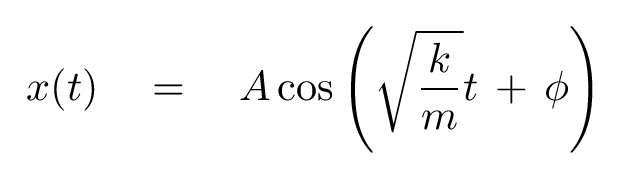
That combination of the spring constant k and the mass of the block m occurs over and over again, and repeatedly writing it inside a square-root sign is awkward; so, physicists have come up with a shortcut: they define the angular frequency of an oscillating system to be
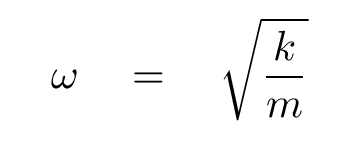
With this substitution, the equation of motion for a mass attached to a spring becomes
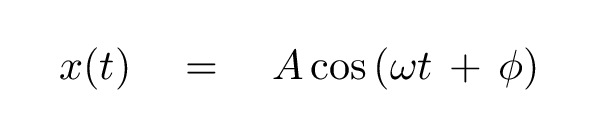
Let me stop here for a moment to summarize the important point: if an object is subject to a linear restoring force,
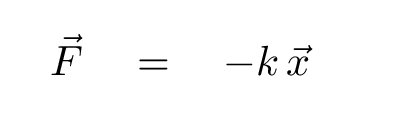
then its equation of motion can be expressed as a second-order differential equation
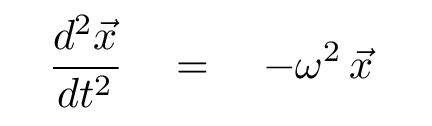
Any such object will undergo Simple Harmonic Motion (SHM) if displaced from its equilibrium. In other words, it will oscillate around the equilibrium point in a sinusoidal manner as a function of time.
Which brings us back to this equation:
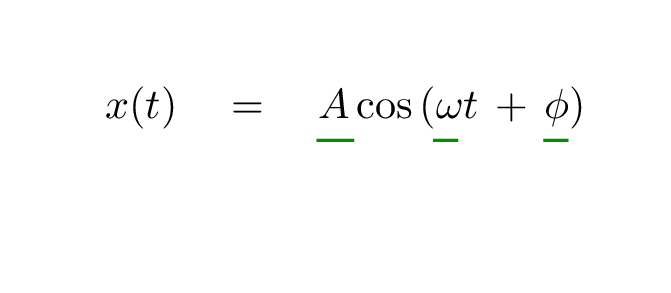
Q: What are the meanings of the underlined values?
What are their units?
Let's take a look at a graph of this function to illustrate the answers.
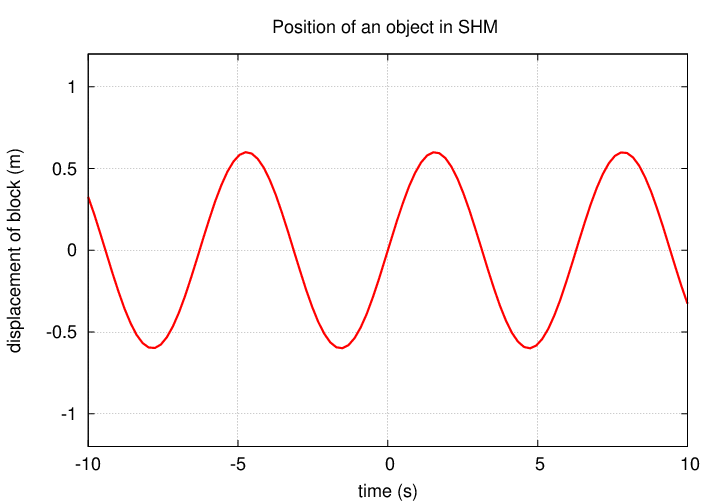
The amplitude A controls the limits of the oscillation.
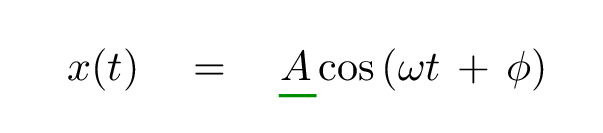
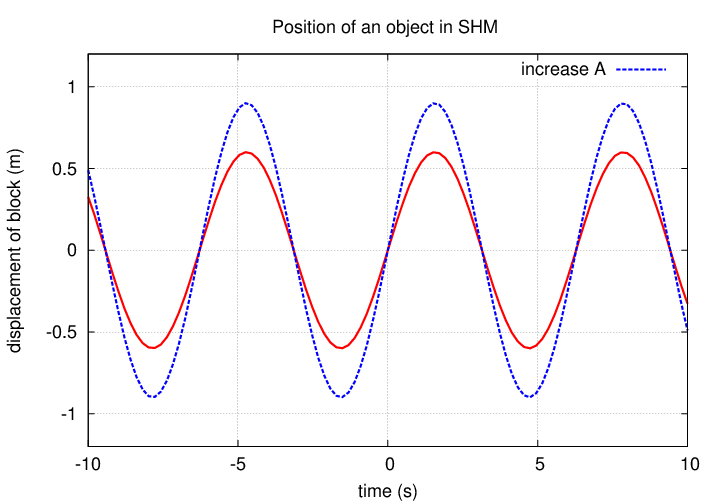
The angular frequency ω controls how quickly the oscillation occurs.
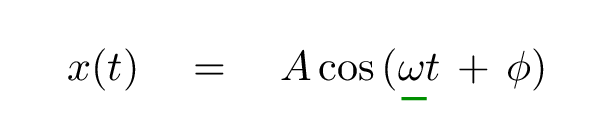
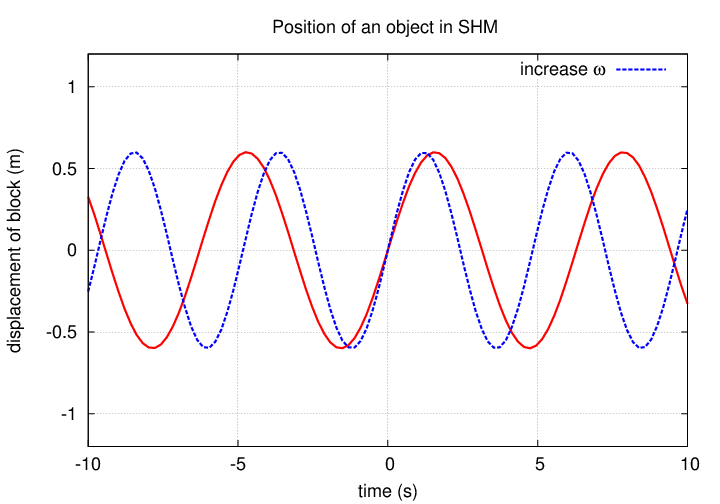
The phase shift φ controls the starting time of the oscillation.
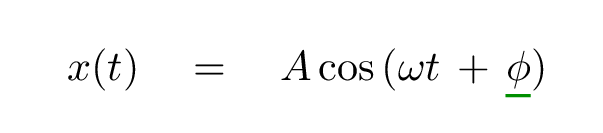
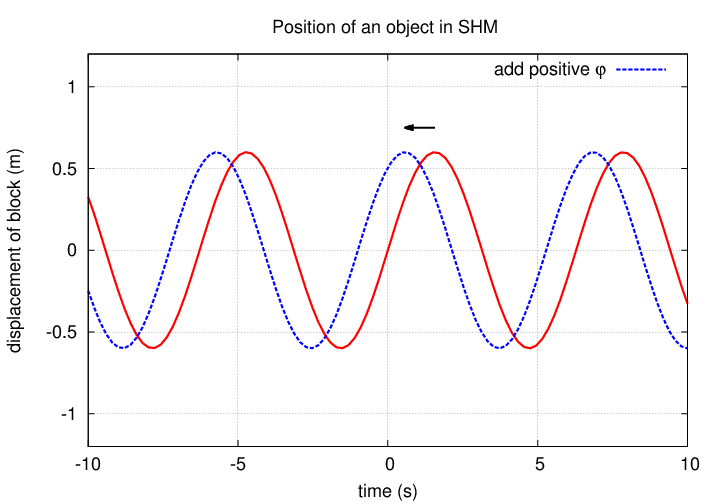
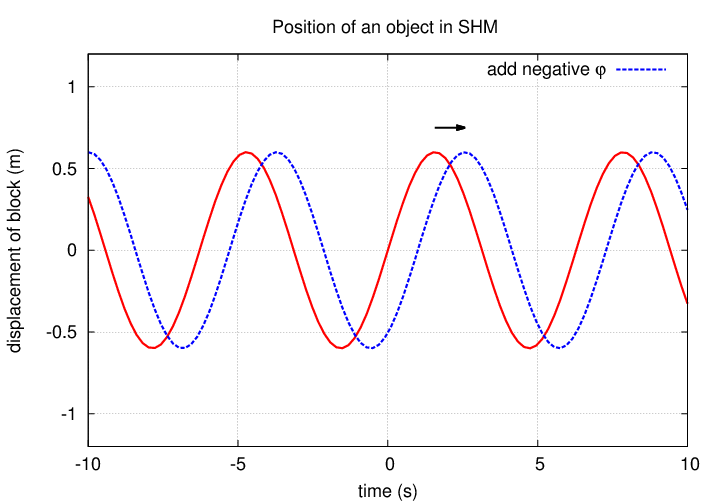
In summary, for our example of the block attached to a spring,
variable symbol units
-------------------------------------------------------
amplitude A meters
2 π
angular frequency ω rad/sec = -------
Period
phase shift φ rad
-------------------------------------------------------