 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.

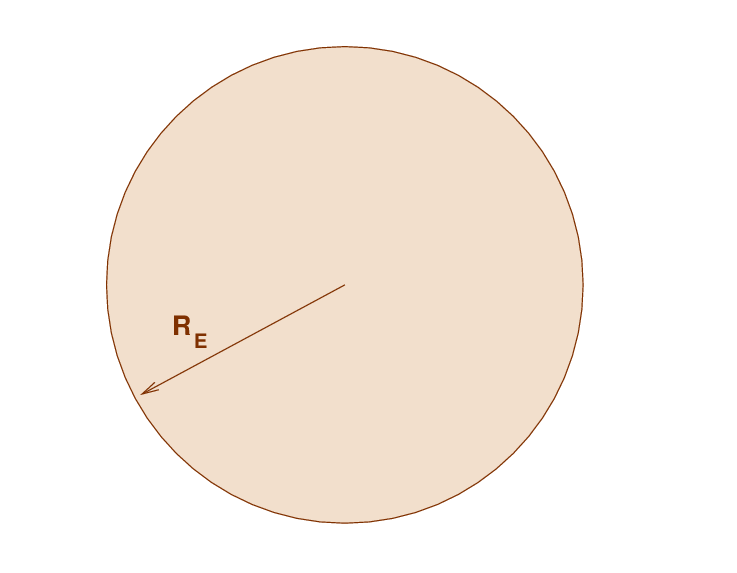
Consider the (simplified) Earth: a sphere of radius RE and constant density ρ.
Q: What is the mass of the Earth?
Q: Joe stands on the surface of the Earth. He drops a ball.
How fast does the ball accelerate as it falls?
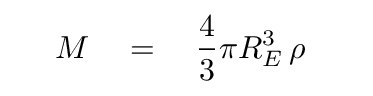
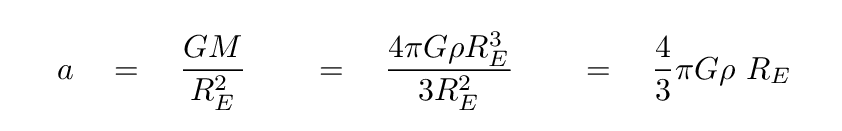
Q: What is the numerical value of this acceleration in
meters per second-squared?
Good. Now, Joe hears that there's a pirate treasure buried far below the surface, so he starts to dig a tunnel. He goes down pretty far, to a point at which the distance from the center of the Earth to the bottom of the tunnel is x.
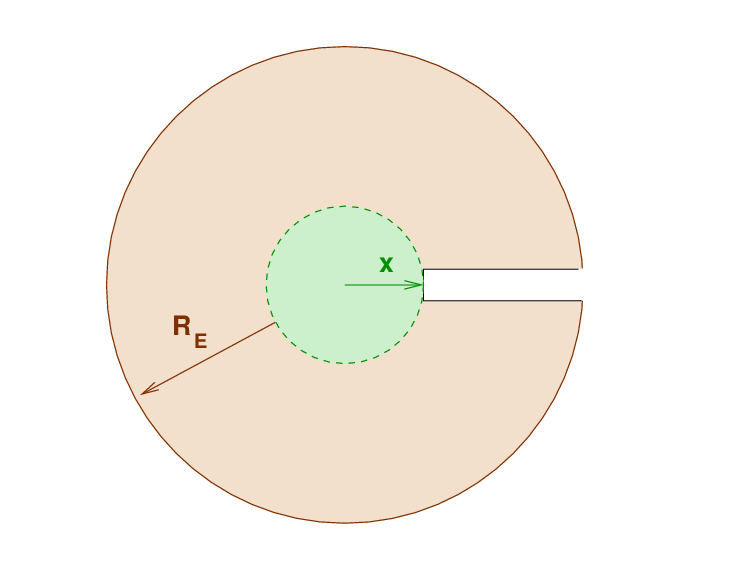
Joe stops here to take a break. He pulls a ball out of his pocket and drops it. The ball does accelerate downward .... but not at the same old rate.
Why not? It turns out that the gravitational force on an object embedded in a spherical distribution of matter depends only on the mass which is closer to the interior. In other words, the gravitational force on the ball depends only on the mass within the green area, which is at a radius less than or equal to x.
Q: What is the mass interior to Joe's position x? Q: How fast does the ball accelerate as it falls?
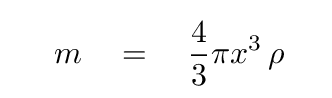
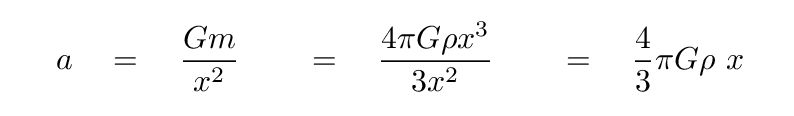
Now, if we express Joe's displacement from the center of the Earth as a vector, then his current position is in the POSITIVE x-direction; but the acceleration of the ball is opposite to that:
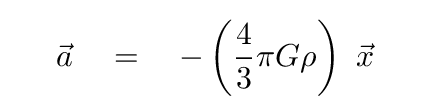
Or, if we write the acceleration in terms of the time derivative of position,
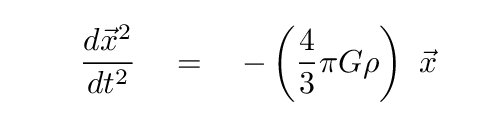
Q: Does this acceleration change with location?
Q: If Joe managed to dig to the center of the Earth,
what would the acceleration be there?
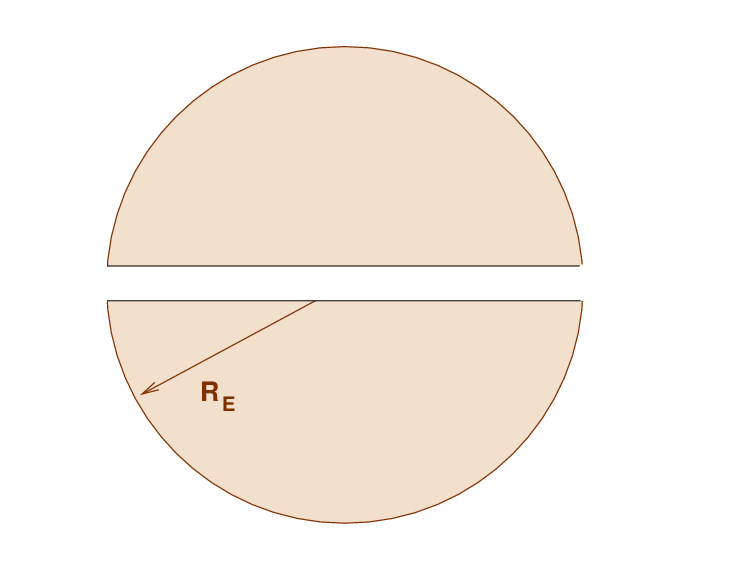
Joe is finished with his lunch break. He continues to dig, going straight through the center of the Earth and out towards the surface again.
As he stands on the surface again, next to his tunnel, Joe holds the ball in his hand. He then drops it into the tunnel.
Q: What happens to the ball?
Q: Does it undergo simple harmonic motion?
Q: Can you write an equation for the position
of the ball as a function of time?
x(t) = ....
Well, if you use that big coefficient on the right-hand side of the differential equation to define an angular frequency ω,
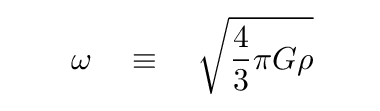
then you can write an equation of motion very simply.
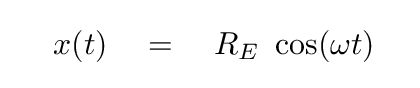
Q: How long will it take for the ball to fall all
the way through the tunnel, reach the other side
of the Earth, and then return to Joe?
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.