
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
You've seen one kind of oscillatory motion -- a mass on a spring moving up and down, up and down -- which can be described by SHM. But the beauty of SHM, and the reason why we are spending several weeks studying it, is that it can be used to analyze many different situations.
For example, consider an object swinging back and forth, back and forth. It certainly isn't the same thing as a mass on a spring ...

... but we can still describe its motion using the same mathematical language of simple harmonic motion.
We're going to analyze this pendulum using angular quantities. It's possible to use linear quantities, too, and you'll end up with the same result.
Suppose that a pendulum with length L and mass M is displaced by an angular distance θ radians away from its rest position.
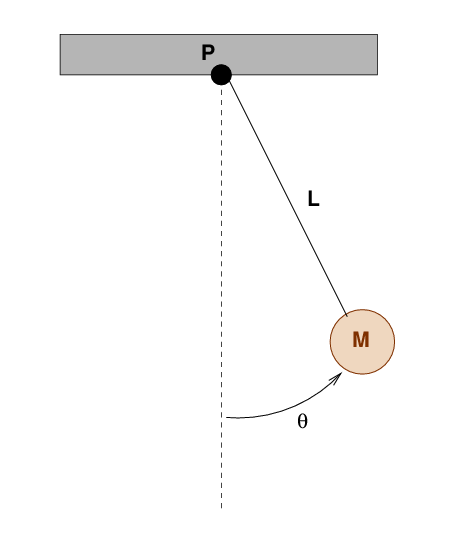
Q: Which direction is the angular displacement θ?
There are two forces acting on the pendulum bob: tension T and gravity Fg.
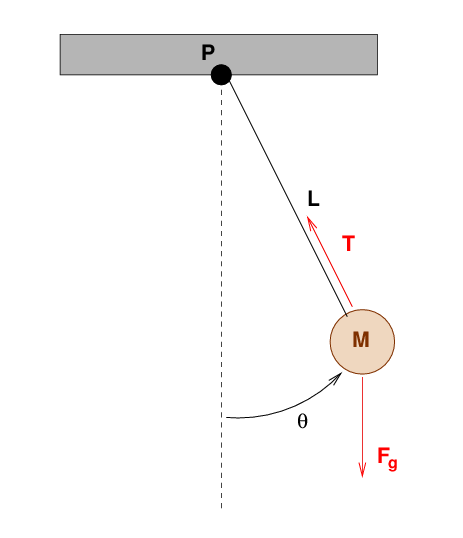
Can you compute the torque due to each of these forces around the pendulum's attachment to the ceiling, at point P?
Right. The torque around P due to the tension in the string, T, is zero, because the force is applied at the point P itself.
But the torque around P due to the force of gravity is not zero. Instead, we compute it like so:
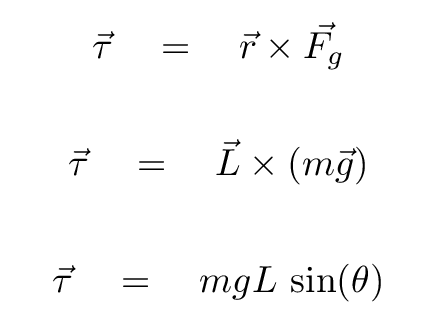
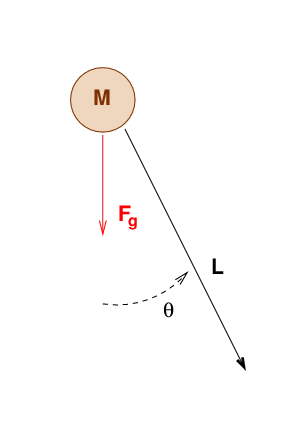
Q: Which direction is the torque τ?
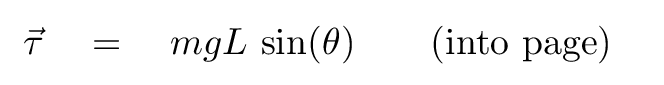
Okay, that's the torque on the pendulum bob. In order to figure out how it reacts to this torque, we need to compute its moment of inertia.
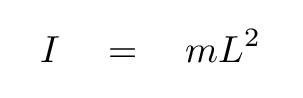
Newton's Second Law, in the linear realm, is good old F = ma. When we deal with angular quantities, it looks a little different:
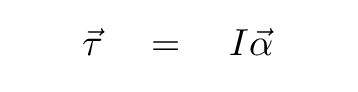
So, if we re-arrange this to put the torque (which we know) and the moment of inertia (which we know) on the right-hand side, we end up with an expression for the angular acceleration α of the pendulum bob.
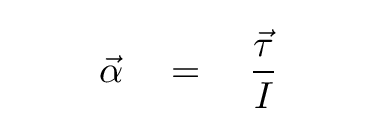
Q: What happens when we insert our values for the
torque on the bob, and its moment of inertia?
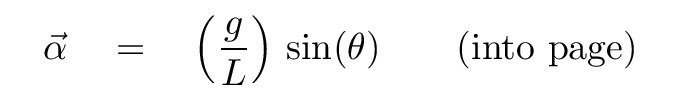
Now, at this point, we can simplify things by allowing the pendulum to swing only through a relatively small angle; say, no more than 10 degrees or so.
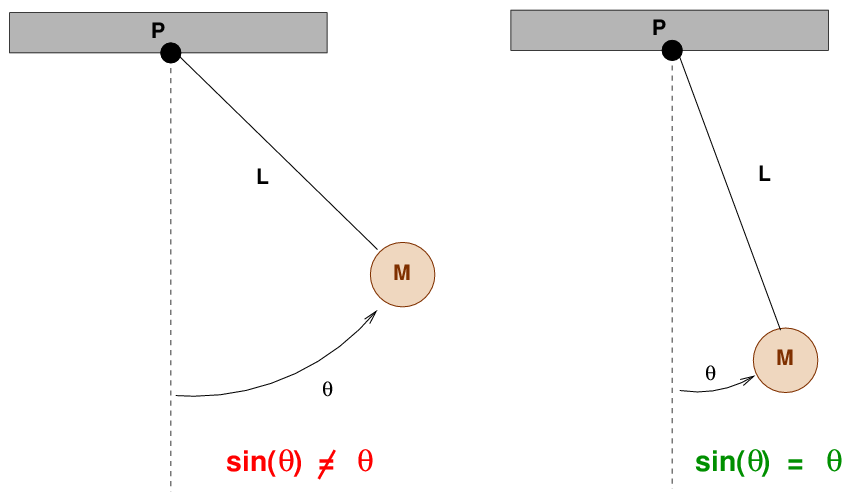
If the angular displacement is always small, then we can take advantage of a very nice coincidence called the small angle approximation: the sine of a small angle is approximately equal to the angle itself, expressed in radians.
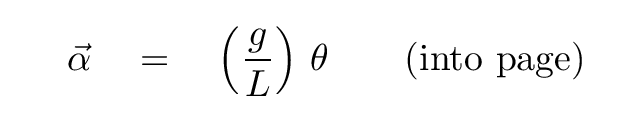
Now, can you remember something about the angular displacement θ itself that you answered way back at the start of today's discussion?
Q: Which direction is the angular displacement θ?
Right. The direction of the displacement θ is OUT of the page, which means that the vector θ points OUT of the page. So, if we want to write the angular acceleration in terms of this vector θ, we have to insert a negative sign:
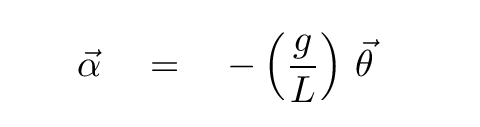
Well, all this is fine, but how is it connected to simple harmonic motion, or the box attached to a spring?
The key is to realize that angular acceleration α is the second derivative with respect to time of the angular displacement θ. When we write things that way, we end up with a differential equation that should look very familiar to you.
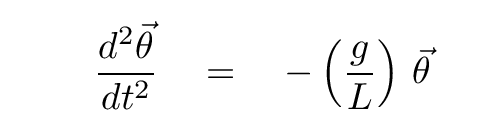
Look familiar?
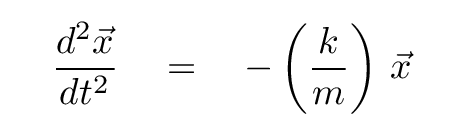
Just as the solution to the linear version was a sine or cosine function, the solution to the angular motion of a pendulum is a sine or cosine function of time.
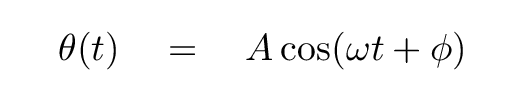
And, just as the angular frequency of the mass attached to a spring depended on the square root of some quantities, the angular frequency of a pendulum will also depend on the square root of some quantities.
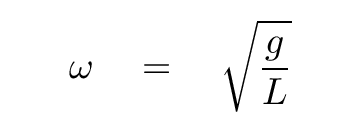
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.