Simple Harmonic Motion in Action

You've been learning about the theory behind simple harmonic motion (SHM) .... so let's put it into practice.

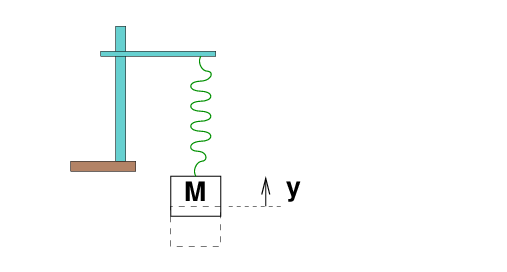
Set up equipment at your table so that you can hang a m = 50 g mass from a silver harmonic spring (one of the silver mass hangers is a good choice for the mass). We will treat this mass as perfect; let's assume that it has no uncertainty at all.

Allow the mass to come to rest as it hangs from the spring. Then, displace it slightly upwards and release it. The mass will bob up and down, up and down.

Measure the time it takes for the mass to complete N = 20 oscillations.
Make 3 trials, and record the times for each trial.
Calculate the period P for each trial.
Compute the average period.
Compute the standard deviation of the periods; use this as the uncertainty
What is the percentage uncertainty in the period?

So far, so good. Let's now connect this experiment to the theory of simple harmonic motion. In theory, the angular frequency ω of an item attached to a spring is related to the mass m of the object, and the spring constant k, like so:

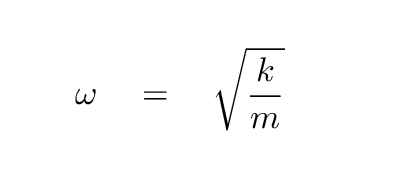
(If you are wondering how to derive this for a mass hanging from a spring, you might look at the situation in a bit more detail. )

Use your measurement of the period to determine the angular frequency ω. What are the units?
What is the uncertainty in the angular frequency?
What is the percentage uncertainty in the angular frequency?
Compute the spring constant k of your spring. What are the units?
What is the uncertainty in the spring constant?
What is the percentage uncertainty in the spring constant?

Do as much of these calculations as you can during the class period. If necessary, you may continue to work on them after class, and bring your results to the next class meeting.

Bonus! You computed the percentage uncertainty of three quantities: the period of the oscillation, the angular frequency of the oscillation, and the spring constant. Were all three percentages the same? If not, can you explain why?