Adding waves (of the same frequency) together

So, the general rule is, 



   When two waves meet .... just ADD their wave functions together

The problem is that, in general, adding together two functions which look like this:

is not really easy. In fact, it's a pain in the neck.

However, there are some relatively common situations in which this combination of waves is not so difficult. Let's make a little list of the various situations, from most simple to least simple:

  1. same frequency, same amplitude -- REALLY easy (today)
  2. same frequency, different amplitude -- sort of easy (phasors, two weeks from now)
  3. slightly different frequency -- hard (beats, two weeks)
  4. different frequency, different amplitude -- REALLY hard (never)

Easy: adding two waves which have the same frequency and amplitude ....

Suppose that two waves meet. They have the same frequency, and the same amplitude (and the same wave number .... but that's often tied together with the frequency).

So, the only difference between the two is a phase offset.

To add these two wave functions together, we can use a good ol' trigonometric formula; maybe you remember it from your deep, dark past. 



  Q:  Please use this trig identity to add together the
          two sine waves y1(x,t) and y2(x,t).

What do you get?

But what does it mean? 

 


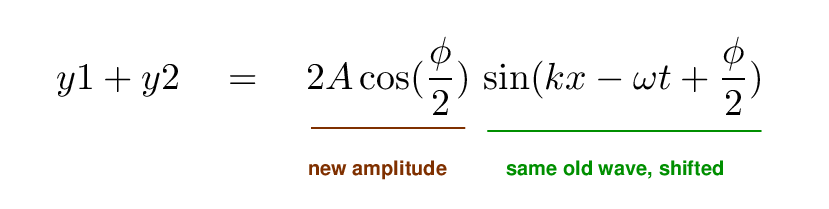
    Q:  Two travelling waves meet:

          y1  =  (5 cm) * sin ( 3 rad/m * x  -  0.1 rad/s * t )

          y2  =  (5 cm) * sin ( 3 rad/m * x  -  0.1 rad/s * t  +  1 rad )


        Is the amplitude of the combined wave 

              a)  bigger than either original wave

              b)  smaller than either original wave

              c)  the same as either original wave


        What is the SPEED of this combined wave?