Adding waves of DIFFERENT frequencies together

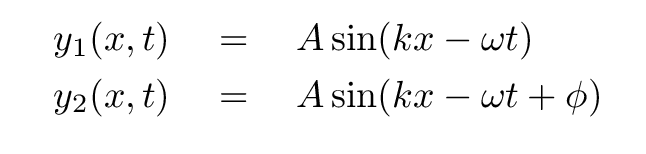
You ought to remember what to do when two waves meet, if the two waves have the same frequency, same amplitude, and differ only by a phase offset.

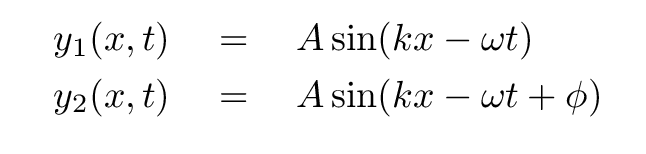
  Q:  What is a quick and easy way to add these waves?

Right -- use a good old-fashioned trigonometric formula:

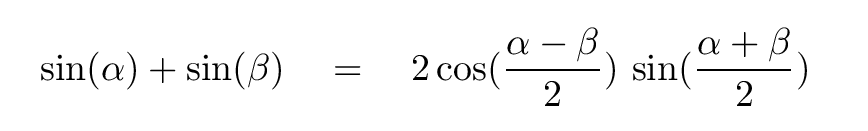
But what if the two waves don't have the same frequency?

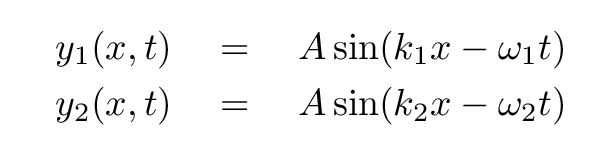
  Q:  Can we still use the same trig identity?

Yes! Yes, we can. Go ahead and use that trig identity. What is the result of adding the two waves?

If we define these terms (which simplify the final answer),

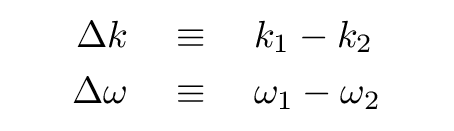
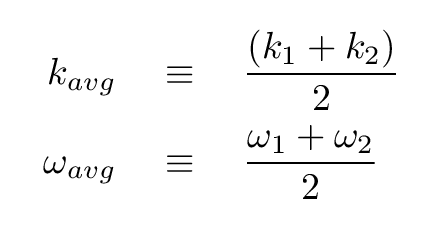
then the sum of the two waves is

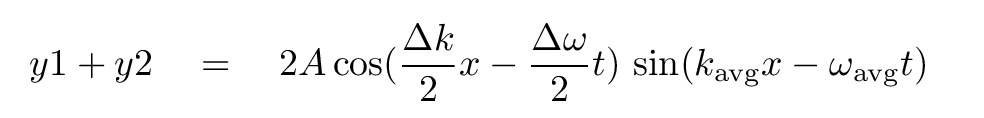
But what does it mean?

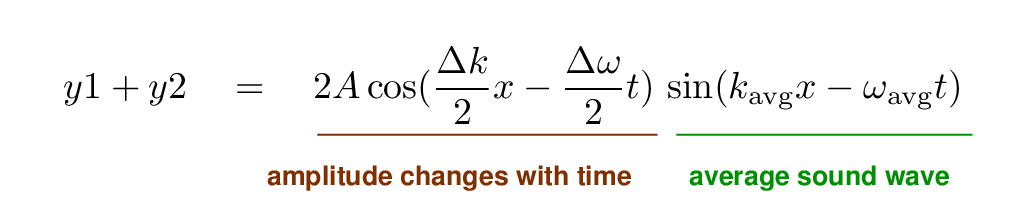
Let's look at the waves which result from this combination. If we pick a relatively short period of time, then the sum appears to be similar to either of the input waves: a simple sinusoid.

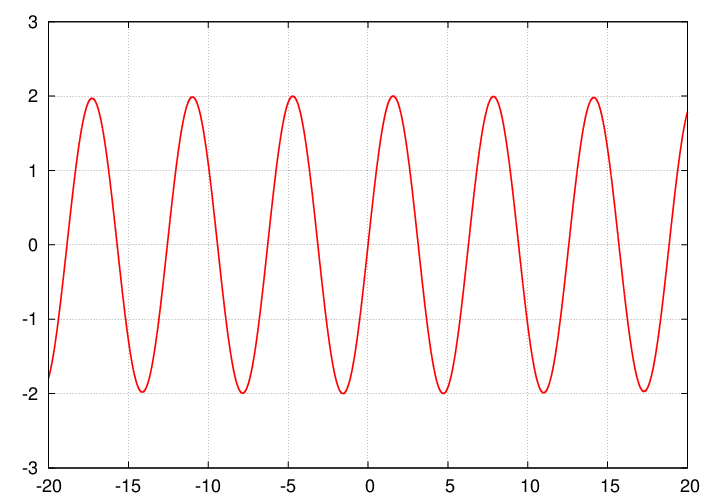
But if we look at a longer duration, we see that the amplitude of the combined wave is changing with time:

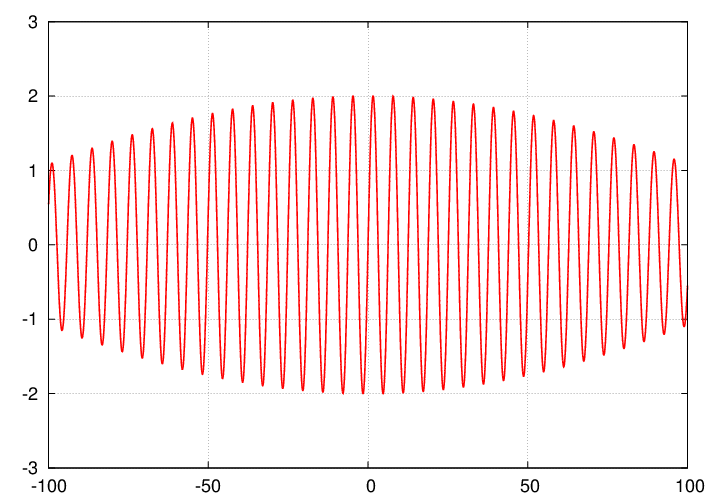
In fact, the amplitude drops to zero at certain times, then recovers and reaches a maximum amplitude, then falls to zero again.

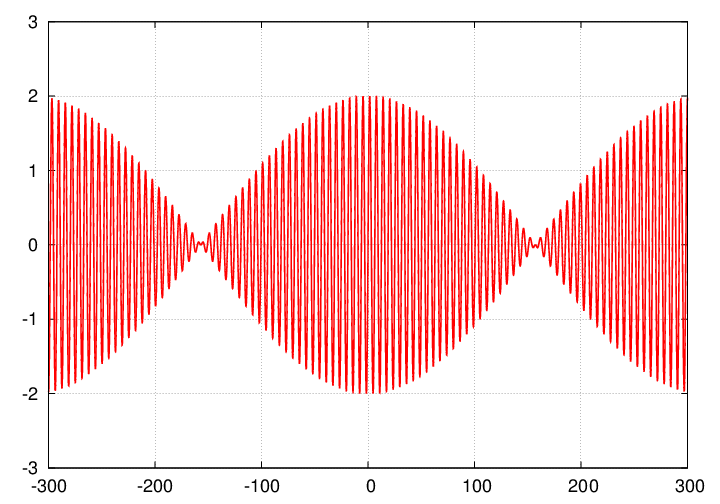
The resulting combination has what are called beats: repeated variations in amplitude at a frequency related to the difference in original wave frequencies.

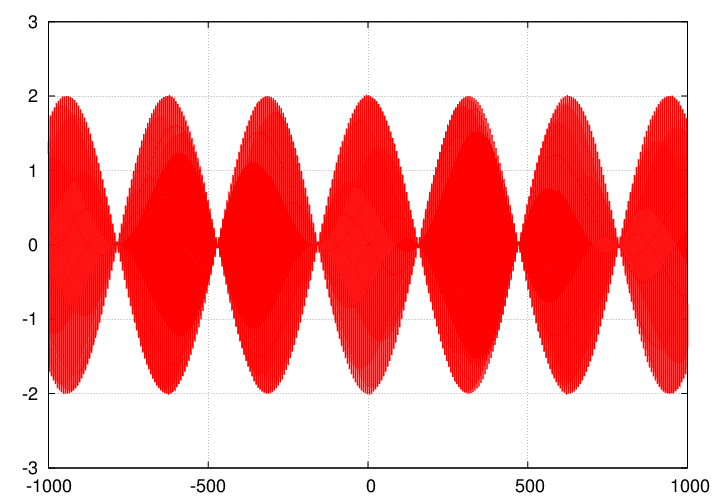
In the case of sound waves produced by two sources with slightly different frequencies, we hear something like

     .....wwwwaaaAAAAAAAAaaaawwww....  .....wwwwaaaAAAAAAAAaaaawwww....  .....wwwwaaaAAAAAAAAaaaawwww.... 

  Q:  Two guitar strings are plucked, producing sound waves
      with frequencies

              f1  =   256  Hz

              f2  =   258  Hz

      How many "waah waah waahs" do you hear each second?