Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
The neutrino is an elusive sub-atomic particle: it hardly ever interacts with matter, which makes it very difficult to detect and study. For many years after its discovery, it was thought to have no rest mass at all, like the photon. In recent years, physicists have determined that it does have mass, but only a small amount -- much much less than electrons.
Back in 1987, when the mass of the neutrino was still an open question, astronomers saw a star explode in a nearby galaxy. That explosion, plus a little bit of special relativity, allowed scientists to place strong limits on the mass of the neutrino; not really pin it down, but at least rule out some possibilities.
Recall from last time that if two particles are produced at the same time, and travel towards the same distant location,
On February 23, 1987, a massive star in one of the Milky Way's nearest neighboring galaxies, the Large Magellanic Cloud (LMC for short), suddenly became thousands of times brighter than it had ever been before.
Image credit and copyright:
AURA
NOAO
NSF
It was a supernova: the violent explosion of a massive star when it runs out of fuel in its core.
Theoretical models of supernovae predict that they should produce lots of neutrinos, as protons and electrons are crushed together in the collapse of the stellar core:
Particle physicists who happened to be running experiments at two neutrino detectors -- at Brookhaven in the US and Kamiokande in Japan -- quickly looked at their records. It turned out that each group had detected a small burst of neutrinos early on the morning of February 23.
The Japanese group counted 11 or 12 (it depends on which paper one reads) neutrinos which came from the direction of the LMC.
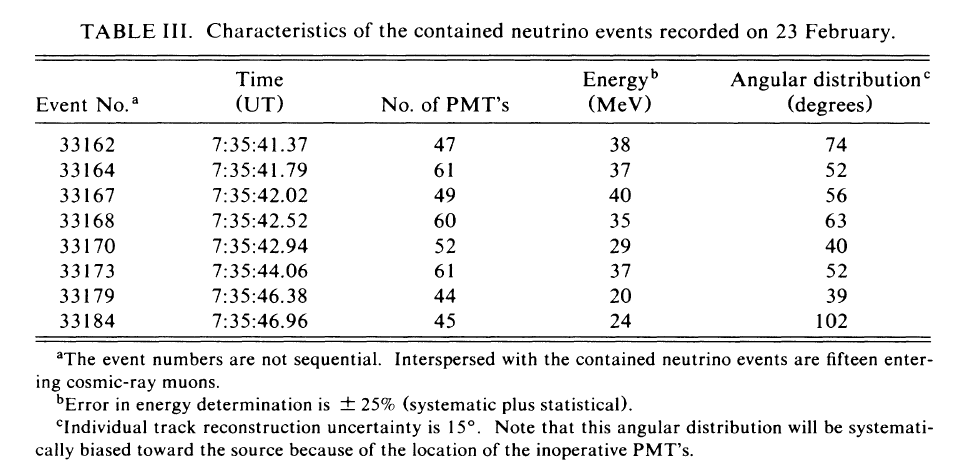
The Brookhaven group counted 8 neutrinos which came from the direction of the LMC:
Q: Did the high-energy neutrinos arrive earlier
than the low-energy neutrinos?
When I look at the Brookhaven numbers, I can derive some quick-and-dirty estimates. It appears to me that
so let's use these numbers.
(Since these aren't exactly the same as the values adopted by the scientists who analyzed these results very carefully, our results won't match their exactly. However, we can expect to derive a limit which is consistent with theirs to within an order of magntiude )
Astronomers have measured the distance to the LMC reasonably well. It is about D = 50 kiloparsecs away from the Earth.
Q: If 1 pc = 3.1 x 10^(16) m,
how long should it take light to
fly from the supernova to the Earth?
Call this time t0
The answer
Suppose that we GUESS that the collapse of the core inside the star was such a sudden event that it created a burst of neutrinos all at once. Then the difference of just 5 seconds in arrival time, after travelling through space for over 150,000 years, must be due to the very slightly higher speed of the high-energy neutrinos. Using this information, plus the connection between energy and rest mass of a particle, we can estimate what the mass of the neutrino; or, more accurately, we can place an upper limit on its mass. After all, it is also possible that the collapse of the star's core took a few seconds, so that some neutrinos were really created a few seconds earlier, and so they got a few seconds' head start towards the Earth.
So, let's begin the process of estimating an upper limit to the mass of the neutrino. The first step is to use the energies of the earliest and latest neutrinos to find some ratio of their gamma factors.
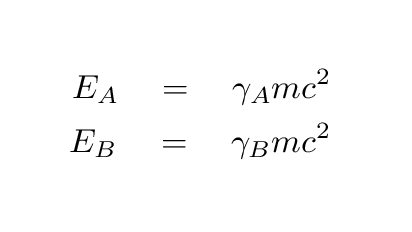
What is the ratio of the gamma factors? Specifically, can you compute the ratio
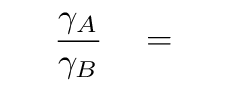
and then use it to compute the value of the low-energy particle's gamma factor in terms of high-energy particle's gamma factor?
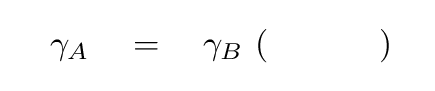
Okay, write that down somewhere safe, and let's move on to the second step. We need to write down an expression for the time it takes the high-energy neutrino A to travel the distance D from the supernova to the Earth.
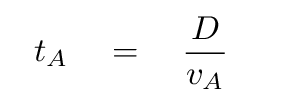
We can use the connection between the velocity of a particle and its gamma factor
to write the travel time like this:
Your turn now:
Q: Use the binomial expansion to write the
time for neutrino A to reach the
Earth in a form that looks like
t0 + t0 * ( something )
Right. The result is
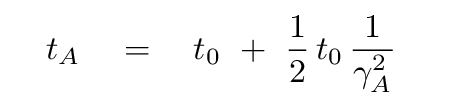
We can in exactly the same way figure out that the time it takes for neutrino B, the low-energy neutrino, to reach the Earth must be
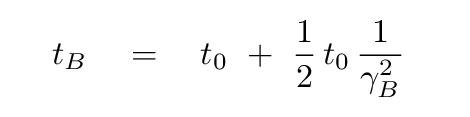
Okay, your turn again. What is the difference between the arrival times of the two neutrinos? Try to come up with an expression like this:
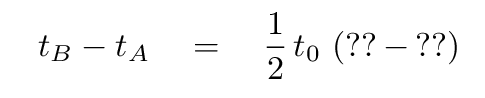
Right again.
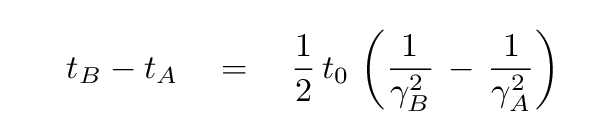
Okay. Now, look back at the relationship you derived earlier between the gamma factors for these two particles. Use that expression to get rid of the gamma(A) in the time difference, so that the right-hand side is written entirely as a function of the gamma(B) factor.
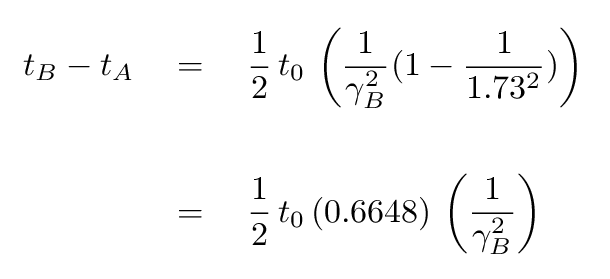
Great! Since you know the difference in arrival times t(B) - t(A), and you know the light-travel time from the supernova to the Earth t0, you can compute the gamma factor of the low-energy neutrino B.
Q: What is the gamma factor for neutrino B?The answer.
Okay! Recall that the low-energy neutrinos which arrived last had an energy of around 22 MeV = 3.5 x 10^(-12) Joules. If we assume that all the neutrinos were created at exactly the same moment, so that the entire difference in arrival times t(B) - t(A) must be due to the difference in their speeds, then we can estimate the mass of the neutrino.
Q: What is this upper limit to the mass of the
neutrino? Express in three ways:
in units of kg
in units of eV/c^2 (1 eV = 1.6 x 10^(-19) Joules)
relative to the electron's mass
The answers.
Let's compare your result to that of some real physicists.
High-energy physicists have continued to investigate the mass of the neutrino. It appears at the current time (2008) that the three flavors of neutrino, electron, muon and tau, are linked so that a single particle can switch from one type to the other under certain circumstances. There are still only upper limits on the mass of each flavor. The current upper limit on the mass of the electron neutrino (the type produced by supernovae like SN 1987A) is about 2 electron-volts, or 4 x 10^(-36) kg, nearly one million times smaller than the mass of the electron.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.