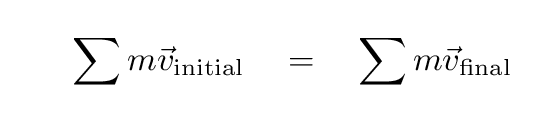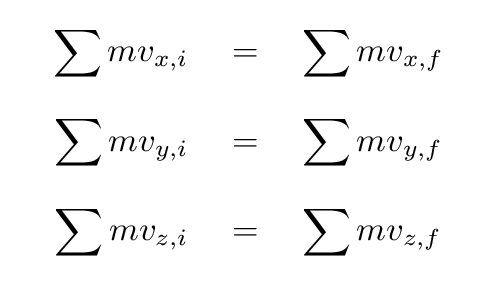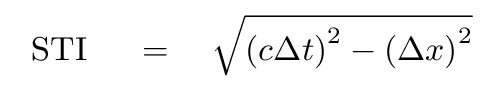Momentum in the low-speed regime

You have probably discussed momentum in an earlier physics course. Momentum is a combination of the mass of a body and its velocity, just like kinetic energy. There are two main differences between KE and momentum, however.

1. Momentum is a vector quantity, whereas KE is a scalar. The momentum of a body has a direction as well as a size; the direction is just the direction of motion.
   

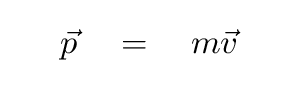
   That means that there are really three quantities involved in the calculation of momentum, not just one.

   
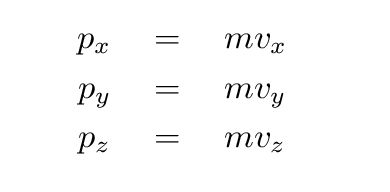
2. The units are different: momentum involves the velocity of the object raised to the first power, whereas KE involves the square of the velocity. That means that the standard SI units for momentum must not be Joules. In fact, the units for momentum don't have a fancy name ....
   

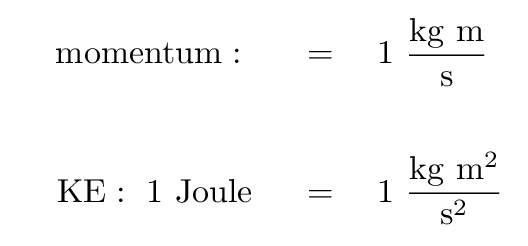
   If, for some reason, we wanted to convert a momentum-like quantity into an energy-like quantity, we would have to multiply by a velocity-like quantity:

   

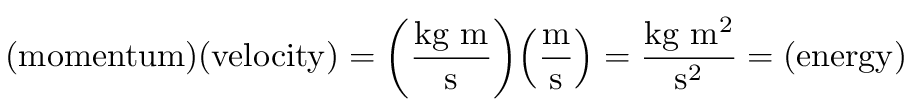
Let's do a few simple examples.

  Q:  I toss a rubber ball of mass m = 0.2 kg
      gently to the East at v = 5 m/s.
 
      What is the ball's momentum?





  Q:  Crazy Ellie fires a 125-grain cartridge from  
      her Smith and Wesson .357 Magnum handgun
      (one grain is approx 0.065 grams).
      The bullet leaves the muzzle of the 
      gun at v = 440 m/s towards the East.

      What is the bullet's momentum?

What good is momentum?

Why bother with momentum? One of the main reasons is that when objects collide or interact, then -- as long as there are no significant external forces -- the initial momentum of the system is the same as the final momentum.

Be careful: this applies to the sum over all the objects involved, not each object individually. In other words,

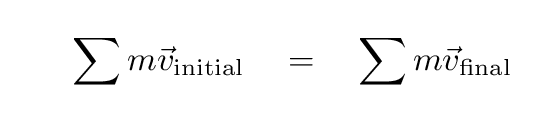
In fact, this equality must apply to each component of the vector momentum, so we could also write an equation for each component separately. I'll use subscripts i to mean "initial" and f to mean "final".

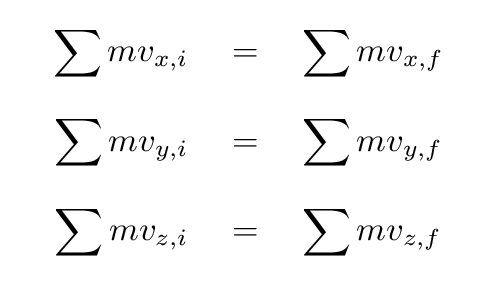
You may recall that when I discussed kinetic energy, I was careful to add lots of qualifiers to the statement "kinetic energy is SOMETIMES conserved in interactions between particles." It was only collisions between hard, compact balls -- the "elastic" collisions -- in which KE was conserved. For example, in this collision between two cars (click on the first picture for a very large movie), KE is definitely NOT conserved:

• both cars are motionless afterwards, so the final KE is zero
• a great deal of KE was dissipated in the process of deforming pieces of metal, breaking glass, and so forth

On the other hand, the total momentum of this pair of cars IS conserved:

• the initial momentum was zero in each direction -- why?
• the final momentum is zero in each direction

Let's work through a few simple examples of momentum in the non-relativistic regime, just to see how it can be used in practice.

Car slams into truck and sticks to it

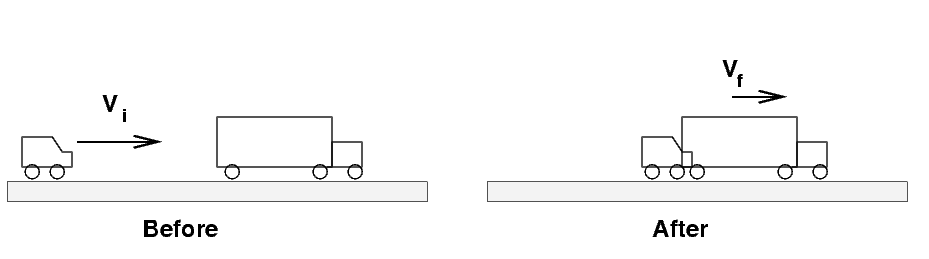
A car of mass m₁ = 2000 kg moving at v_i = 20 m/s slams into a stationary truck of mass m₂ = 15,000 kg. Immediately after they collide, what is the speed with which the combined wreckage slides forward?

Which of the following is the final velocity v_f?

1. 20.0 m/s to the right
2. 4.21 m/s to the right
3. 2.67 m/s to the right
4. 2.35 m/s to the right

Car rolls into truck and bounces off gently

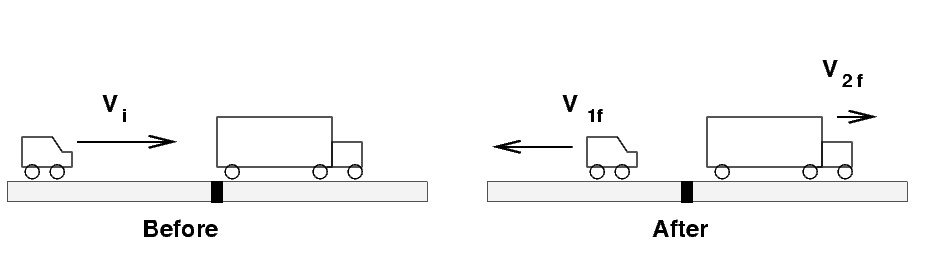
A car of mass m₁ = 2000 kg rolling slowly at v_i = 5 m/s bumps into a stationary truck of mass m₂ = 15,000 kg. Afterwards, the car moves backwards with velocity v_1f, and the truck creeps forward at v_2f.

Which of the following are the final velocities?

1. car 5.0 m/s to the left, truck 1.53 m/s to the right
2. car 2.0 m/s to the left, truck 0.93 m/s to the right
3. car 1.0 m/s to the left, truck 0.53 m/s to the right

Car and minivan smash into each other

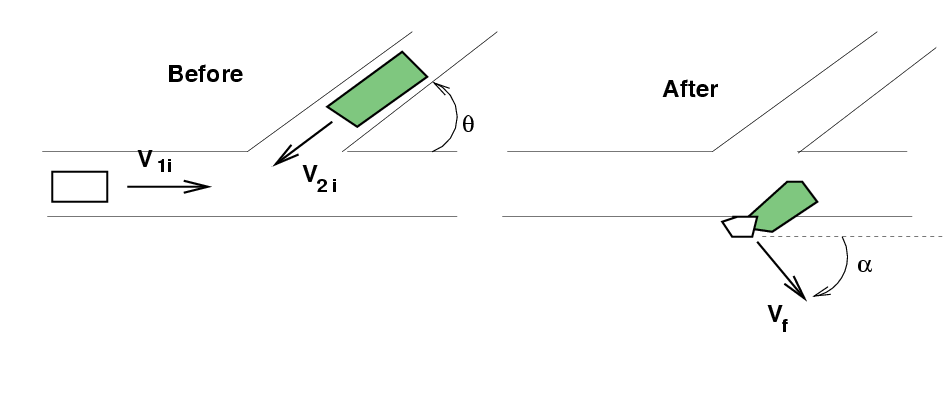
A car of mass m₁ = 2000 kg is driving at v_1i = 20 m/s due East as it enters an intersection. A minivan of mass m₂ = 6000 kg going v_2i = 30 m/s drives into the intersection along a road which runs θ = 30 degrees South of West. The meet in a most unhappy fashion.

Which of the following is the final velocity of the combined wreckage?

1. (-19.3 m/s East, -12.5 m/s North)
2. (-14.5 m/s East, -11.3 m/s North)
3. (-11.3 m/s East, -15.3 m/s North)

If the angle α is drawn as shown, how large is it?

1. about 38 degrees
2. about 128 degrees
3. about 142 degrees

Is momentum an invariant quantity?

An invariant quantity is one that has the same value, no matter which observer is making measurements. The space-time interval

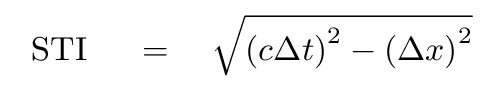
is an example of an invariant quantity.

Is kinetic energy an invariant quantity? Let's find out.

The Blue Man throws a ball (m = 0.2 kg ) at a speed of v = 20 m/s to the right.

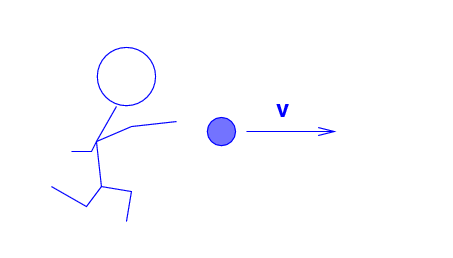
  Q:  What is the momentum of the ball,
      according to the Blue Man?

But the Blue Man and the ball are all travelling across the landscape at a speed of w = 50 m/s to the right, as measured by the Red Men.

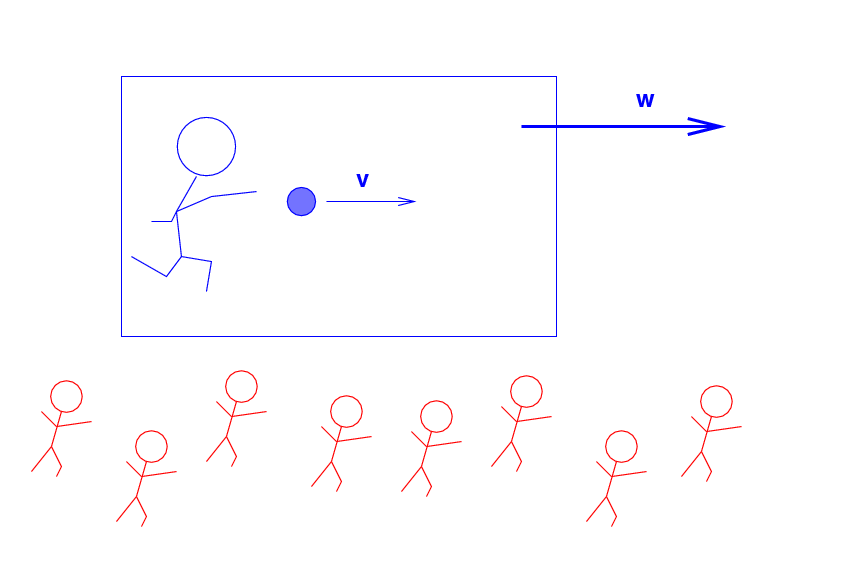
  Q:  What is the momentum of the ball,
      as measured by the Red Men?

For more information

• You might look at the notes to one of the other courses I teach, University Physics I for more details about kinetic energy and momentum in the non-relativistic regime.

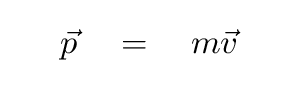
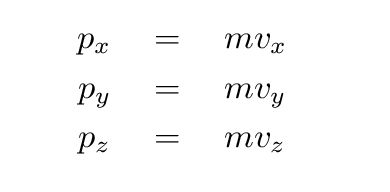
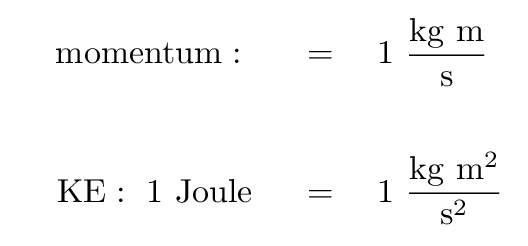
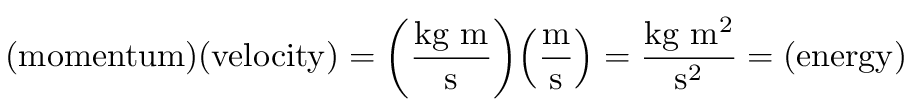
Copyright © Michael Richmond. This work is licensed under a Creative Commons License.