 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
You can read the original paper by Michelson and Morley:
Scientists knew a lot about waves. Sound waves travel through air, earthquake waves travel through the Earth. But what substance carried light waves? Physicists didn't know, exactly, but they figured that there must be SOME sort of substance. They gave it a name: luminiferous ether, which means "the stuff which carries light waves."
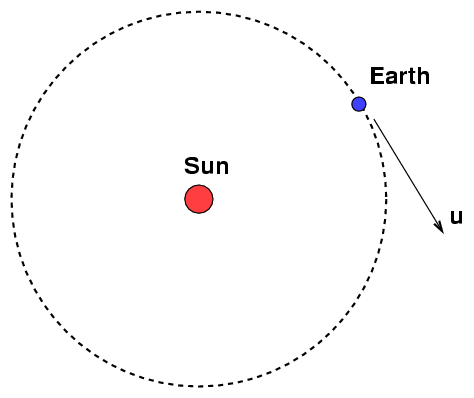
As the Earth orbits around the Sun, it must run through the ether. That will cause an "ether wind" w near the Earth's surface, blowing in the direction opposite to the Earth's motion u.

The Michelson-Morley experiment was designed to measure the extra time it took a light beam to travel "there-and-back" against the ether wind, compared to a light beam travelling "sideways across" the ether wind. The set up a light source, mirrors, and a telescope on a big slab of stone:
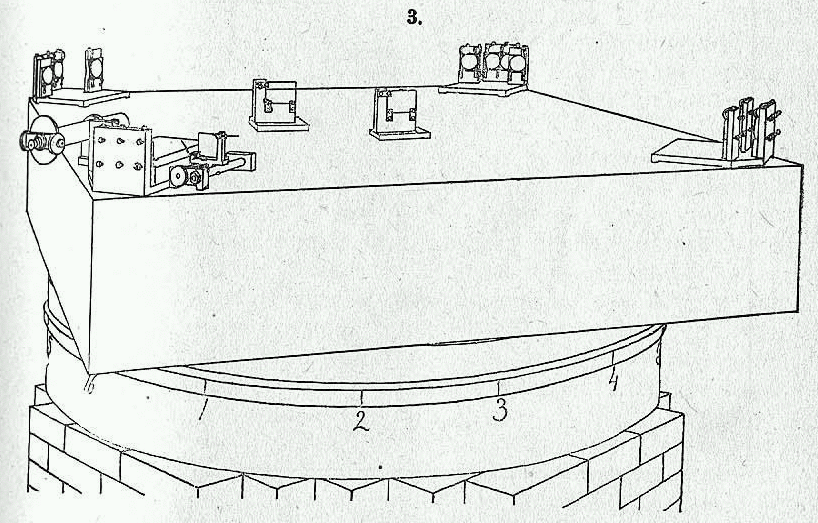
A single beam of light was split into perpendicular paths and sent bouncing back and forth four times across the stone. The two beams were then re-combined before they entered the telescope.

The idea was that one of the two beams would travel just a little bit faster than the other, so that when it arrived at the telescope, it would be slightly ahead of the other beam. Unfortunately, the difference in arrival time would be very, very, VERY small.
In the experiment,
D = 11 m half-distance along each leg
8
v = 3 x 10 m/s speed of light
u = 30,000 m/s speed of Earth in orbit
Q: How long should it take light to
travel with-and-against the ether wind?
Q: How long should it take light to
travel across the ether wind?
Q: What should the difference in time
be for the two light beams?

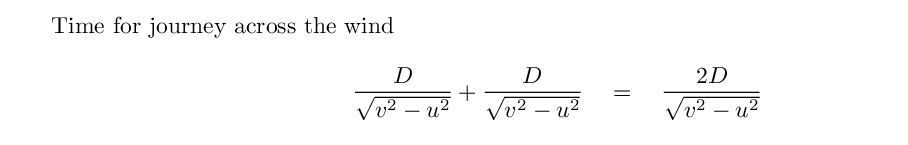
Hmmm. It would be nice if we could subtract one of these times from the other to yield a simple, easy-to-calculate result. Can we?
Yes, we can. All we need is
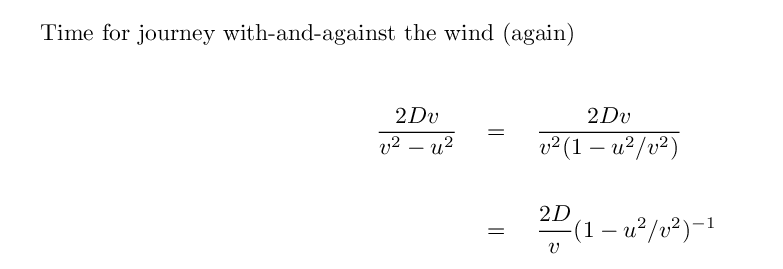
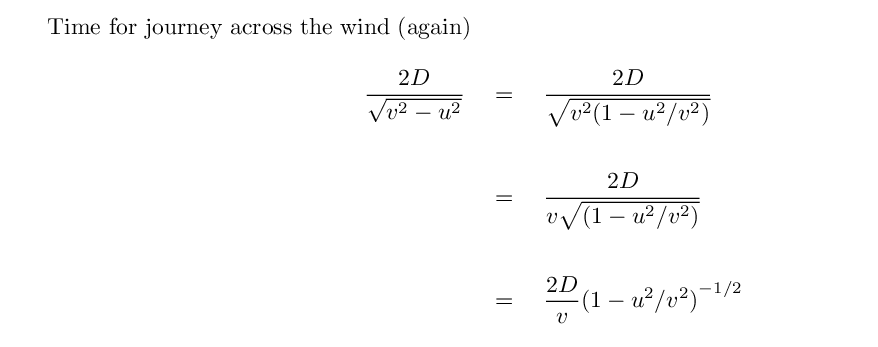
Now, the binomial expansion is a way of approximating the result when two numbers of very different sizes are combined in a common way.
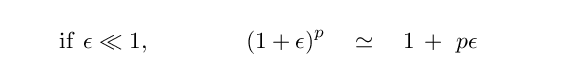
Q: Can you apply the binomial expansion
to the time for a beam to go with-and-against
the wind?
Q: Can you apply the binomial expansion
to the time for a beam to go across
the wind?
Q: What is the (approximate) difference in
times?
The difference, for the Michelson-Morley experiment, turns out to be small. Very small. Itsy-bitsy, in fact. On the initial run, the difference between the travel times along the two arms should have been

After they rotated the device by 90 degrees, the arm which was sideways to the ether would now be going with-and-against the wind, while the other arm would switch from there-and-against to sideways. This would cause the light beams to switch roles, so that the previous winner would now come in second place by the same difference. If Michelson and Morley compared the results from the two orientations, they ought to find a total difference which was double the difference in a single run:
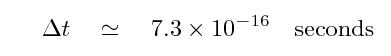
Michelson and Morley didn't have any clocks which could measure such tiny fractions of a second ... yet, with a clever trick, they COULD detect this tiny delay. The key is to watch very carefully as the two light waves interfere with each other as they come back together after their separate journeys.
Light often behaves like a wave (as you will learn in great detail in University Physics II), so let's review very briefly some properties of waves.
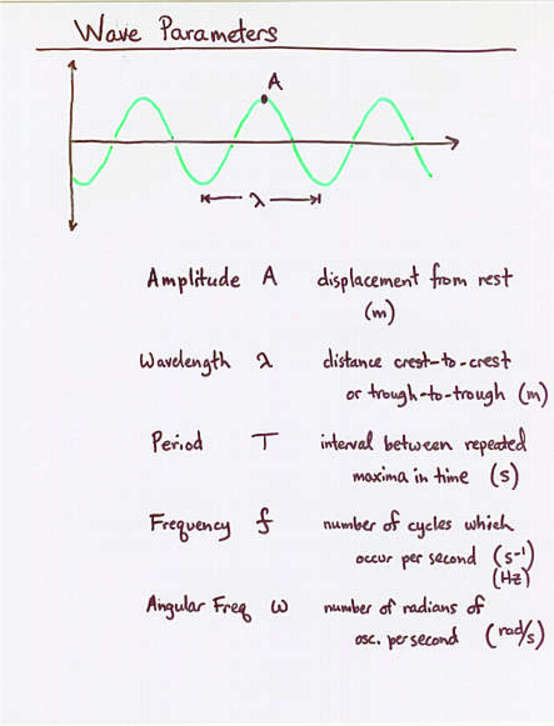
The waves in the MM experiment were light waves in the yellow region of the spectrum, with

All the waves were created by a single source, and so we may treat them as being (at least roughly) in phase.
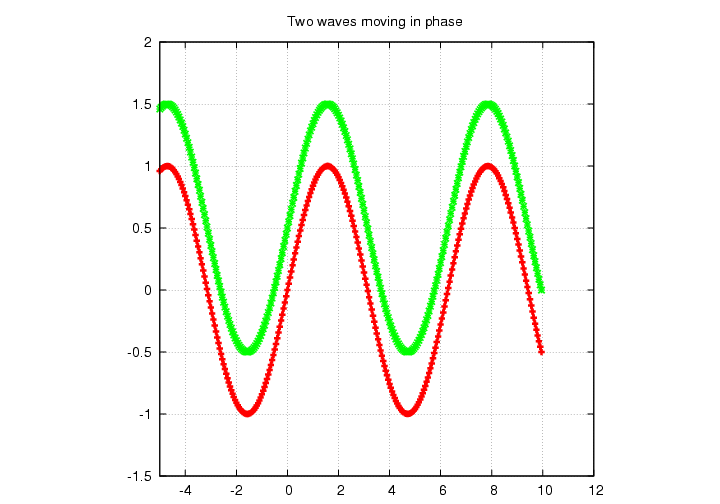
But one of the waves travelled along a journey that should have slowed it down just a little tiny bit, so that when the two waves met in the reticle of the telescope, they should have been slightly out of phase.
Q: One of the waves should have reached
the telescope first. How far ahead
should it have been? Express your
result in meters and nanometers.
Q: Now express the winning margin in terms
of the wavelength of the light.
In other words, express it like
"half a wavelength" or "6 wavelengths" or
something like that.
It turns out that when two beams of light are combined on a screen or wall after they have traversed different paths, they will interfere to create a series of bright spots. If you want to know why, you can look at notes on the double-slit experiment or some additional diagrams of the MM experiment. In any case, when Michelson or Morley looked at a small screen of ground glass in the telescope eyepiece, he saw a pattern of bright dots in a line, like this:

There was a scale on the glass, so that the observer could mark the position of one spot.

Remember that the whole apparatus was mounted on a big slab of floating granite, and was rotated very slowly -- it took about six minutes to make one complete rotation. Suppose that, at one moment, the apparatus happens to be oriented so that the ether wind is blowing at a 45-degree angle to the two legs:
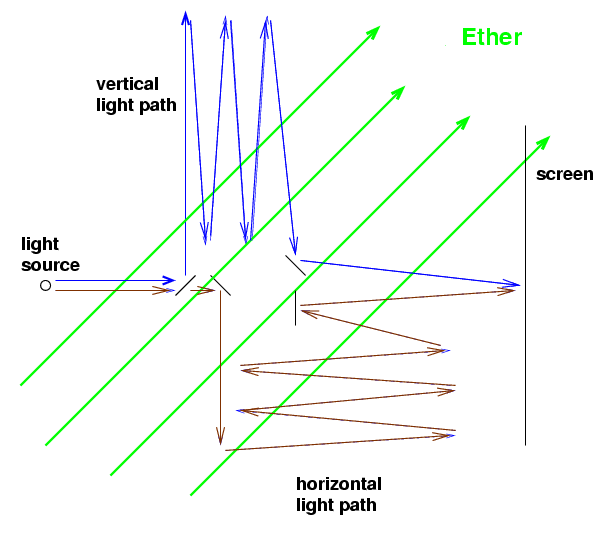
Q: Which light beam will reach the screen first?
Michelson notes that one of the spots of light lies exactly at the red mark. That means that the two light beams are meeting exactly in phase at the mark's location.

The big slab slowly rotates, so that the ether wind blows past it in a slightly different direction. After 15 degrees of rotation, the wind is now blowing like so:
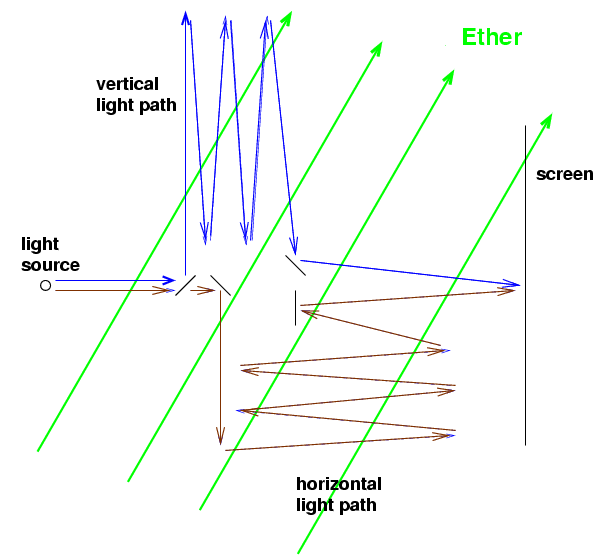
Now the "horizontal" light path is going more across the wind, while the "vertical" light path is going more with-and-against the wind. That means that the "horizontal" light beam will get the screen a little bit faster. At the position of the red mark, the two waves are slightly out of phase. That causes the pattern of spots to shift a bit. The size of the shift depends on the exact values of the speed of light and the speed of the ether wind. Based on their calculations, Michelson and Morley expected to see
approximate shift caused by 15 degrees of rotation of apparatus
= 1.2 x 10^(-16) seconds of delay between waves
= 3.7 x 10^(-8) m = 37 nm offset between waves
= 37 nm / 550 nm = 0.067 of one wavelength

Here's a closeup of the view through the telescope:

The scientists could easily see shifts in the position of the bright spots relative to the marks in the telescope's eyepiece. So, this interferometer allowed Michelson and Morley to detect the very, very, VERY small delays in time between two waves by its effect on the interference pattern.
Michelson and Morley expected to see a shift of this sort as they rotated their experiment on its stone table. They estimated the precision of their measurements to be about 2% of one wavelength of light. Based on the motion of the Earth around the Sun, they predicted that the maximum shift in position as the slab rotated ought to correspond to roughly 40% of one wavelength. Yet what they saw was
Huh?!?!?
Something had to be wrong -- in the experiment, or the theory. Michelson and Morley were confident that the experiment was not at fault. But, in that case, how to explain the lack of any shift with the rotation of the apparatus?
Almost two decades after the Michelson-Morley experiment, in 1905, Albert Einstein published a paper which explained its puzzling results. He simply stated there is no ether -- light is a special sort of wave which requires no medium to carry it.
Without the ether, there is no special frame of reference against which different observers can measure their motion. Einstein took this idea and ran with it, putting forth two postulates:
The second idea seems silly -- doesn't it? Consider a very concrete example:

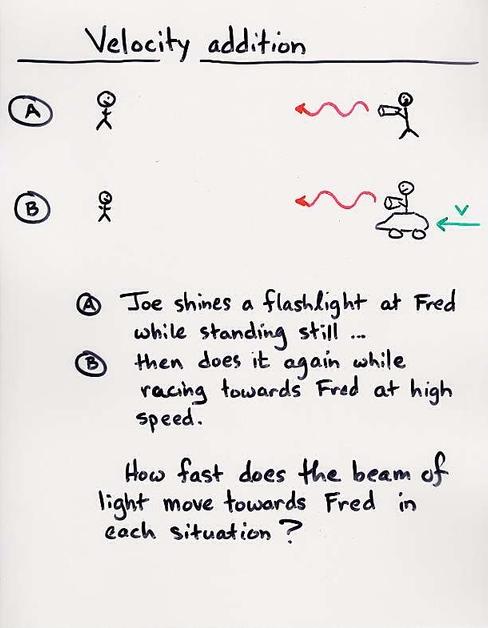
Is it really possible for the speed of light to be same to both observers? It doesn't match our everyday experience .... but we can still test the idea.


Alvager et al. measured the time it took gamma rays emitted by the moving pions to travel from detector A to detector B.
Distance from A to B = 31.45 m
time to travel from A to B = 104.9 ns
Q: What is the speed of the gamma rays
emitted by the pions?
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.