 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
This story is told in Spacetime Physics by Taylor and Wheeler, in Chapter 1. You can also find it in Professor Lindberg's notes, also in Chapter 1.
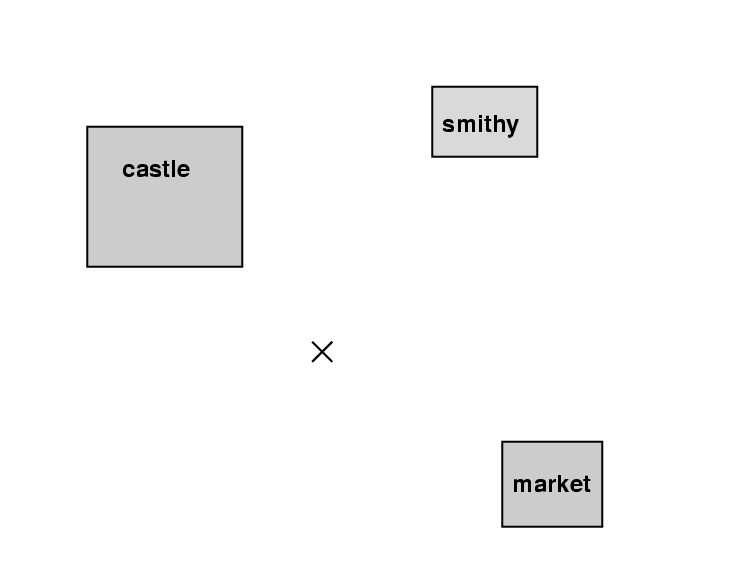
Once upon a time, long ago, there was a natural spring. People gathered around the spring and eventually settled into a town. Over the years, the town grew, but people continued to refer to the spring as "the center of town." The map below shows the spring, marked by an "X", and several of the largest buildings.

Prince Albert ordered his surveyors to measure the town and all its buildings. The Surveyors' Guild followed their revered ancestors in using two types of units when making measurements:
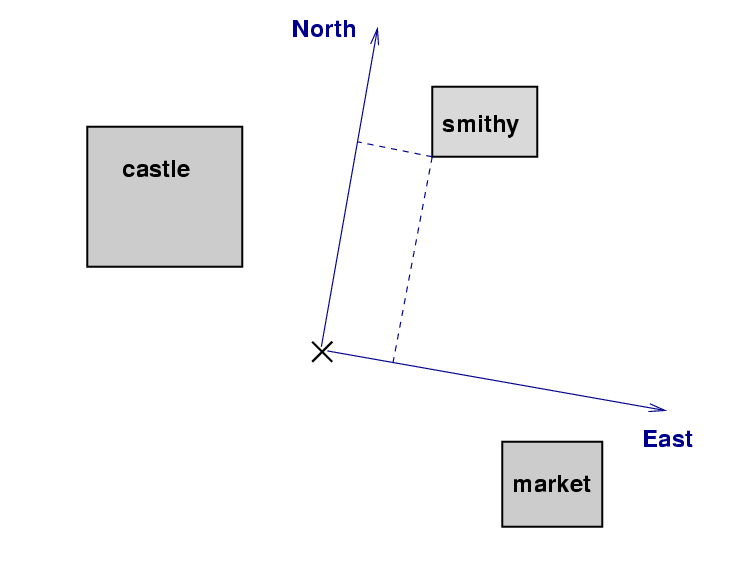
Now, there were two groups in the Surveyors' Guild: one faction went out in the daytime and used magnetic compasses to locate North. Their map of the town looked something like this:
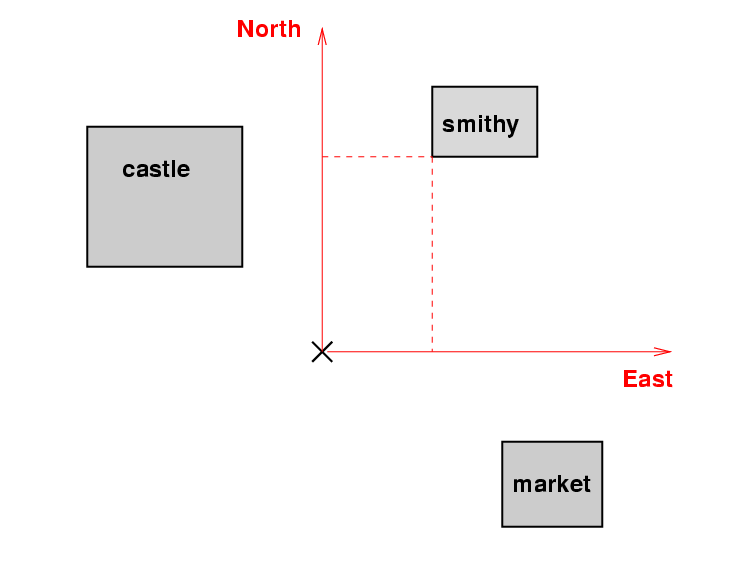
The other faction did their work at night, because they counted on Polaris, the North Star, to mark the position of North. Their map of the town looked something like this:
Each group of surveyors presented Prince Albert with both a map and a list of the locations of all buildings in the town. The smithy, for example, was listed like so:
Night team Day team
--------------------------------------------------------
about one-and-half miles North about one-and-a-half miles North
about 2500 feet East about 2000 feet East
---------------------------------------------------------
Q: Are these two locations the same? Q: Does it matter?
Over the next century, the town grew. The surveyors invented new techniques to measure distances, using long pieces of metal tape, carefully calibrated wheels, and small telescopes. One hundred years later, Albert's grandson, Prince William, asked his surveyors to record the positions of all the structures in the city again. As before, he received two maps and two sets of positions from the Daytime Team and the Nighttime Team. Their measurements for the smithy now looked like this:
Night team Day team
--------------------------------------------------------
1.52 miles North 1.58 miles North
3000 feet East 1950 feet East
---------------------------------------------------------
Q: Are these two locations the same? Q: Does it matter?
"Such a discrepancy is unacceptable in this modern era," declared the Prince. "Figure out why these two sets of measurements don't agree, or else!"
One of the junior surveyors, Fred, pondered the problem late into the night. He came up with a radical idea that might help: forget about tradition, use a single set of units for both directions. The next day, he determined that
1 mile = 5280 feet
He could now write the location of the smithy using feet in both directions. What are the new North positions he computed?
Night team Day team
--------------------------------------------------------
8026 feet North 8342 feet North
3000 feet East 1950 feet East
---------------------------------------------------------
Fred stared at these positions over and over again, wondering if there is any connection between them. "It's the same building," he thought, "how can it have two different locations?"
One day, he remembered something from a geometry class: the relationship between the sides of a right triangle. Could a line drawn from the spring to the smithy be the same in both coordinate systems?
He computed a quantity he called "distance":
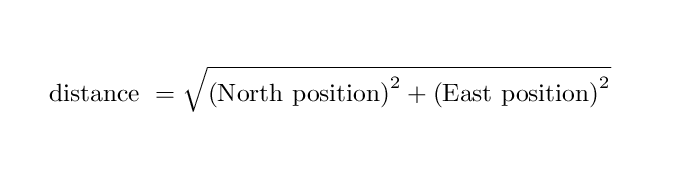
Q: What is the distance in the Daytime coordinate system? Q: What is the distance in the Nighttime coordinate system?
"Aha", he cried, "this must mean something!" He went on to calculate the "distance" between the spring and other buildings in the city, and found that for every building, the distance was the same in both coordinate systems. Fred discovered that the Euclidean distance is an invariant quantity in the surveyors' world. In other words, the distance between two points will be the same, no matter who measures it.
What does all this have to do with special relativity? Quite a lot, as you will find out over the next few weeks.

Just as the surveyor realized that for some purposes, it was much simpler to convert two types of units -- miles and feet -- into a single unit -- feet, you will discover that for some purposes, it is much simpler to convert the mix of seconds and meters into a single unit -- usually meters -- before working through a puzzle.
Just as the surveyor found that one particular combination of measurements, the "distance", was the same according to two different groups of observers, so you will find that one particular combination of measurements, the "space-time interval", is the same according to any observer in an inertial frame.
By the way, do you see anything that bothers you about the definitions of "intervals" in the table above?
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.