Intelligent observers

The rules of special relativity only apply to intelligent observers. What defines intelligence, in this particular situation? Perhaps an example will suffice.

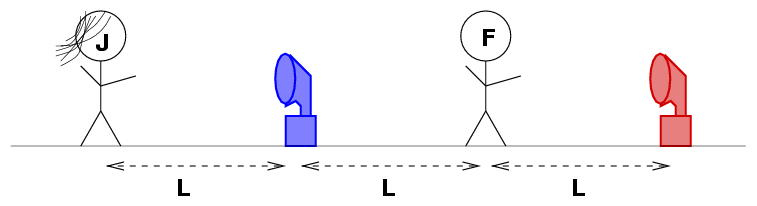
There are two big horns, one red and one blue. Fred stands exactly in between the horns, an equal distance from each one. Jane stands off to the left.

The two horns each produce a lound "BEEP!" Jane hears the BEEPs occur at just about the same time. Fred hears the red horn long before the blue horn.

Jane concludes that the two horns must have honked simultaneously, because she heard the two noises simultaneously.
Fred concludes that the two horns must not have honked simultaneously, because he did NOT hear the two noises simultaneously.



  Q:  Is either person an "intelligent observer"?
      

  Q:  If so, which one?

Right. In this relativistic context, an intelligent observer is one who is aware of the time it takes for signals of various kinds to travel from one place to another.

Sychronizing metersticks

Intelligent observers will verify that their space-measuring devices are consistent with the devices of their colleagues. For example, consider the humble meterstick. Both Fred and Jane have metersticks. How can they be sure that their measurements of length are consistent?

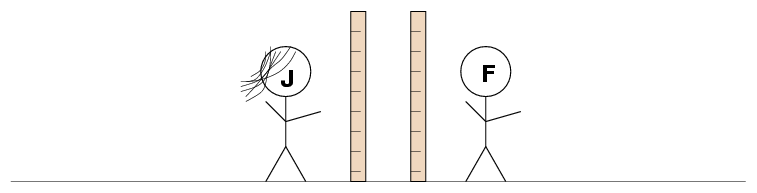
This is pretty obvious, I hope. Jane and Fred carry their metersticks and walk towards each other. It is safe to assume that the act of being carried will not permanently change the properties of each stick (at least as seen by Jane and Fred). When they meet, they hold their sticks upright, very close together.

Sychronizing clocks

Intelligent observers will verify that their time-measuring devices are also consistent with those of their colleagues. However, note that clocks are more complicated instruments than metersticks. The scientists must worry about two aspects of each clock.

the rate at which it runs
the zero-point, or reading at some particular time

Verifying that the rates are the same is not so difficult. Fred and Jane carry their clocks as they walk towards each other. When they meet, they place their clocks together and watch as Jane's ticks N times. If Fred's also ticks exactly N times during this interval, then the clocks have the same rate.

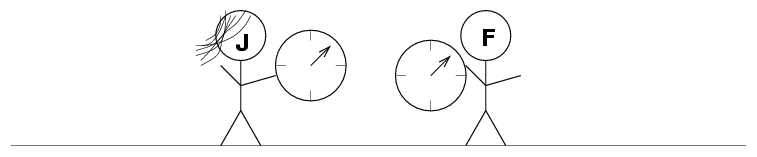
Yes, they may have to wait for a long time, so that N becomes a large number of ticks, but that just takes patience.

After verifying that the clocks do run at the same rate, Fred and Jane may walk back to their original positions. Now, while they moving, there is no guarantee that their clocks will run at identical rates; but once they stop moving, and are once again stationary relative to each other, it's safe to assume that the clocks will once again be running at the same rate.

BUT ... while they were walking back to their homes, their clocks may have been slower than usual. The two clocks may have fallen out of sync. How can these two separated observers synchronize their clocks?

Fred comes up with an idea. He says, "I'll use my handy telescope. Jane, hold up your clock so that its face points in my direction. I'll just focus on it ... ah, there we go.

I see that your clock reads 21 right now, so I'll set MY clock to 21, too. There! Now our clocks are synchronized."



  Q:  Is Fred being intelligent?

Jane comes up with an idea. She says, "First, let's measure the distance between your place and mine." Jane uses her meterstick to measure the distance as she walks slowly from her home to Fred's home. She finds that the distance is L = 20 m.

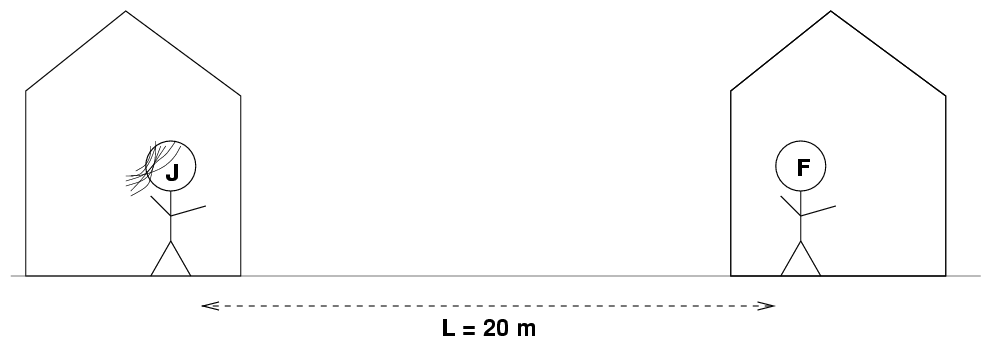
She tells Fred, "I'm going to go back home now. But tomorrow, when the time is exactly t = 50 m on my clock, I'm going to turn on my bright red flashlight."

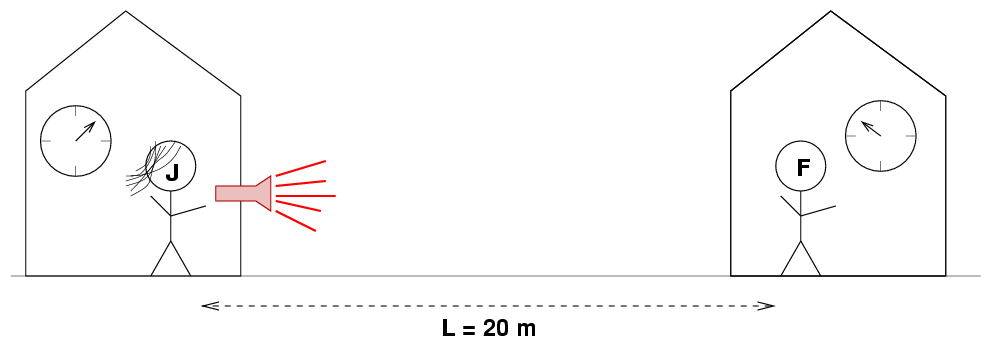
Fred replies, "Okay, I understand. Tomorrow, as soon as I see the red light coming from your house, I'll set my clock to t = 50 m, and then our clocks will be synchronized."



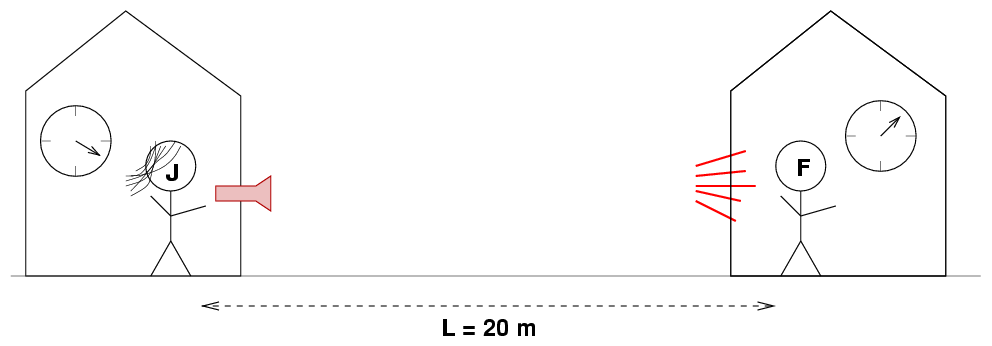
  Q:  Is Fred being intelligent?

"No, no, no!" cries Jane. "That won't work. What you have to do is to wait for the red flash, and then set your clock to a different time."



  Q:  When Fred sees the flash, to what
      value should he set his clock?

The importance of teamwork

Big Joe goes to the ballpark. He has a watch and a meterstick. His job is to watch batting practice and measure the time and location of each home run.

If Big Joe is NOT intelligent, he may try to do the job like this:

But if Big Joe is an intelligent observer, he will realize that a single person just can't do this job. The only way to make accurate measurements is to incorporate an army of helpers, the Little Joes. Each member of the team has

a meterstick
a watch, verified to run at the same rate as Big Joe's watch, and which has been synchronized with Big Joe's watch
a piece of paper and a pencil

The Joes line up across the ballpark, so that each person is spaced one meter apart. They stand motionless and wait for balls to fall in front of them. When a ball hits the ground, the nearest Joe reads the time from his clock, the position from his meterstick, and writes them down on a piece of paper, together with his own name and position in the line.

At the end of the day, the Joes pass their records to Big Joe. Big Joe can then reconstruct the exact location of each event at his leisure.