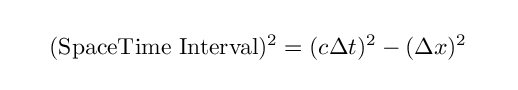
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Special relativity allows one to understand the relationship between observations of the same phenomena made by different observers. However, there are a few limitations: for one thing, the rules of special relativity apply in a precise manner only to certain types of events measured by the observers. Specifically, an event must
Why are there quotation marks around tiny? Because it depends on the scale of the situation. Consider turning on a flashlight. From our point of view as humans, the flashlight bulb is a pretty small thing, so if we measure the event Joe turns on the flashlight, we'd say "yes, that's an action which occurs in a tiny, specific location." On the other hand, if a colony of E. coli bacteria were making the measurements, they would disagree: the filament of the flashlight bulb would stretch for millions and millions of their body lengths. They couldn't use bacteria-sized metersticks to measure the entire filament growing hot and glowing, and so they might say, "no, that's not a good example of an event."
So, when you are considering different situations, ask yourself, "who is doing the measuring? What tools is he using? Over what scale does the action take place?"
Suppose that the students in this class are the ones making measurements, and that they are equipped with metersticks and ordinary wristwatches. Which of these qualifies as a good event from the standpoint of a physicist?
In ordinary life, we use different units to measure intervals of space -- meters, feet, miles -- and intervals of time -- seconds, days, years. When it comes to performing relativistic calculations, it will sometimes help to adopt a single type of unit for all measurements. For example, if we want to compute the space-time interval between two events,
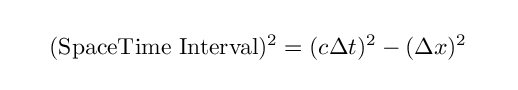
we could simplify if we used the same units for distance intervals and for time intervals. Then we could write
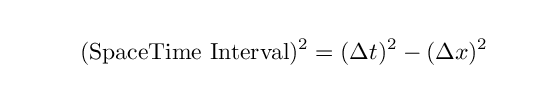
For example, consider the following situation.
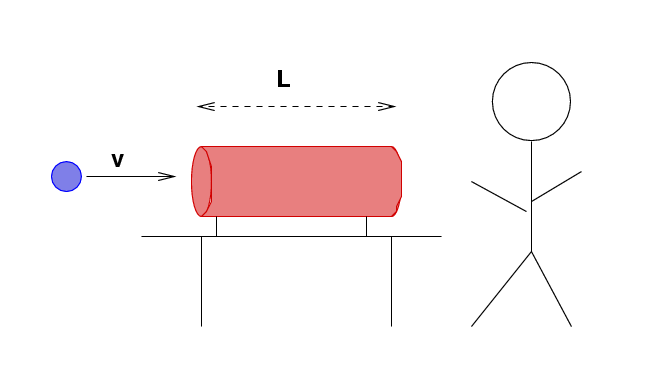
Fred sets up a tube, L = 5 m long, on a table in his lab. He places it directly into the path of his particle accelerator. A proton moving at v = 0.5 c flies towards the tube.
Fred's tube has devices at each end which can measure exactly the moment when the proton passes by. Fred decides to label things like so:
Event 1: Proton enters tube
Event 2: Proton leaves tube
Q: Are these good examples of "events"?
Q: What is the difference in time between
these two events?
Q: What is the difference in position between
these two events?
Q: What is the space-time interval between
these two events?
We can represent the events in the lab with an event diagram, which shows positions on the horizontal axis, and times on the vertical axis. In the diagram below, which units have I chosen?
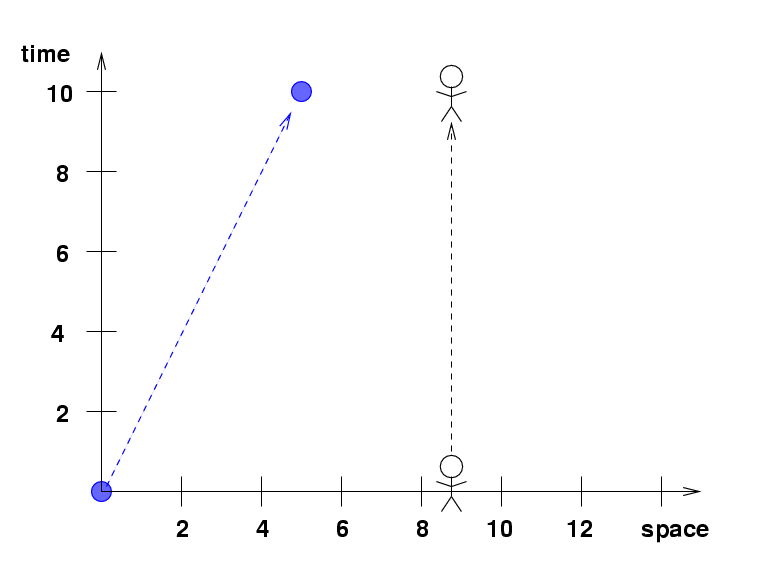
Hmmmmm. Before we leave this particular experiment, let's look at things from a different point of view. All the measurements we've considered up to now have been made by devices sitting still in Fred's lab. Suppose what we look at things from the PROTON'S point of view.
The proton is sitting quietly, looking at its watch, as the table and tube coming flying towards it at a speed of v = 0.5 c . The proton notes when the tube's open end engulfs it, and also when the other end of the tube moves past it and leaves it back in open space again.
Q: Are these good examples of "events"?
Q: According to the proton, what is the
difference in position between these two events?
Q: According to the proton, what is the
space-time interval between these two events?
Q: According to the proton, what is the
difference in time between these two events?
Gosh, that's strange. Look at the time invervals between the two events:
according to Fred according to the proton
------------------------------------------------------
They are not the same. What does that mean?
Let's consider a very different situation, for which very different units are appropriate. The Federation of Earth decides to send a spaceship to the colony called "Della", which orbits around the star Alpha Centauri. The spaceship travels with a constant speed v = 0.9 c .
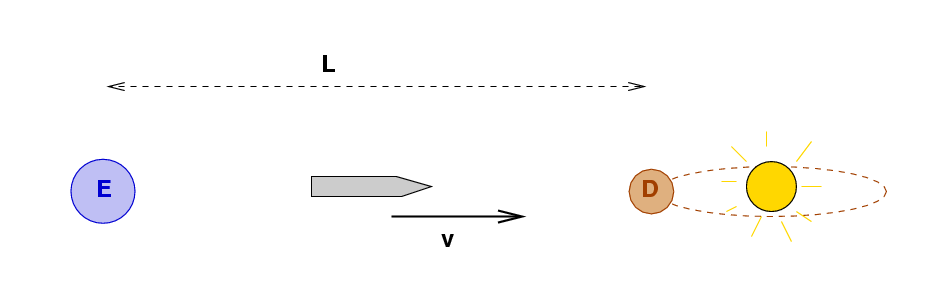
Alpha Centauri is very, very, VERY far away from the Earth. If we express the distance in meters, we find
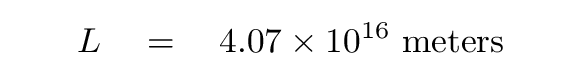
That's a poor choice for units in this case. A better choice is to use seconds, or, even better, years. The number will be nice and small, easy to say, and, as you will see, it will also be useful when we ponder the consequences of the situation.
Q: What is the distance between the Earth and
Della, expressed in years?
Q: How long does it take the spaceship to
travel from Earth to Della?
Q: What is the space-time interval between
these two events:
A. spaceship leaves the Earth
B. spaceship arrives at Della
(are these good examples of "events"?)
Now it's your turn to make a space-time diagram. Please draw on one sheet of good graph paper a diagram which shows intervals of distance on the horizontal axis, and intervals of time on the vertical axis. Be sure to
You can see my own diagram on graph paper if you like.
Hmmmm. Before we leave this example, let's look at the trip from the point of view of the captain of the spaceship. Before he leaves the Earth, he very sensibly sets his clocks to match those of the Federation spaceport. He keeps track of the following events:
Q: According to the captain, what is the
difference in position between these two events?
Q: According to the captain, what is the
space-time interval between these two events?
Q: According to the captain, what is the
difference in time between these two events?
Gosh, that's strange. Look at the time invervals between the two events:
according to Earth according to the captain
------------------------------------------------------
They are not the same. What does that mean?
As you have probably guessed by now, even though the space-time interval between two events is the same, no matter which (inertial) observer measures it, the components of the interval may not be the same. In these examples, you have seen that two different observers measure quite different time intervals between the same two events.
Is there one time interval which is the "right" one? NO -- all the time intervals are correct, according to their observers. However, there is one interval which is special, in a way. Look at the equation again:
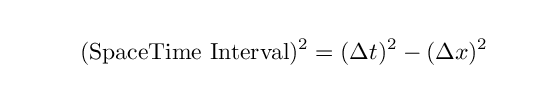
For any particular pair of events, the space-time interval is fixed. The space and time components may have any sizes, as long as those sizes combine to yield the space-time interval. The very smallest possible value for the time component will occur when the space component is zero:
This interval will be measured by an observer who sits still at the same location as both events. We call this minimum possible time between two events the proper time.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.