Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Objects which remain motionless will always have the same space coordinate. Therefore, as time goes on, they will appear to make vertical lines in a space-time diagram.
What about an object which moves? Fred starts at location x = 2 m at time t = 0 m, but then walks to the right with a speed of v = 0.2 c .
Q: Where will Fred be at time t = 5 m?
Q: Where will Fred be at time t = 10 m?
Q: What is the slope of the line Fred
makes in the space-time diagram?
Jane starts at location x = 10 m at time t = 0 m. She walks to the left at velocity v = 0.5 c.
Q: Where will Jane be at time t = 5 m?
Q: Where will Jane be at time t = 10 m?
Q: What is the slope of the line Jane
makes in the space-time diagram?
At time t = 1 m, a lightbulb sitting at x = 0 m suddenly lights up. Light rays fly outwards in all directions from the bulb.
Q: What are the slopes of the lines
made by the light rays in this
space-time diagram?
Do you see the pattern here? What is the general rule for the slope of a line representing an object in space-time diagrams?
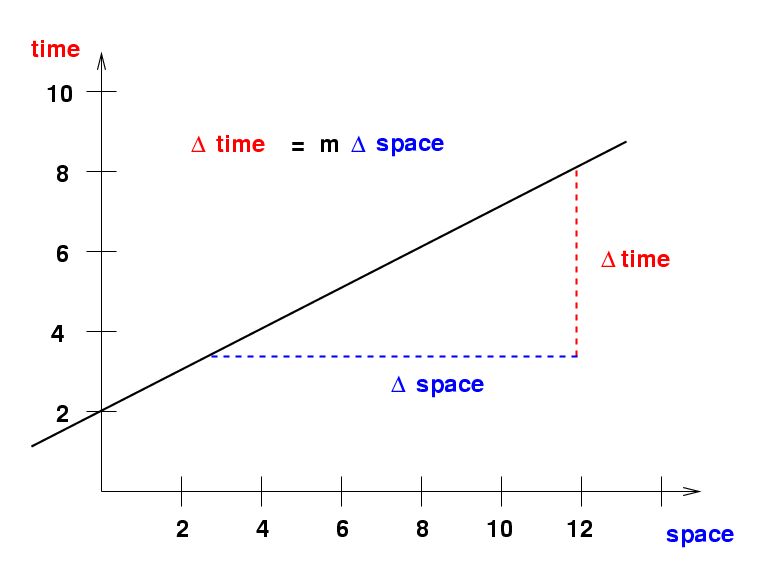
If we choose to describe the slope in the usual manner, as the relationship between the quantity on the horizontal axis and the quantity on the vertical axis, like this:
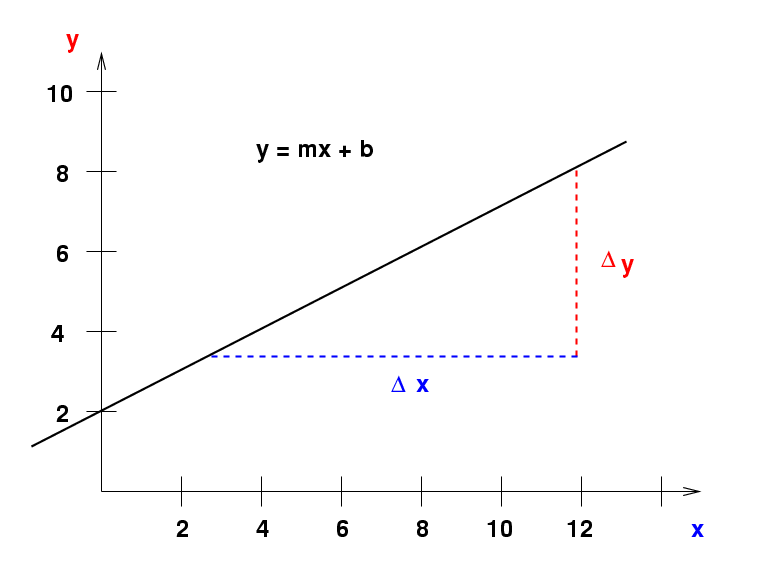
then the slope of a line in the space-time diagram is
change in time 1
slope = ---------------- = -------
change in space speed
A group of students are all sitting at home, all doing their homework.
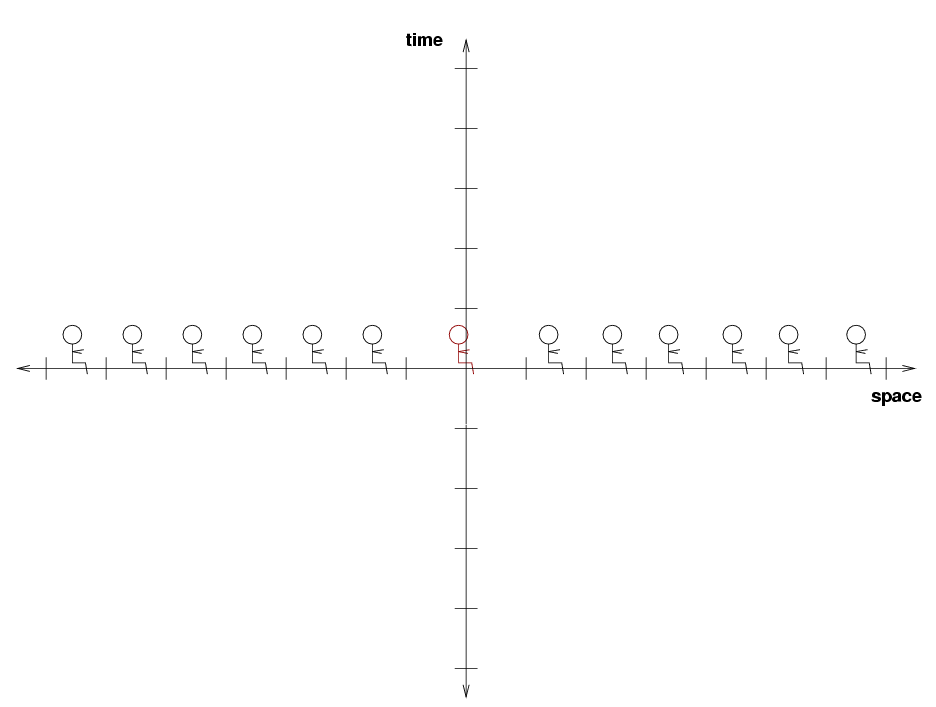
Under ordinary circumstances, we could draw a space-time diagram representing these students over the next few minutes ....
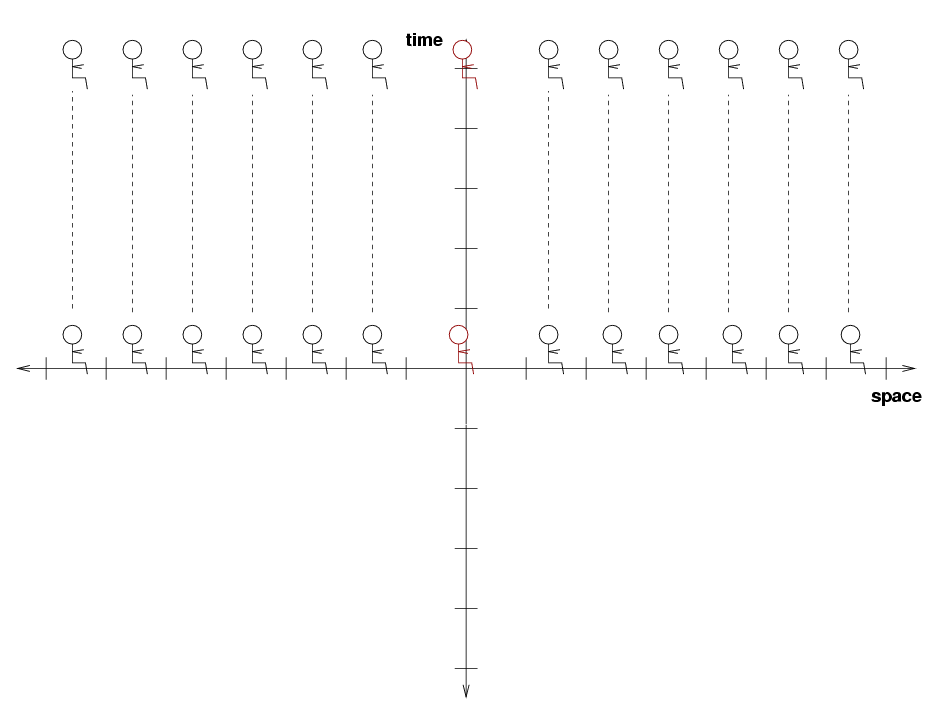
However, these are not ordinary circumstances. Some months ago, a disgruntled employee at a cell-phone factory installed a hidden program onto all cell phones: at exactly 11:23:00 PM tonight, every cell phone in the world will start to play It's a Small World at full volume, repeating endlessly.
At 11:22:45 PM, Joe notices something written on the napkin he picked up at a cafe earlier that day. It's a full confession from the disgruntled employee. Joe realizes that in just 15 seconds, all his friends will suffer agonizing torture.
Joe sends a special emergency message to all his friends using his walkie-talkie. "If they hear this in time," he thinks, "they will be able to turn off their phones before the song begins!"
Q: Can he warn them in time?
It turns out that Joe can warn SOME of his friends, but not all of them. The fastest way to send this message is via a burst of radio waves, travelling at the speed of light. Even at the speed of light, however, the message will not be able to reach all of Joe's friends before the 11:23:00 PM deadline.
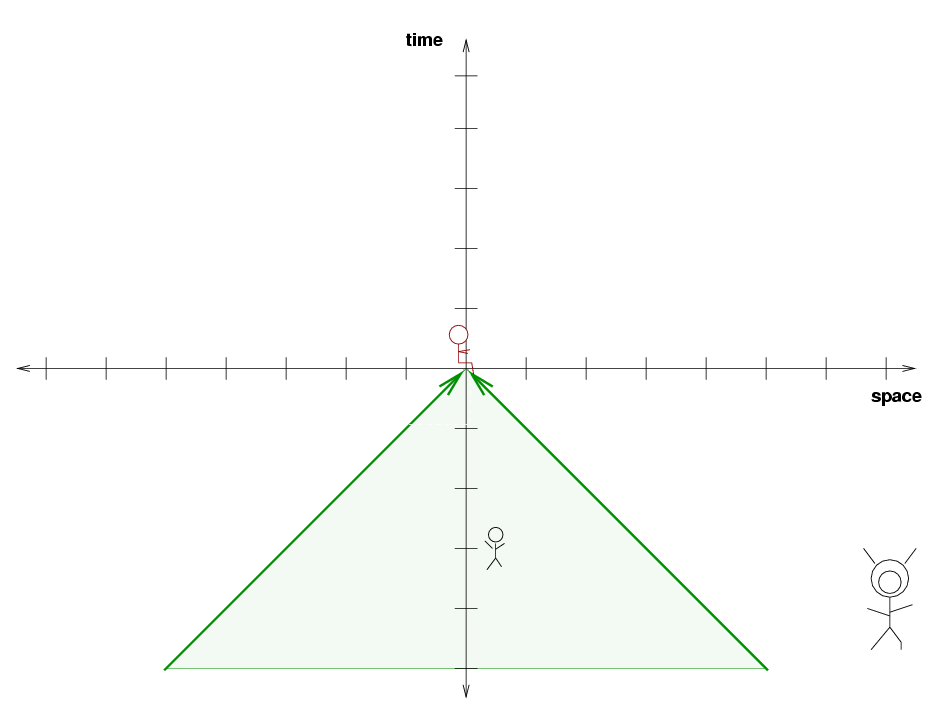
You can see that there is a region of the spacetime diagram which lies within the light beam's grasp over the next 15 seconds. Joe's message can reach people who live within this region; we can describe it as Joe's "region of influence" over the next 15 seconds.
If you imagine making a three-dimensional graph which shows two spatial dimensions on horizontal axes, and the time dimension on the vertical axis, then a light beam leaving Joe's position at the origin would define a cone with a circular horizontal cross-section moving upwards. Therefore, this region of Joe's influence is sometimes called Joe's future light cone.
People whose world lines lie outside this region will not be able to receive any signal from Joe. By the same token, those same people will not be able to send a message of their own to Joe in the next 15 seconds, either. There can be no communication at all between Joe and these unlucky people.
As time goes on, Joe's region of influence expands; in fact, it expands at the speed of light. If Joe waits long enough, he can send a message to nearly anyone ...
If Joe looks into his recent past, he'll see that there are only a limited number of people who have been able to influence HIM. In the past 60 seconds, for example, his brother sent him a text message: "Mom says you have to take out the trash tonight!" Because his brother lives nearby, the message was able to reach him.
However, if his friend Bob, who is on a field trip to Mars, had tried to send him a message 60 seconds ago, that message would not have reached him yet. Bob is too far away for any of his recent actions to influence Joe in any way. Another way to describe this is that Bob is outside Joe's past light cone.
Note that this region of events which may have affected Joe grows the farther back in time we look. If Bob on Mars had sent a message to Joe yesterday, then it could have reached him by now.
Let's practice using space-time diagrams. Please take out a piece of graph paper and draw a set coordinate axes centered on the paper. Make sure that the horizontal axis goes from at least -15 to +20 ns, and the vertical axis from at least -10 to +20 ns.
Let's adopt nanoseconds (ns) as the units for both time and space.
Now, consider the following actors and events.
How can we write an equation to describe the path of each actor?
Please draw all the actors on your space-time diagram. Label them carefully.
Now figure out when and where each of the following events occurs. Mark it clearly on your diagram.
You can look at my graph and my solutions if you want. I chose to write equations of the form
1
t = (-------) x + b
speed
It is also possible to represent the same lines in the form
x = speed * t + d
Either way is fine -- you'll come up with the location of intersection.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.