 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Suppose that Einstein is right: the speed of light is measured to be the same by observers in all inertial frames. What does that mean? Well, consider a few simple situations.
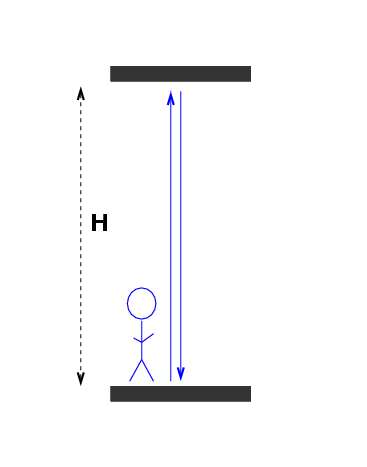
Blue Man stands in a room. He decides to measure the height of his room by bouncing a light beam off the ceiling, and measuring the time it takes to return.

The height of the room is L, and the light beam travels at c, so the time it takes for the beam to go there and back is
2*L
t(blue) = -----
c
So far, so good.
Now, consider another observer: Red Man. Blue Man is in a frame which zooms past Red Man at a constant velocity v. As Red Man watches the Blue Man and his room go by, he also measures the distance travelled by the light beam.

What distance does the light beam travel, according to Red Man?
 Viewgraph 1
Viewgraph 1
Now, if Red Man and Galileo were standing together and watching the beam, Galileo would say,
Behold! The room moves past us sideways at speed v, carrying the light with it. So the light beam travels faster than usual: it has a vertical component of 300,000,000 m/s, plus a horizontal component of v, and thus a total speed ofspeed of light beam = sqrt ( 300,000,000*300,000,000 + v*v )The time it takes to reach the ceiling of the room and bounce back is, naturally, the same2 * L time to go and return = ------- cthat Mr. Blue Man measured.
But if Einstein were present, he would disagree:
Actually, the light beam travels at exactly the same speed,
speed of light beam = 300,000,000 m/s
from both our point of view, as we watch the room fly past
us, or from Mr. Blue Man's point of view, inside the room.
It is the time taken to make the trip which changes,
not the speed of light.
So, according to Einstein, how long does the light beam take to make its trip, as seen from the ground with Red Man?
 Viewgraph 2
Viewgraph 2
 Viewgraph 3
Viewgraph 3
 Viewgraph 4
Viewgraph 4
 Viewgraph 5
Viewgraph 5
 Viewgraph 6
Viewgraph 6
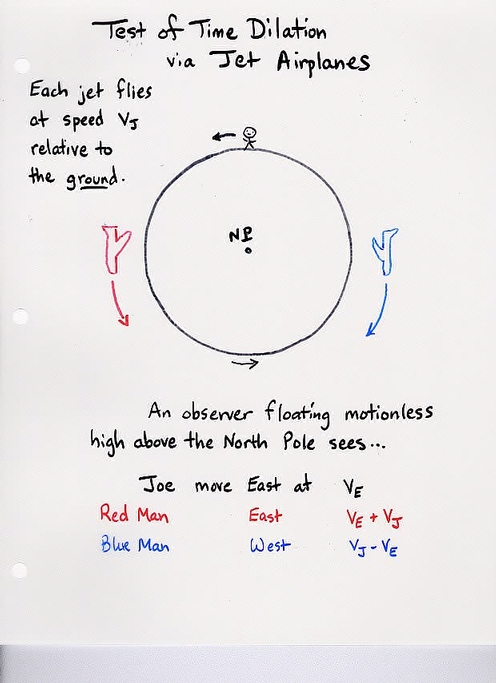
Assume that planes fly at about 500 mph = 250 m/s
relative to the ground.
Q1: How long does it take a plane to fly around
the world?
Q2: According to the stationary observer floating
above the North Pole,
what is the gamma factor for Joe?
what is the gamma factor for red plane?
what is the gamma factor for blue plane?
Q3: What is the difference between Joe's watch
and the red plane's clock when they meet?
Q4: What is the difference between Joe's watch
and the blue plane's clock when they meet?
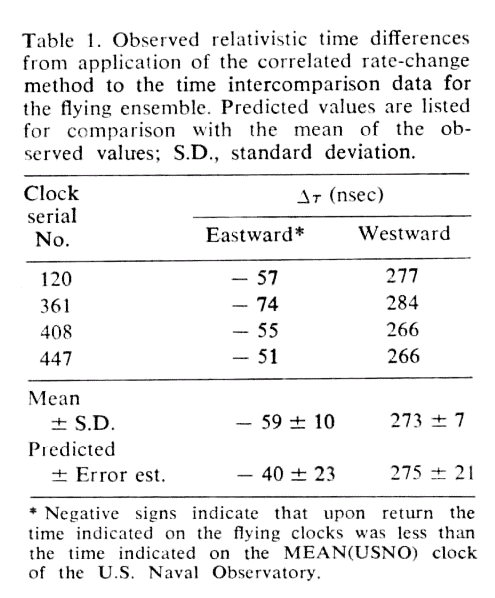
Calculating the gamma factor for ordinary speeds v much less than the speed of light can be tricky; some calculators can't handle numbers which are very, very close to 1. Read this example of calculating gamma for a few tips.



 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.