Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
It's not only TIME which behaves in new ways in the relativistic realm -- even the LENGTH of an object appear different to observers in different inertial frames. Let's look at how that might happen.
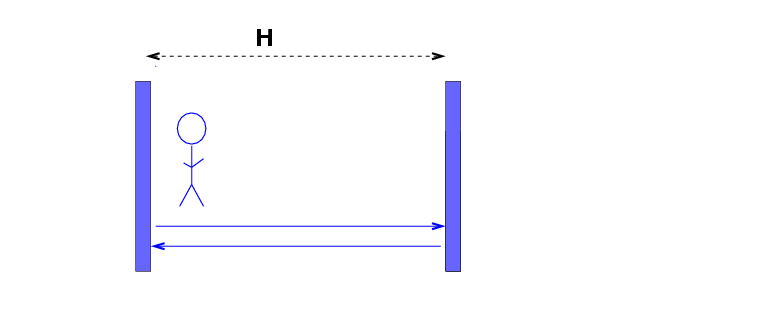
The Blue Man lives in a Blue Room. He places a laser on the left wall, pointing straight to the right wall, which is H = 10 m away. There's a mirror on the right wall. The Blue Man runs an experiment in which he measures two events:
According to the Blue Man,
1. What is the space interval between these
two events?
2. What is the time interval between these
two events? Call this time interval tb.
Now, the Blue Man and his Blue Room are flying across the landscape at a very high speed. They fly past the Red Man and his army of Red Minions, all of whom have metersticks, notebooks, and synchronized watches. The Red Army observes this same experiment, and makes its own measurements. The Red team breaks the experiment into two pieces. First, the laser beam makes its way from the left wall to the mirror in a time interval t1.
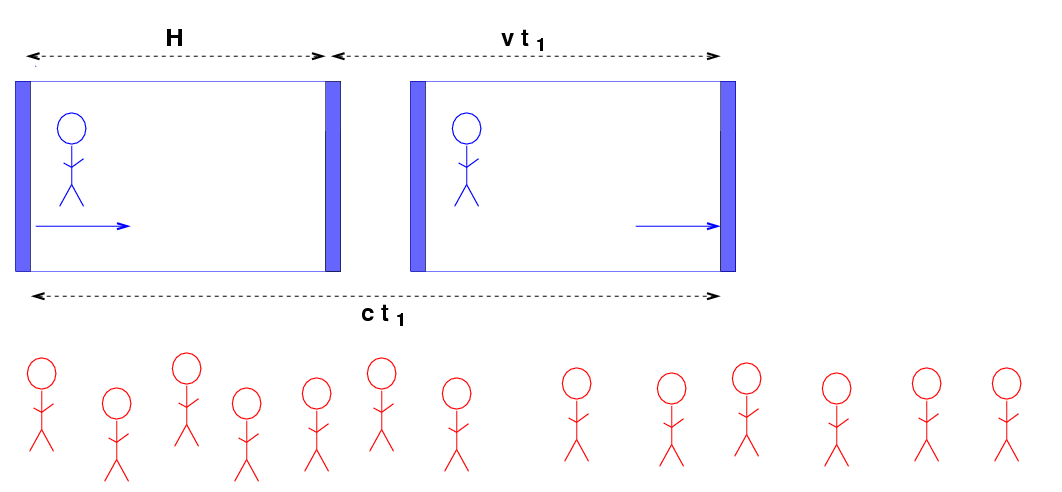
Q: Write an expression for the time t1
measured by the Red Team, in terms
of c, v, H.
As the Red Men continue to watch and make their measurements, the laser beam shoots back towards the left wall. But since the left wall is coming towards the beam, it doesn't take quite so long for the beam to reach the wall this time. The Red Army determines that a time interval t2 occurs between the reflection and return.
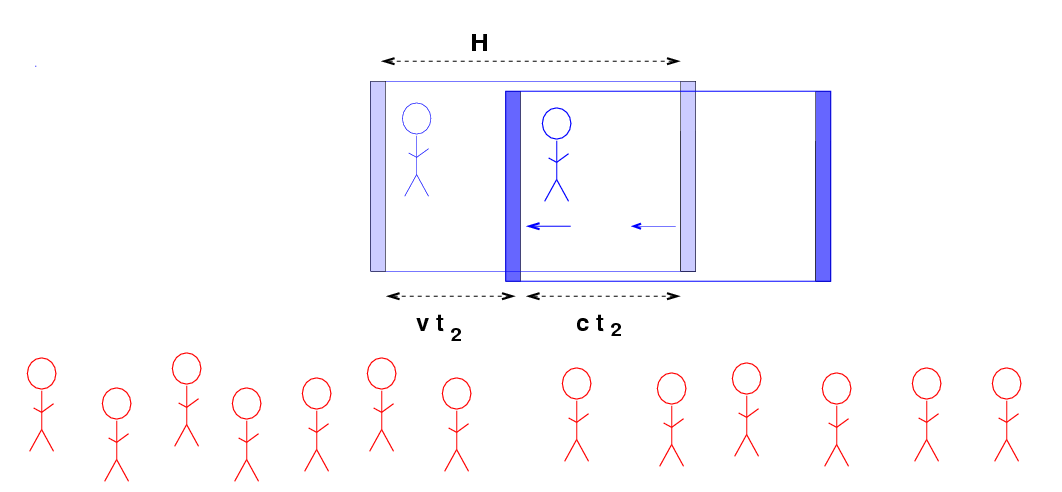
Q: Write an expression for the time t2
measured by the Red Team, in terms
of c, v, H.
Now, the total time interval between the two events -- laser beam leaves left wall, and laser beam returns to left wall -- as measured by the Red Army must be
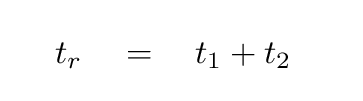
Q: Write an expression which shows the total
time interval measured by the Red Men
in terms of c, v, H.
Find a way to write the Red Team's
total time interval in a form which looks
like
2 H
----- * (something)
c
So, according to these two sets of inertial observers, the time interval between two events is not the same. Well, that's no surprise. As we saw in the previous lecture, the two time intervals are connected by the "gamma" factor.
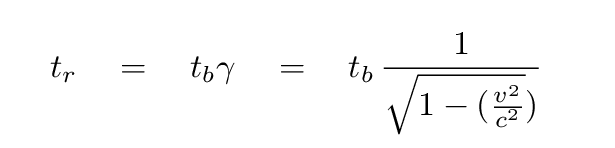
Q: Look at your expressions for the times
tb and tr.
Is the time interval measured by the Red Men
longer by a factor of gamma?
Something must be wrong. Is it possible that the Blue Man can ruin all the special relativity just by pointing his laser at the wall instead of the ceiling?!
Let's look at these times more closely.
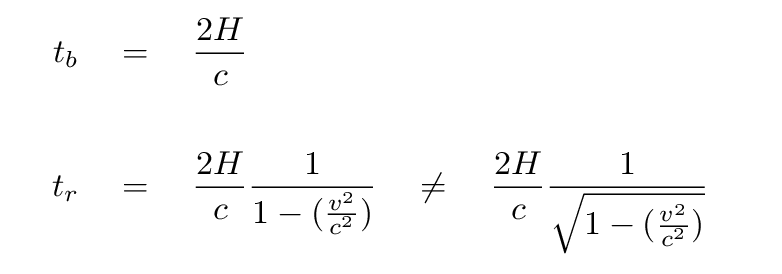
Is there any way we can make the red time equal to gamma times the blue time? Hmmmm..... What if we were to postulate that the width of the room in the direction of motion, H, wasn't the same in the two reference frames? If there are two different values for H, then maybe we could make the red time interval equal to the blue time interval times gamma.
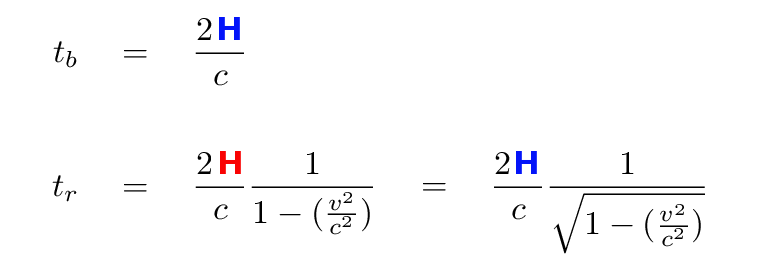
Q: What value must the Red Team's measurement
of H have in order for the
times to come out right?
But what does that mean? The Red Men will measure the Blue Room to have a SMALLER LENGTH in the direction of motion than the Blue Man measures. In other words, the length of an object will shrink when it moves at high speed through an inertial reference frame.
So far, there are no good experimental tests of length contraction.
Why not?
However, we can look at a familiar situation to see how length contraction is at least consistent with the other phenomena we've examined so far. Remember the experiment in which Fred sent a proton flying through a tube in his lab?
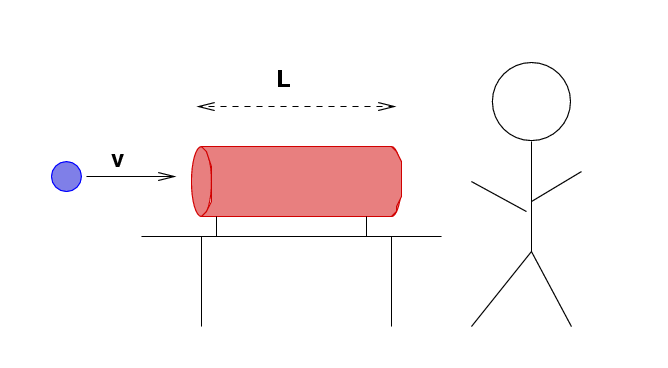
In this experiment,
Consider the events first from Fred's frame of reference in the lab.
Q: What is the space interval
between the two events?
Q: What is the time interval
between the two events?
Q: What is the space-time
interval between the two events?
Remember that we can also ask the proton about his measurements of these two events.
Q: What is the space-time
interval between the two events?
Q: What is the space interval
between the two events?
Q: What is the time interval
between the two events?
Now, suppose we were to ask the proton about the tube which briefly enclosed him. We might say, "Hey, Mr. Proton, did you notice the tube which just flew past you at v = 0.5 c? Can you tell us how long that tube was?"
Q: If Mr. Proton uses the time
interval between the two events,
and the speed of the tube, what
length will he derive for the tube?
Q: How does that length compare to
Fred's measurement of the tube's length?
Q: What is the "gamma" factor for
the tube as it flies past Mr. Proton?
You may recall that different observers may measure different intervals between two events, but that there is a maximum possible time interval:
An observer who is at rest and present at the location of two events will measure the shortest time interval between them; we call this the proper time interval.
In the same way, different observers may measure different lengths of an object. However, there is a maximum possible length:
An observer who is at rest relative to an object will measure it to have the longest size; we call this the proper length of the object.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.