 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
I want to show you a puzzle, but it will be easier to understand if we start with a simple scenario and work our way up to the puzzle; so, please be patient.
Alan stands out in the desert, next to a railroad track. There's a loose wire on the track. Every now and then, a spark jumps from the wire to the track.

The spark creates light rays that shoot off in all directions at the speed of light. As times passes, the light from the spark reaches greater and greater distances ....

Alan stands out in the desert, next to a railroad track. Beth stands on a railroad car next to Alan. The car sits motionless.
There's a loose wire on the track. Every now and then, a spark jumps from the wire to the track.
The spark creates light rays that shoot off in all directions at the speed of light. As times passes, the light from the spark reaches greater and greater distances ....
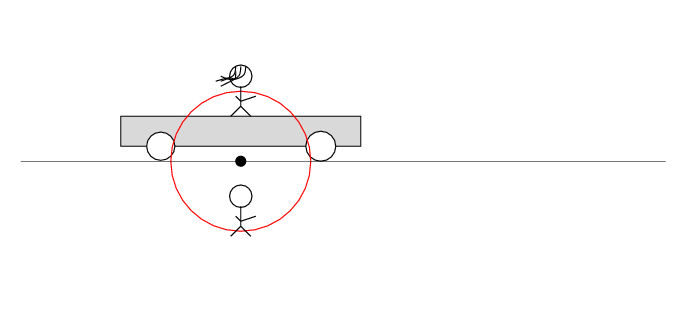
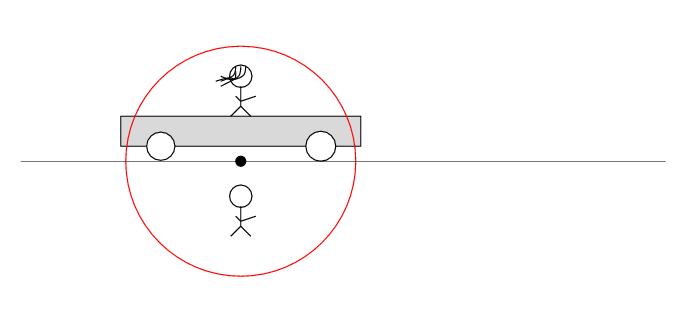
In Alan's frame of reference ...
Alan stands out in the desert, next to a railroad track. Beth stands on a railroad car nearby. The car rolls to the right at speed v.
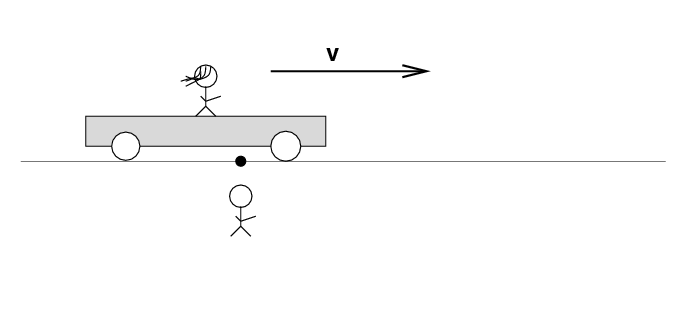
There's a loose wire on the track. Just as Beth passes Alan, a spark jumps from the wire to the track.
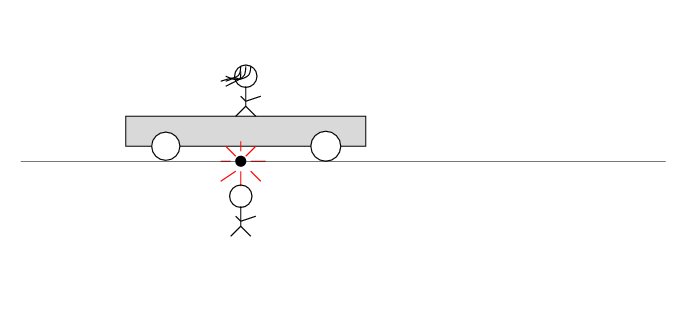
The spark creates light rays that shoot off in all directions at the speed of light. As times passes, the light from the spark reaches greater and greater distances ....
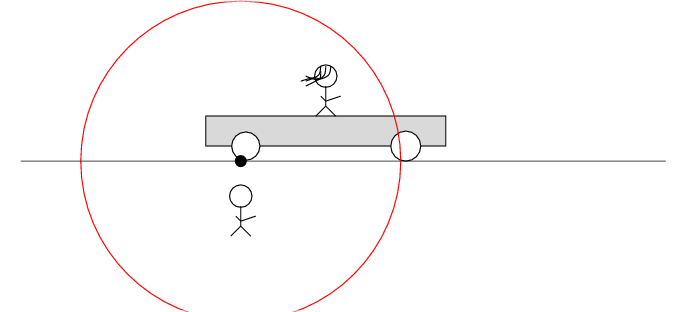
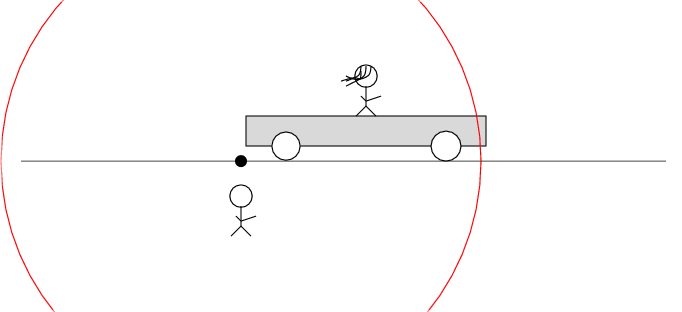
In Beth's frame of reference ...
Beth stands motionless on her railroad car. Alan and the desert move past her to the left at speed v. There's a loose wire on the track. Just as Alan passes Beth, a spark jumps from the wire to the track.
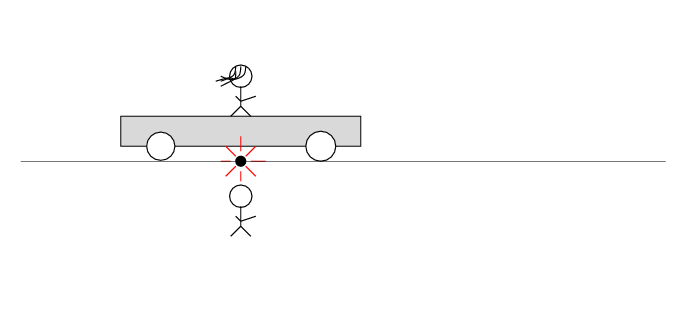
The spark creates light rays that shoot off in all directions at the speed of light. As times passes, the light from the spark reaches greater and greater distances ....
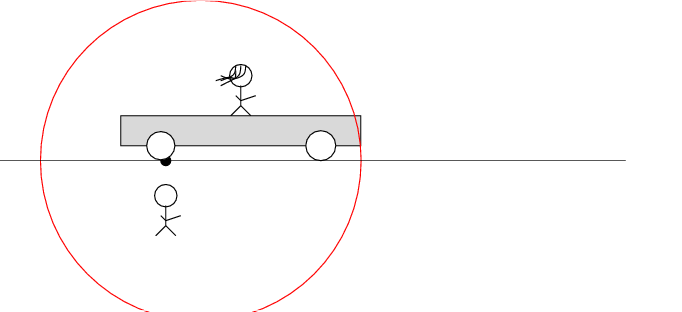
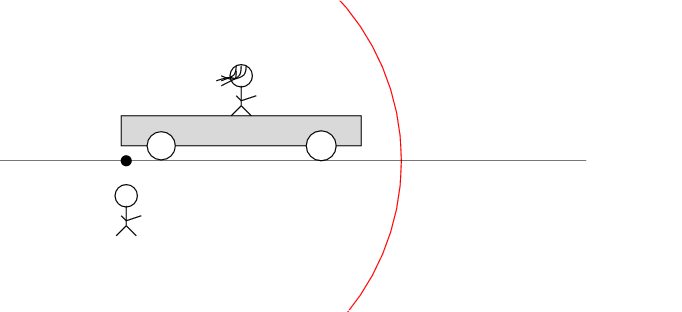
Okay, here comes the puzzle.
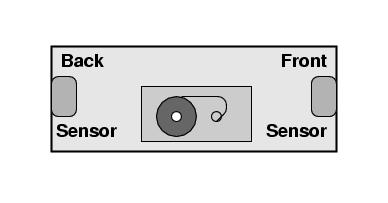
Beth brings her tape deck. Instead of an ON/OFF switch, it has two photosensors, one at each end of the unit. If a bright light strikes both sensors simultaneously, the tape deck will start playing. Beth has inserted a copy of Beethoven's Ninth Symphony into the tape deck.
In Alan's frame of reference ...
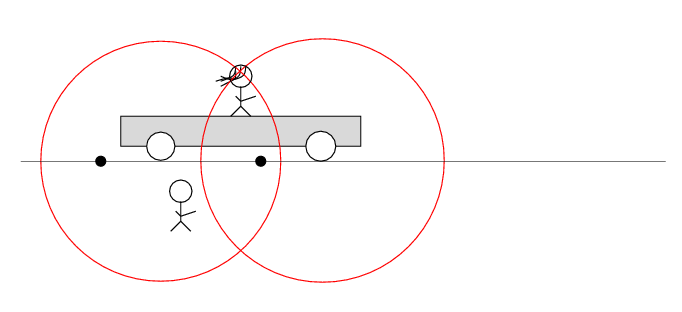
Alan stands out in the desert, next to the railroad track. Beth stands on a railroad car, with the tape deck at her feet on the car. The car rolls to the right at speed v.
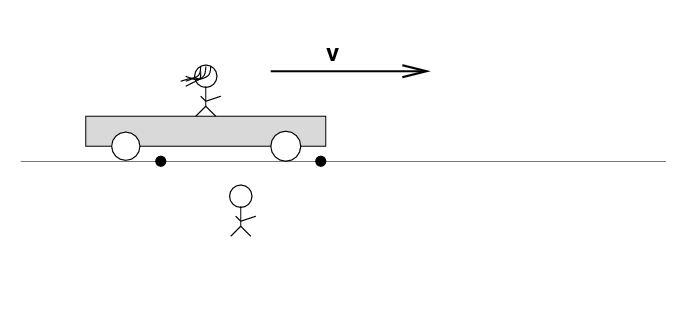
There are two loose wires on the track. Just as Beth passes Alan, a spark jumps from each wire to a wheel of the car.
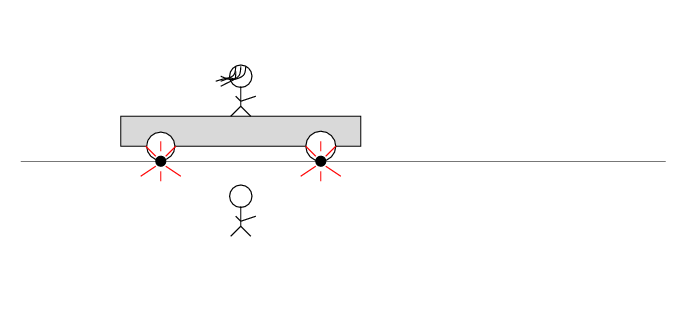
The spark creates light rays that shoot off in all directions at the speed of light. As times passes, the light from the spark reaches greater and greater distances ....
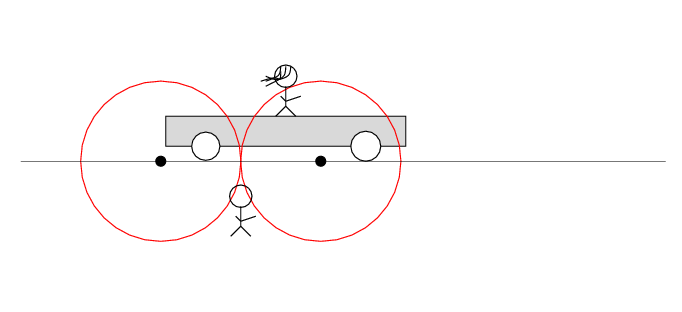
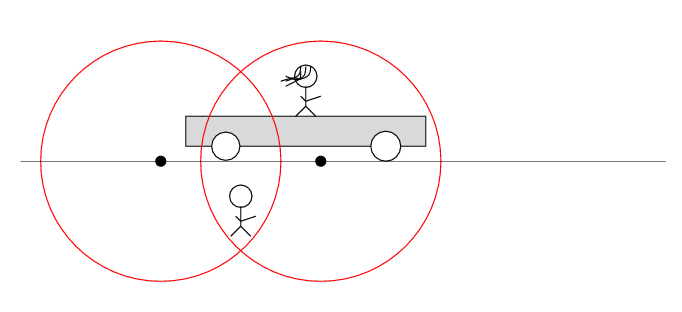
Q: Does the tape deck start to play?
In Beth's frame of reference ...
Beth stands on a railroad car with the tapedeck at her feet on the car. Alan stands out in the desert, next to a railroad track. Alan and the desert move past Beth to the left at speed v.
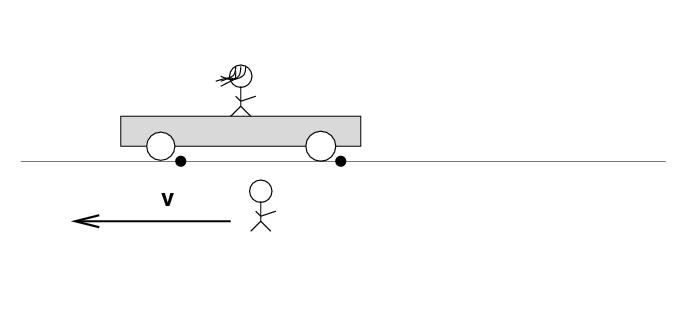
There are two loose wires on the track. Just as Alan passes Beth, a spark jumps from each wire to a wheel of the car.
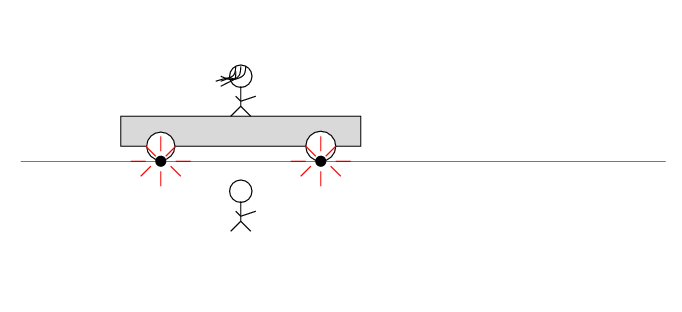
The spark creates light rays that shoot off in all directions at the speed of light. As times passes, the light from the spark reaches greater and greater distances ....
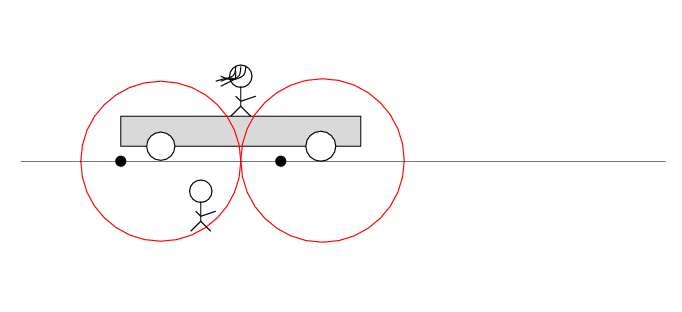
Q: Does the tape deck start to play?
The railroad car comes to a halt a short distance down the track. Beth grabs her tape deck and hops off the car onto the ground. She and Alan walk towards each other. They meet.
Q: Is the tape deck playing?
You have already seen a set of equations called "the Galilean transformations," which convert the coordinates and time measured by one observer to the coordinates and time measured by another. It turns out that these equations yield accurate results when observers are moving at speeds small compared to the speed of light ... but not for relativistic motion.
Today, we'll look at a different set of transformations, named for Dutch scientist Hendrik Lorentz. The Lorentz transformations work properly at relativistic speeds AND at the ordinary speeds of everyday life.
Once again, imagine two inertial frames of reference: Fred, standing on the ground, and Jane, flying past him at high speed.
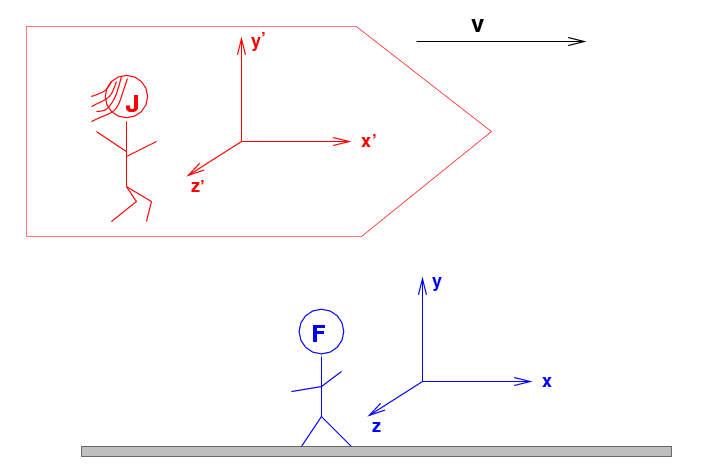
We'll denote Fred's measurements (and those of his assistants) with the regular symbols:

while Jane's measurements (and those of her assistants) will be written with "prime" markers:
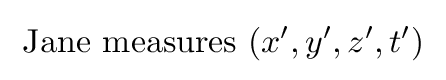
Jane's spaceship flies past Fred at a speed of v in the positive x-direction, to the right.
I will not derive the Lorentz transformations here. If you wish, you can read the derivation in Taylor and Wheeler, or in Professor Lindberg's notes (see pages 40-42 in particular). The bottom line is that if Jane moves in the x-direction relative to Fred with velocity v, then we can convert Fred's measurements to Jane's measurements like so:
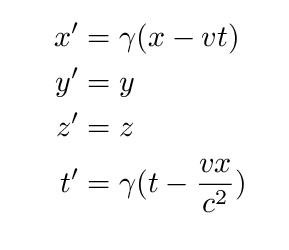
If you happen to be writing velocities in terms of the speed of light, so that someone moving at half the speed of light is given a velocity v = 0.5, and a beam of light is given a velocity v = 1, then the final equation simplifies to

Note the BIG difference between this set of equations and the Galilean transformations: here, not only does the position of an event depend on the observer, but the time of an event depends on the observer, too. The measurements of both space and time in the moving reference frame depend on both the space and time coordinates of the event in the stationary frame (and vice versa). It looks like we can no longer separate space from time; instead, events are immersed in a 4-dimensional matrix of space-time.
This mixture of space and time reminds me of another situation in which two distinct entities became inextricably combined, with a happy result:Hey, you got chocolate in my peanut butter!
You got peanut butter in my chocolate!
Maybe this will make some sense if we apply the Lorentz transformations. Let's put some nice, round numbers into the situation, too. For simplicity, let's use units of meters (m) to measure both space and time. The speed of light is simply v = (1 m of space) / (1 m of time) = 1.
Alan's coordinate system is centered on him, so he stands at x = 0 m. Alan and his assistants measure the position of the two loose wires to be x1 = -10 m and x2 = 10 m. He and his assistants measure the time at which the sparks occur. They determine that the sparks are simultaneous, both occuring at time zero. So t1 = 0 m and t2 = 0 m.
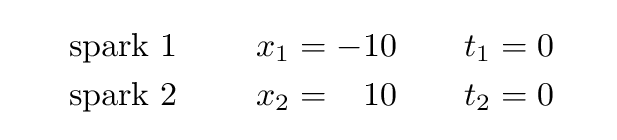
Beth and her assistants roll past Fred at a speed of v = 0.5c. They decide that the moment when Alan passes Beth will be t' = 0 m, and they measure all distances relative to Beth, so she stands at x' = 0 m. Can you figure out the space and time coordinates for these two events, according to Jane and her team?
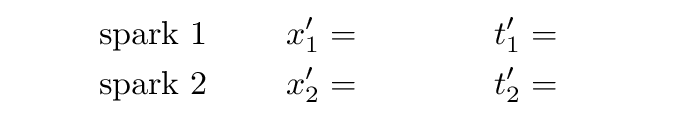
You should discover one of the fundamental aspects of special relativity: events which are simultaneous in one reference frame may not be simultaneous in a different reference frame.
So, here's the sequence of events from Alan's point of view, in which the sparks occur simultaneously. Note that the light waves from the right-hand spark reach Beth and her tape recorder before the light waves from the left-hand spark. Alan concludes the tape recorder does not play.
And here are the same events as measured by Beth and her assistants. Note that
Beth also concludes the tape recorder does not play.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.