
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Astronomers have known for some time that a small fraction of galaxies have peculiar "jets" extending from their very centers. For example, if you look near the center of the Virgo Cluster of galaxies (the nearest big cluster to our own Milky Way)
you'll see a big elliptical galaxy. Astronomers call it "M87" because it was the 87'th object noted in a list of fuzzy blobs which were NOT comets, made by the French comet hunter Charles Messier. This looks looks like an ordinary elliptical galaxy in a long exposure photograph:

But this short exposure, which shows only the brighest regions near the very center of the galaxy, reveals a jet:


These pictures are scans of photographs printed in
The Hubble Atlas of Galaxies.
The one showing the jet was taken Mar 8/9, 1934,
with the 100-inch telescope at Mt. Wilson.
Jets, by themselves, are peculiar: why should matter and/or energy be ejected from the center of a galaxy? Why should it be squirted in such a narrow beam? But some of them become even more peculiar if you look at them over a period of time, using telescopes which can perceive very fine details.
This, for example, is a recent HST image of the jet in M87. Note that the jet is broken into knots:

Let's rotate our view for convenience so that the jet points to the right:

If you zoom in on an inner portion of the jet, you can see little blobs which appear to shoot out to the right over just a few years:
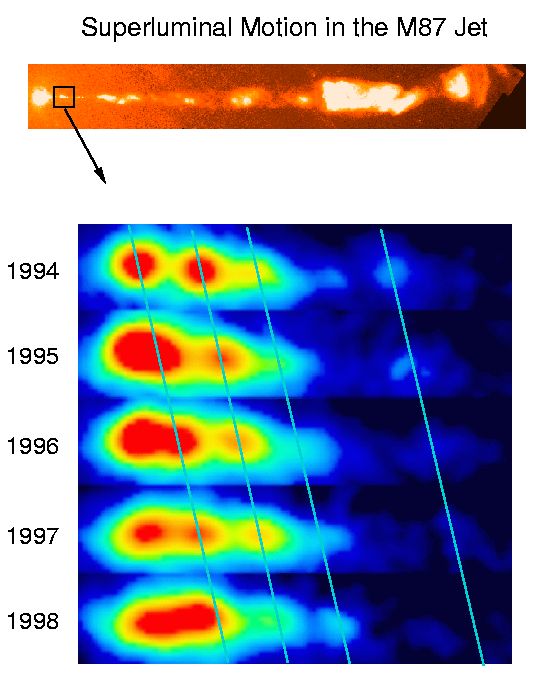
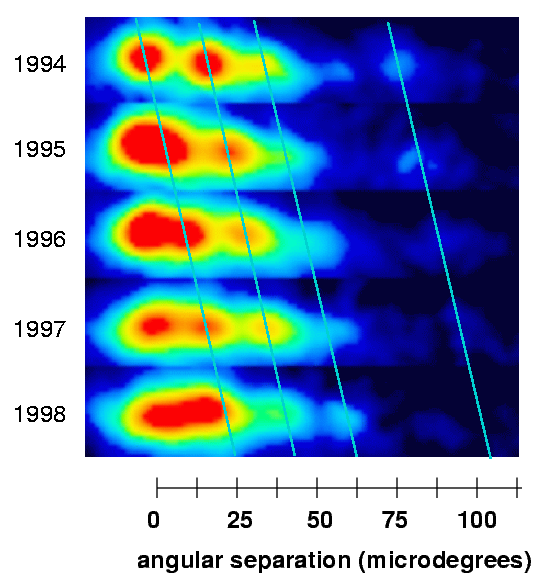
Now, we can measure the angular separation between the center of the galaxy and individual knots. The figure below has a scale to help you estimate the angular velocity of the blobs.
The distance to this galaxy, M87, is about D = 62 million light years. One can use this distance to convert angular separations into linear separations across the line of sight. I've done that in the version shown below.
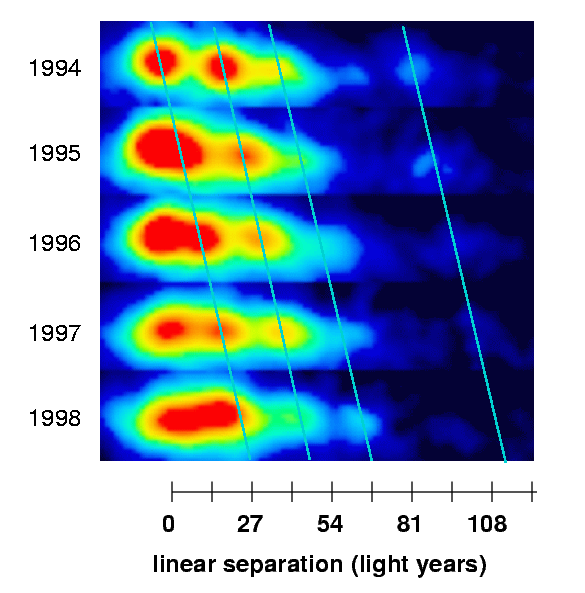
Now, look carefully at one of the blobs: the innermost one, which appears most clearly in 1996 and 1997.
Q: How far did this blob of material appear to move?
How long did it take to move that distance?
What was the blob's apparent speed?
But ... but .... but .... Einstein said "No material object can move (through a vacuum) faster than the speed of light (in a vacuum)." How can this be?!
Here's another way of looking at the M87 jet: a movie made from 11 radio observations spaced at 3-week intervals. Craig Walker created this movie from a series of observations with the VLA. Each tick mark represents about 0.25 light-years at this scale.
Finally, here's one more graph showing the motion of blobs in M87's jet over the course of about 4 years.
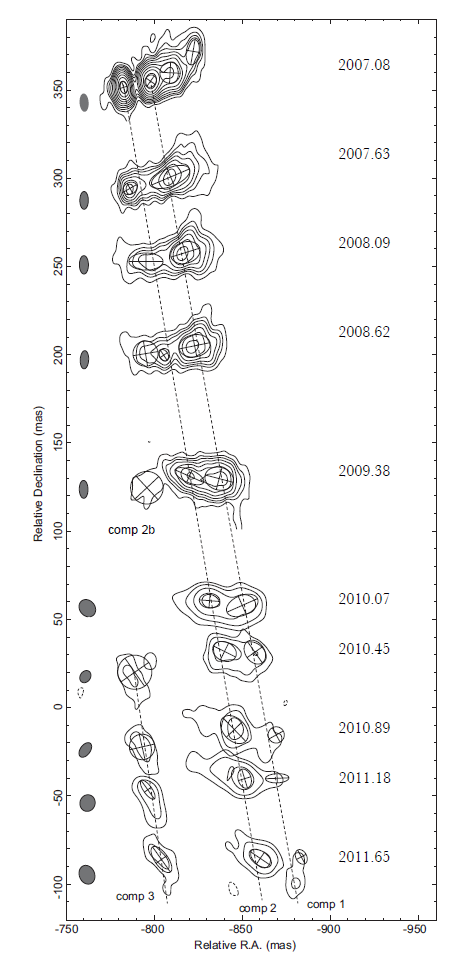
Figure 1 from
Casadio et al., "A sensitive study of the peculiar jet structure HST-1 in M87"
Let's back up a bit and look at what might be happening. First of all, just because the jet shoots out to the right of the nucleus doesn't necessarily mean that the jet is in fact pointing straight to the right; it might have a component pointing towards us or away from us. Let's see what happens if a jet of material happens to be shooting both towards us and to the right. For convenience, I'll pick a source which is exactly 100 light years away from the Earth.
If we float far above the jet and look down, we would see the blob move like this over a period of three years.
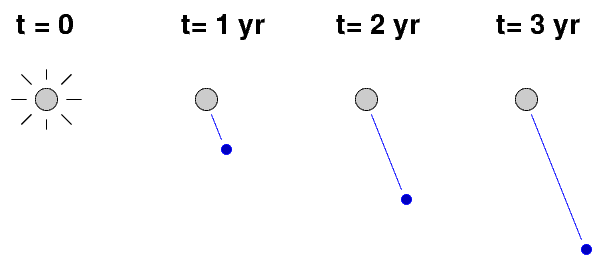
Let's zoom out to see the Earth, too, from our vantage point far above the galaxy:
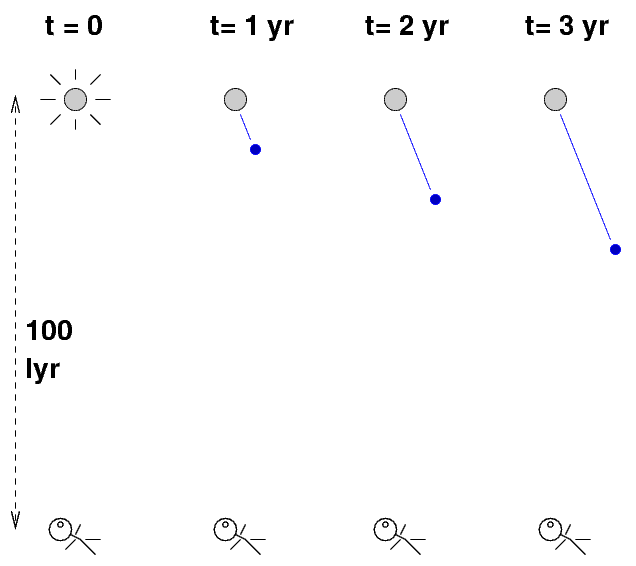
The question is -- what do we see from our vantage point on Earth, and when do we see it?
We can break up the motion of the blob into two components:
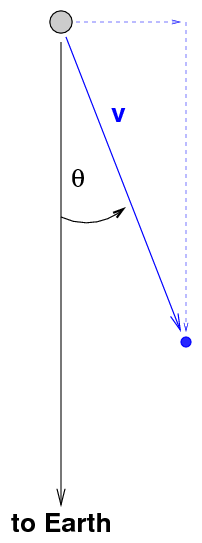
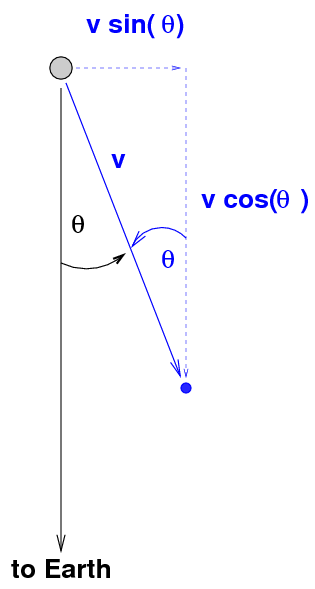
Okay, now go back to the diagram showing the motion of the jet and the observer on Earth:
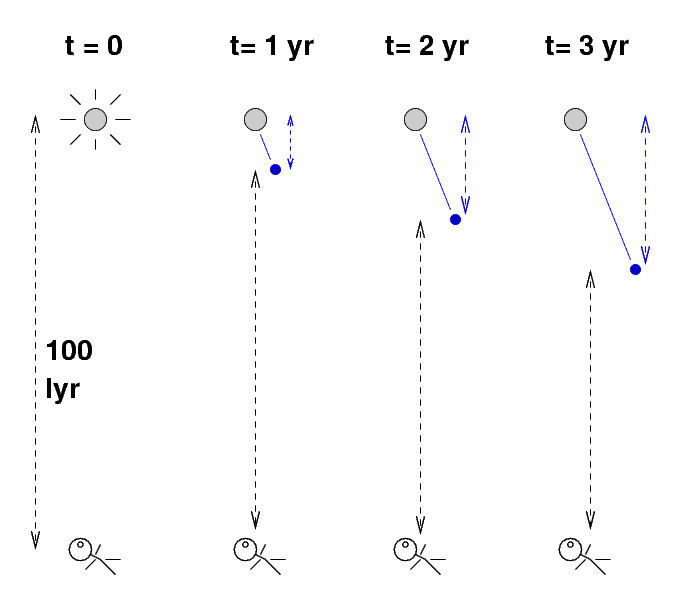
Remember, according to Special Relativity, the speed of a light ray is always the same, even if it is emitted from a rapidly moving object.
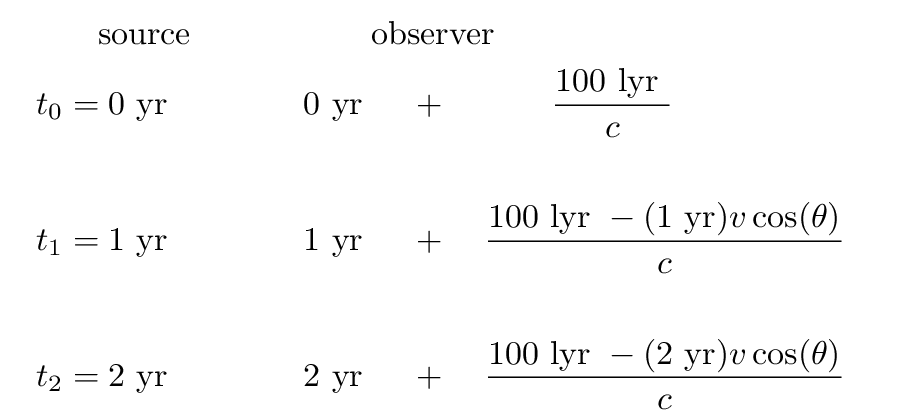
If the observer measures the interval between the moment the nucleus flares up (t0) and the moment the blob is at the first position shown in the figure (t1), he will find
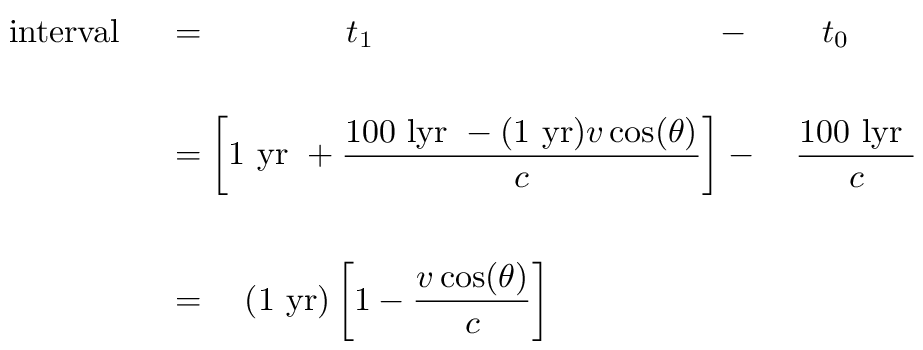
During this interval, the blob appears to move a transverse distance
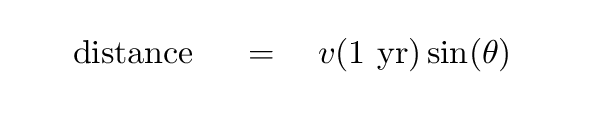
So, the blob appears to move across the line of sight (transversely) with a speed of

Hmmmm. We have sin(theta) on the top and cos(theta) on the bottom. This could be complicated. Let's make a graph of these functions to see how they behave.
For the relatively slow speed of v = 0.1 c , we see that the cosine term is just a little bit smaller than 1.0.
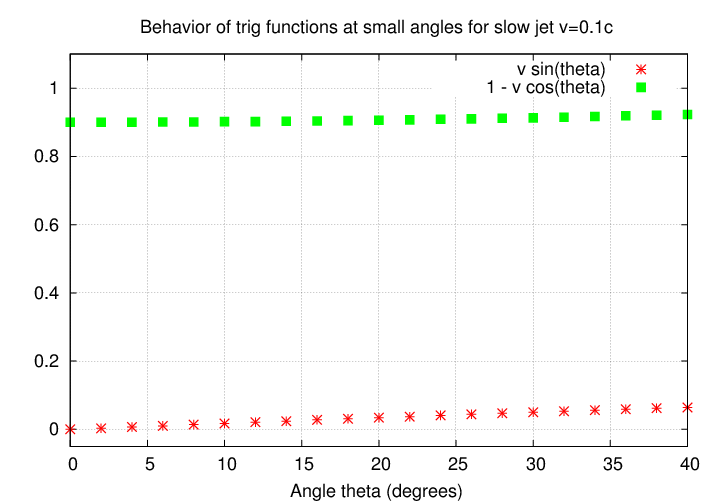
That means that when we calculate
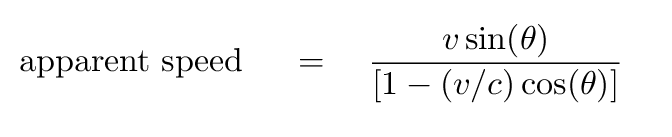
we will boost the real speed by a very small factor, and it will still appear small compared to c.
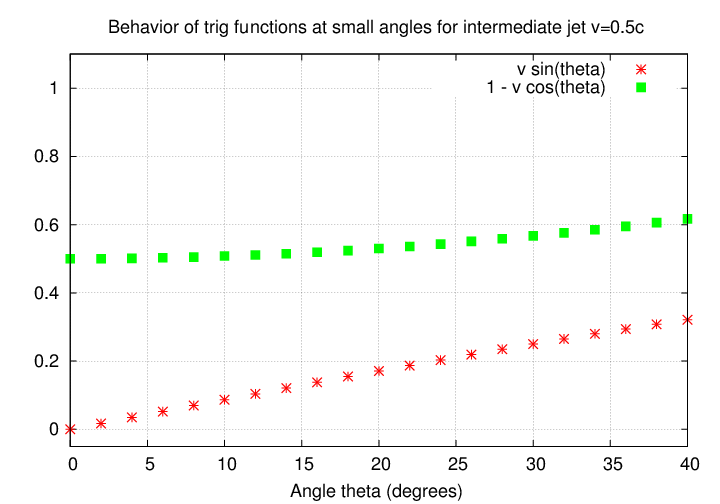
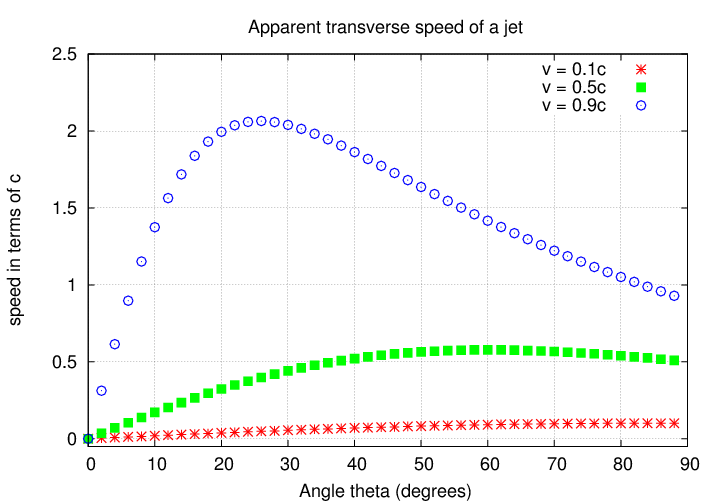
But as the jet speed increases, the term on the bottom becomes larger. That means that the apparent transverse speed is boosted by a larger and larger amount. For v = 0.5 c , for example,
For v = 0.9 c
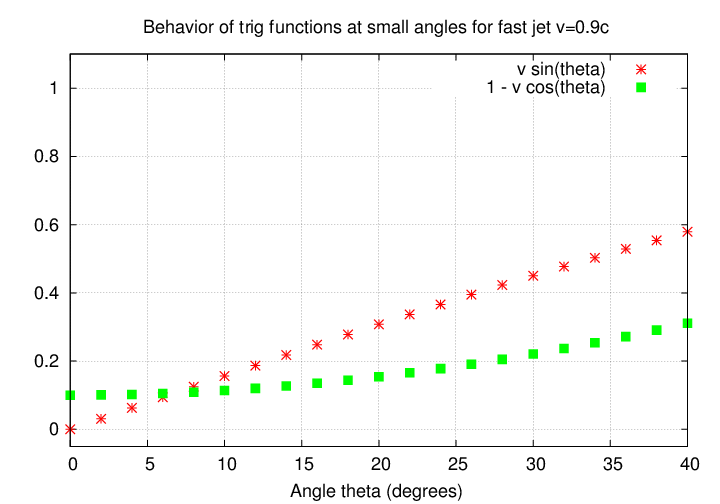
For v = 0.99 c , the (1 - cosine) term is now almost zero, which means we are dividing by a very small number.
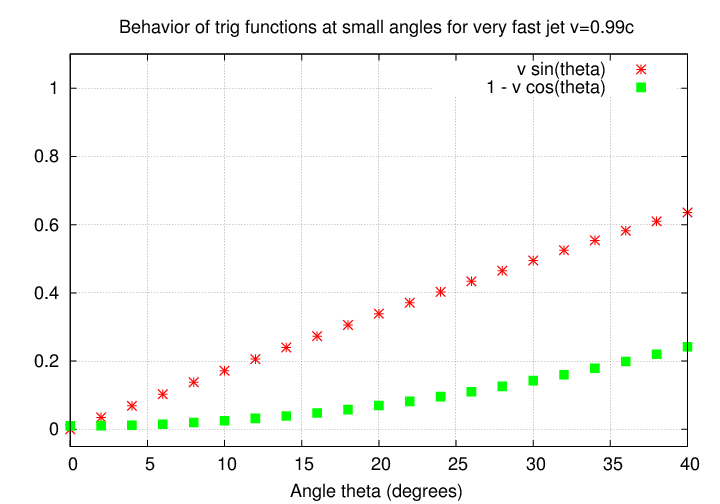
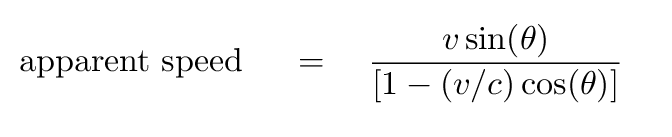
Q: Can you calculate the apparent transverse
velocity of material in a jet for
several angles? Fill in this table
angle θ = (degrees)
5 10 15 20
========================================================================
V = 0.1c
v sin(θ)
1 - (v/c)cos(θ)
apparent speed
-----------------------------------------------------------------------
V = 0.5c
v sin(θ)
1 - (v/c)cos(θ)
apparent speed
-----------------------------------------------------------------------
V = 0.9c
v sin(θ)
1 - (v/c)cos(θ)
apparent speed
========================================================================
The result of all this is that the apparent transverse speed can be larger than c for certain combinations of true jet speed and angle.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.