
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Because special relativity deals with events which are outside the boundaries of our everyday experience, it leads to some predictions which go against our common sense. That's not a bad thing -- it's just due to our lack of experience. If we were able to run at 0.5c, our "common sense" would be in perfect agreement with these predictions.
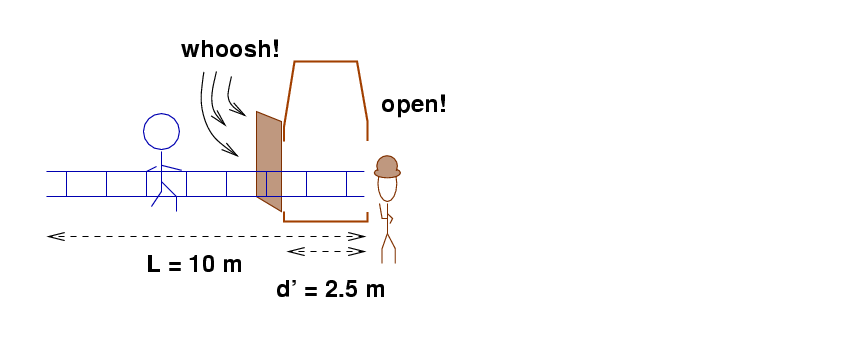
Let's look at one of the most common "paradoxes" used in discussions of special relativity. My version involves a ladder and a barn, but you may also see a version with a train and a tunnel.
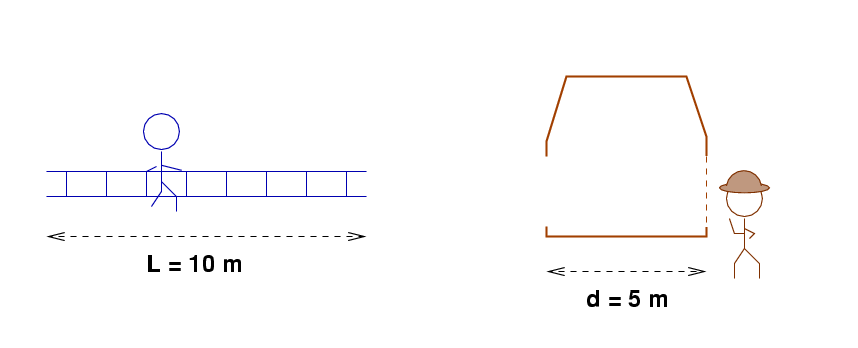
Fred has ladder. The ladder is L = 10 m long when Fred measures it.

Farmer Brown has a barn. The barn is d = 5 m wide. The front door (on the left side) is open, but the back door (on the right side) is currently closed.
It starts to rain. "Oh, no!" wails Fred, "My beautiful ladder will become wet! Wait ... over there, I see a barn. I can run over there and take my ladder into the barn. Then it will stay nice and dry!"
Fred starts to run towards the barn at v = 0.866c.
As Fred runs towards the barn, his ladder contracts in the direction of motion. In fact, it contracts by a factor of
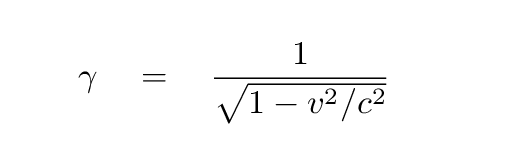
Q: What is the length of the ladder
in the frame of Farmer Brown?
So, it looks like the ladder will fit into the barn.

However, just as the back end of the ladder enters the barn, a gust of wind blows the front door shut. Fortunately, at the same moment, Farmer Brown opens the back door.
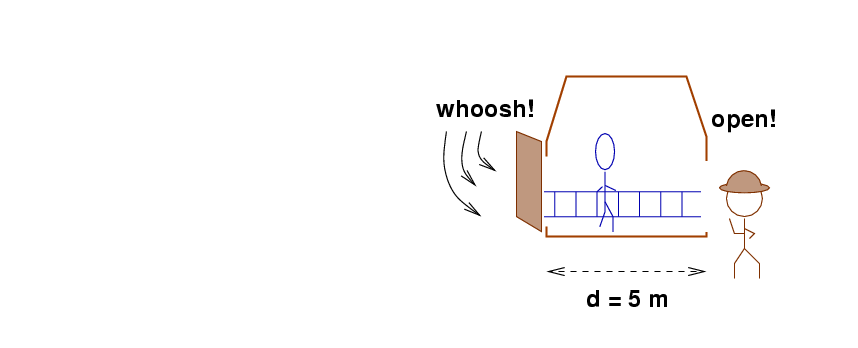
The result is not so bad: there's no damage to the ladder or the barn, but the ladder will go out into the rain again.
As the barn moves towards Fred, it contracts in the direction of motion. In fact, it contracts by a factor of
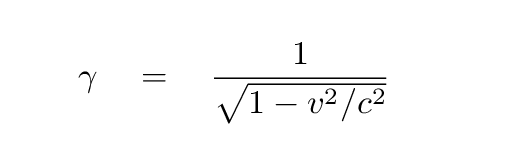

This doesn't look good. Fortunately, as the right end of the ladder is just about to strike the back door, Farmer Brown opens the back door. Phew. Just at this same moment, however, a gust of wind blows the front door closed.
Disaster! The door crashes into the ladder, breaking it into pieces. Fred is heartbroken.
Q: Which is it?
a) the ladder is unhurt, just wet
b) the ladder is broken into pieces
Only one of these possibilities can
be what actually happens -- it is not
possible for the ladder to be BOTH
broken and intact.
In order to figure out what really happens, it will help to have some extra observers scattered throughout space. Fred's assistants move together with Fred. Each has synchronized his clock with Fred's, and each has his own meterstick and notebook. Farmer Brown's assistants, likewise, have synchronized their clocks with Farmer Brown, and have their own metersticks and notebooks.
As events occur, the observers who are present will note the time and location of each one. They decide to use the convention:
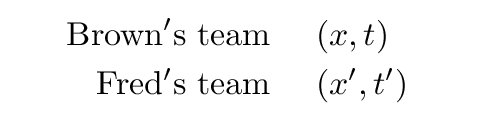
In Farmer Brown's reference frame ....
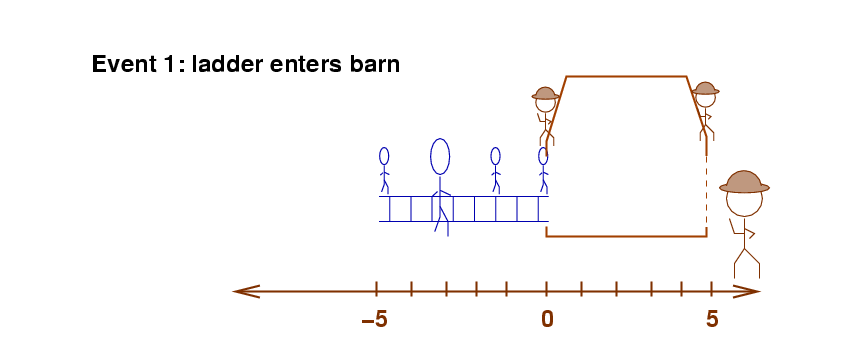
The first event occurs when the front of the ladder enters the left-hand door of the barn.
Q: Which observer in Farmer Brown's frame
of reference measures the time and
location of this event?
That observer determines that this
event takes place at time t = 0 meters.
What is the location of this event?
Now, Fred and the ladder continue to zoom to the right at v = 0.866c. Event number 2 occurs when the front of the ladder reaches the right-hand side of the barn.

Q: Which observer in Farmer Brown's frame
of reference measures the time and
location of this event?
What is the location of this event?
What is the time of this event?
Event number 3 occurs when the back of the ladder reaches the left-hand side of the barn.

Q: Which observer in Farmer Brown's frame
of reference measures the time and
location of this event?
What is the location of this event?
What is the time of this event?
Let's summarize the measurements made by Farmer Brown and his assistants.
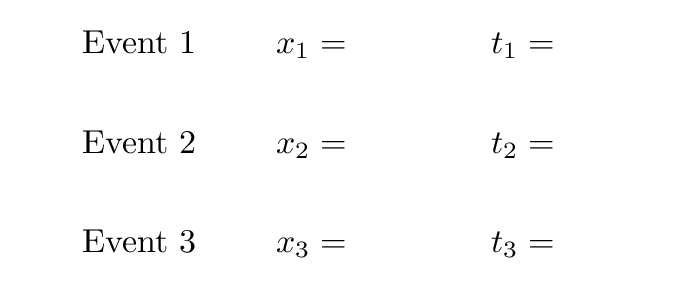
In Fred's reference frame ....
The first event occurs when the front of the ladder enters the left-hand door of the barn. For convenience, we'll arrange things so that the origin of both coordinate systems, meet at this moment ... and so that the clocks of the observers at this location agree at this moment, too.
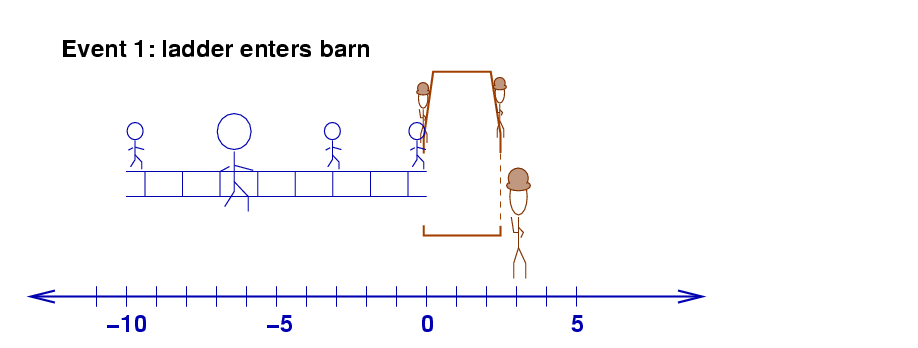
Q: Which observer in Fred's frame
of reference measures the time and
location of this event?
That observer determines that this
event takes place at time t' = 0 meters.
What is the location of this event?
Now, your job is to use the Lorentz transformations to convert all of the measurements made by Farmer Brown and his assistants into the corresponding values measured by Fred and his assistants.
Q: Draw a picture showing the locations of
Fred, the ladder, Farmer Brown, and the
barn, at the moment of Event 2,
according to the measurements in
Fred's reference frame.
Q: Draw a picture showing the locations of
Fred, the ladder, Farmer Brown, and the
barn, at the moment of Event 3,
according to the measurements in
Fred's reference frame.
You can check your results against mine:
Q: Does the ladder break into pieces,
or does it remain whole? Explain.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.