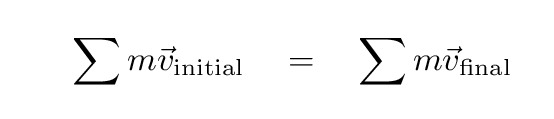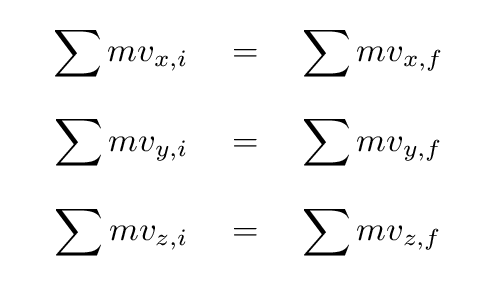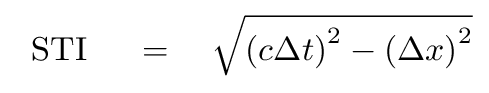Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Momentum in the low-speed regime
You have probably discussed momentum
in an earlier physics course.
Momentum is a combination of the mass of a body
and its velocity,
just like kinetic energy.
There are two main differences between
KE and momentum, however.
- Momentum is a vector quantity, whereas KE is a scalar.
The momentum of a body has a direction as well as a size;
the direction is just the direction of motion.
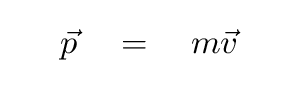
That means that there are really three quantities
involved in the calculation of momentum, not just one.
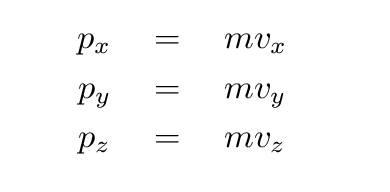
- The units are different: momentum involves the velocity of the
object raised to the first power, whereas KE involves
the square of the velocity. That means that the
standard SI units for momentum must not be Joules.
In fact, the units for momentum don't have a fancy
name ....
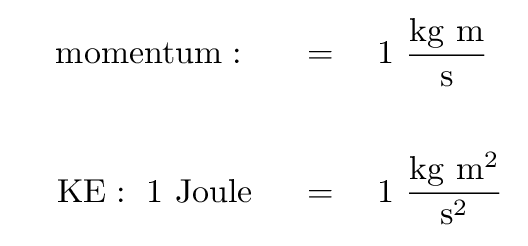
If, for some reason, we wanted to convert a momentum-like
quantity into an energy-like quantity, we would have
to multiply by a velocity-like quantity:
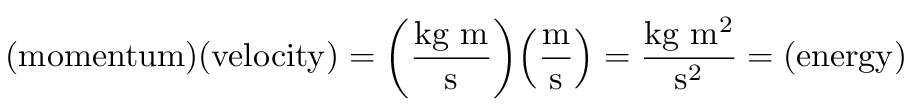
Let's do a few simple examples.
Q: I toss a rubber ball of mass m = 0.2 kg
gently to the East at v = 5 m/s.
What is the ball's momentum?
Q: Crazy Ellie fires a 125-grain cartridge from
her Smith and Wesson .357 Magnum handgun
(one grain is approx 0.065 grams).
The bullet leaves the muzzle of the
gun at v = 440 m/s towards the East.
What is the bullet's momentum?
Note that the momentum of a single bullet fired by a handgun
isn't really much larger than that of an ordinary ball,
tossed gently.
That may surprise you,
if you've seen
too many Hollywood movies.
What good is momentum?
Why bother with momentum?
One of the main reasons is that when objects
collide or interact,
then -- as long as there are no significant external forces --
the initial momentum of the system is the same as the final momentum.
Be careful: this applies to the sum over all the objects
involved, not each object individually. In other words,
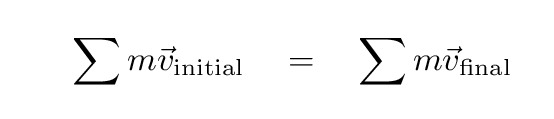
In fact, this equality must apply to each component of the
vector momentum, so we could also write an equation for
each component separately.
I'll use subscripts i to mean "initial" and
f to mean "final".
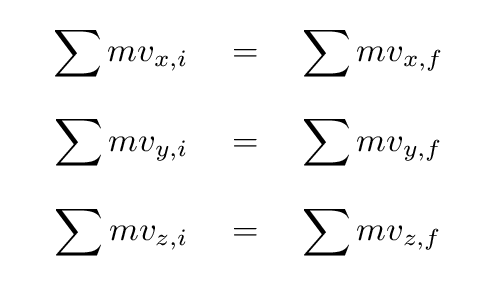
You may recall that
when I discussed kinetic energy,
I was careful to add lots of qualifiers to the
statement
"kinetic energy is SOMETIMES conserved in interactions
between particles."
It was only collisions between hard, compact balls --
the "elastic" collisions -- in which KE was conserved.
For example, in this collision between two cars
(click on the first picture for a very large movie),
KE is definitely NOT conserved:
- both cars are motionless afterwards, so the final KE is zero
- a great deal of KE was dissipated in the process
of deforming pieces of metal, breaking glass, and so forth


MPEG = MPEG v1 version
AVI = MPEG-4 version
MOV = Apple Quicktime
On the other hand, the total momentum of this pair of
cars IS conserved:
- the initial momentum was zero in each direction -- why?
- the final momentum is zero in each direction
Let's work through a few simple examples of momentum
in the non-relativistic regime,
just to see how it can be used in practice.
Car slams into truck and sticks to it
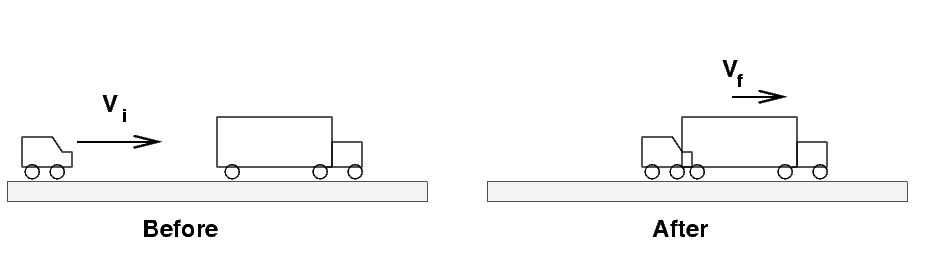
A car of mass m1 = 2000 kg
moving at vi = 20 m/s
slams into a stationary truck of mass
m2 = 15,000 kg.
Immediately after they collide,
what is the speed with which the combined
wreckage slides forward?
Which of the following is the final velocity vf?
- 20.0 m/s to the right
- 4.21 m/s to the right
- 2.67 m/s to the right
- 2.35 m/s to the right
Car rolls into truck and bounces off gently
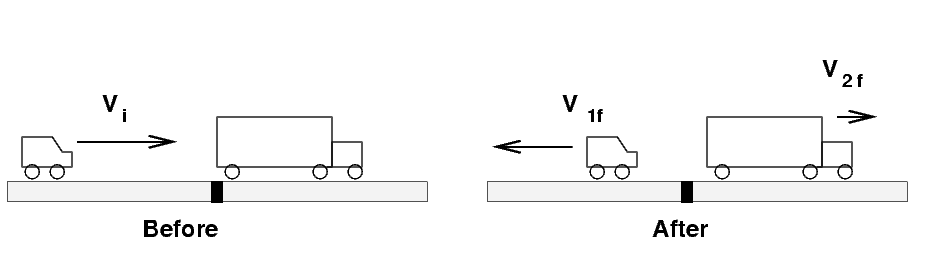
A car of mass m1 = 2000 kg
rolling slowly at vi = 5 m/s
bumps into a stationary truck of mass
m2 = 15,000 kg.
Afterwards, the car
moves backwards
with velocity
v1f,
and the truck creeps forward at
v2f.
Which of the following are closest to the final velocities?
- car 5.0 m/s to the left, truck 1.53 m/s to the right
- car 2.0 m/s to the left, truck 0.93 m/s to the right
- car 1.0 m/s to the left, truck 0.53 m/s to the right
Car and minivan smash into each other
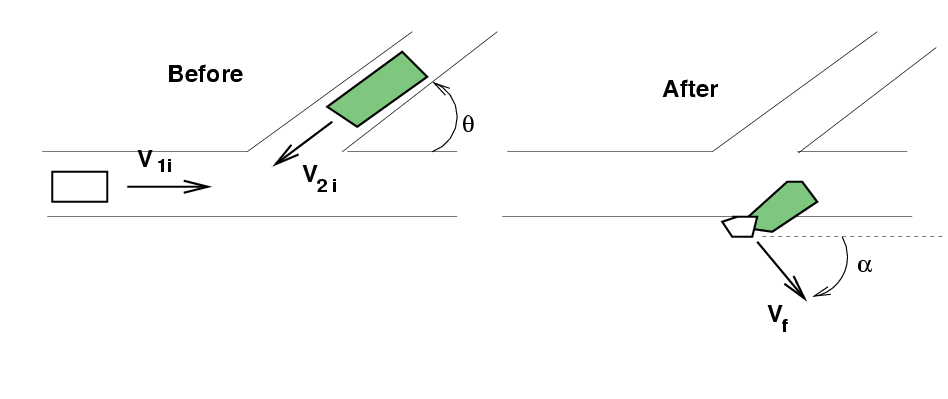
A car of mass m1 = 2000 kg
is driving at
v1i = 20 m/s due East
as it enters an intersection.
A minivan of mass
m2 = 6000 kg
going
v2i = 30 m/s
drives into the intersection along a road
which runs θ = 30 degrees
South of West.
The meet in a most unhappy fashion.
Which of the following is the final velocity of the
combined wreckage?
- (-19.3 m/s East, -12.5 m/s North)
- (-14.5 m/s East, -11.3 m/s North)
- (-11.3 m/s East, -15.3 m/s North)
If the angle α is drawn as shown,
how large is it?
- about 38 degrees
- about 128 degrees
- about 142 degrees
Is momentum an invariant quantity?
An invariant quantity is one that
has the same value, no matter which observer is making measurements.
The space-time interval
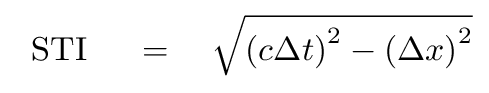
is an example of an invariant quantity.
Is kinetic energy an invariant quantity?
Let's find out.
The Blue Man throws a ball (m = 0.2 kg )
at a speed of v = 20 m/s to the right.
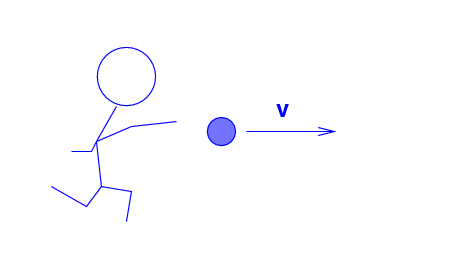
Q: What is the momentum of the ball,
according to the Blue Man?
But the Blue Man and the ball are all travelling across
the landscape at a speed of w = 50 m/s to the right,
as measured by the Red Men.
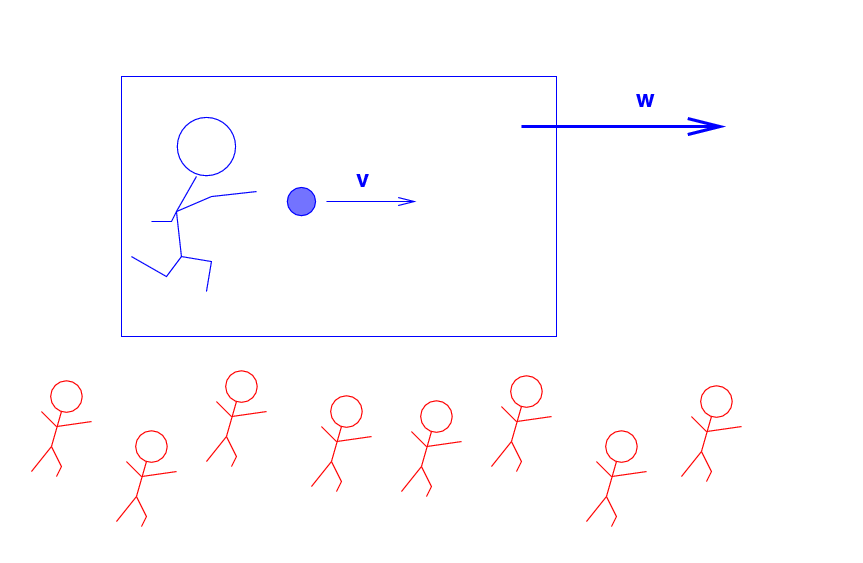
Q: What is the momentum of the ball,
as measured by the Red Men?
For more information
- You might look at the notes to one of the other courses I teach,
University Physics I
for more details about kinetic energy and momentum
in the non-relativistic regime.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
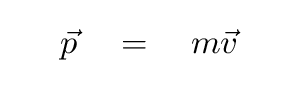
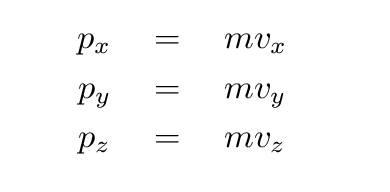
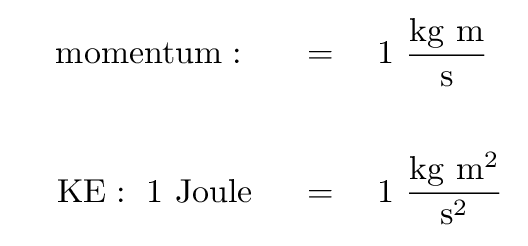
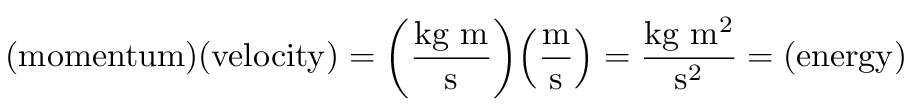
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.