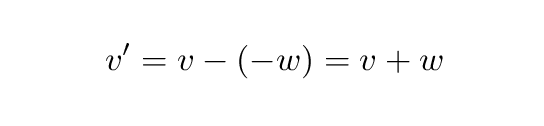
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Let's work through a few situations to see just how the Lorentz transformations take us to worlds that may be, well, a bit counter-intuitive.
Fred measures a bird to fly past him at velocity v (in other words, to the right). Jane and her assistants zoom past Fred with velocity -w (in other words, to the left). So, to be clear,
In the Galilean world, adding velocities is really easy. Jane's measurements will indicate that the bird is moving at speed
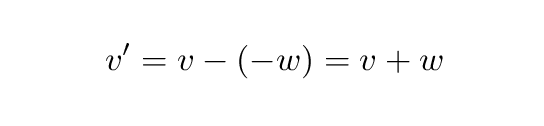
How do we know that velocities add like this? Well, we could work out the velocity of the bird explicitly by figuring out its location at two different times. For example, Fred measures the position of the bird when it goes TWEET, and when it meets the dog:
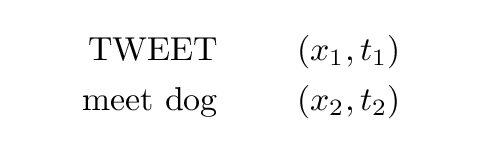
Using the Galilean transformations, we can figure out the locations and times of these two events in Jane's reference frame:
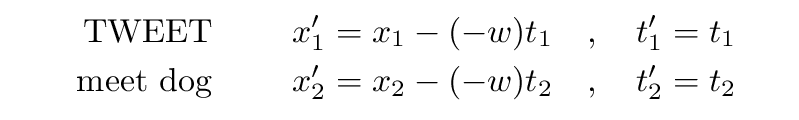
Jane calculates the speed of the bird in her reference frame in the usual manner: she divides its displacement in position by the time it took to move.
We can follow exactly the same procedure under the Lorentz transformations to find the speed of the bird, based on Jane's measurements.
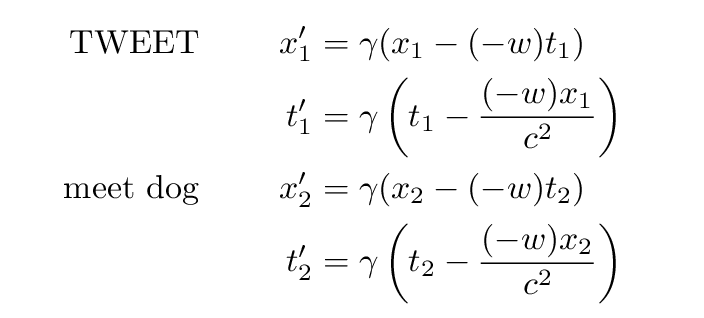
Once again, Jane calculates the speed of the bird by dividing its change in position by the time interval.
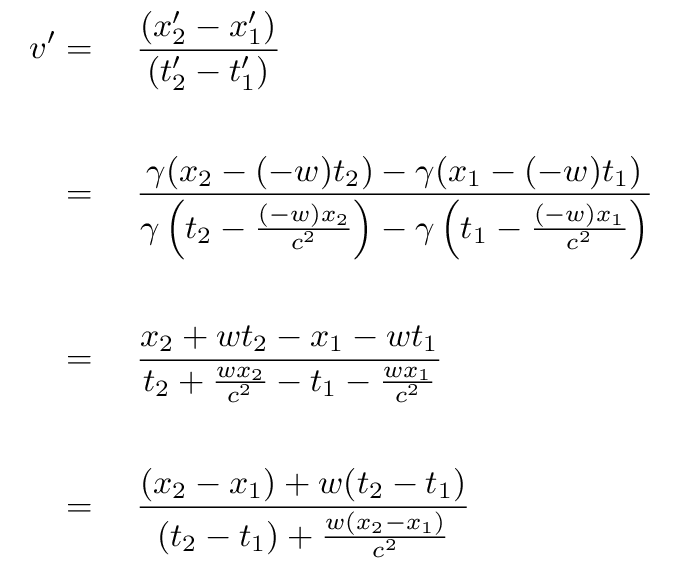
Q: Can you simplify this expression for the
speed of the bird, according to Jane?
Hint: divide the top and the bottom
by the quantity (t2 - t1).
You should be able to derive the simple formula
Q: In the example problem, the bird flew
at v = 0.9c according to Fred,
and Jane zoomed past Fred at w = -0.3c.
What was the speed of the bird v' according
to Jane?
Q: What if v = 0.9c and w = -0.9c?
Q: Suppose that the Fred measures the progress
of a laser light beam instead of a bird.
He determines the beam travels at v = 1c.
If Jane is moving at w = -0.9c relative
to Fred, what will she measure for the speed
of the light beam?
In the general case that Fred determines an object to move at speed v, and Jane's reference frame translates past Fred with velocity w, the Lorentz transformations imply that Jane will measure the object to move at
Q: Fred stands still. He tosses a ball
to the left at 0.3c. Meanwhile, Jane
drives her car past Fred to the left
at 0.6c.
What is the speed of the ball in
Jane's frame of reference?
Q: Fred stands still. Jane drives her
car past Fred to the left at 0.6c.
She tosses a ball forward at a speed
of 0.3c.
What is the speed of the ball in Fred's
frame of reference?
I want to show you a puzzle, but it will be easier to understand if we start with a simple scenario and work our way up to the puzzle, so, please be patient.
Alan stands out in the desert, next to a railroad track. There's a loose wire on the track. Every now and then, a spark jumps from the wire to the track.
The spark creates light rays that shoot off in all directions at the speed of light. As times passes, the light from the spark reaches greater and greater distances ....
Alan stands out in the desert, next to a railroad track. Beth stands on a railroad car next to Alan. The car sits motionless.
There's a loose wire on the track. Every now and then, a spark jumps from the wire to the track.
The spark creates light rays that shoot off in all directions at the speed of light. As times passes, the light from the spark reaches greater and greater distances ....
In Alan's frame of reference ...
Alan stands out in the desert, next to a railroad track. Beth stands on a railroad car nearby. The car rolls to the right at speed v.
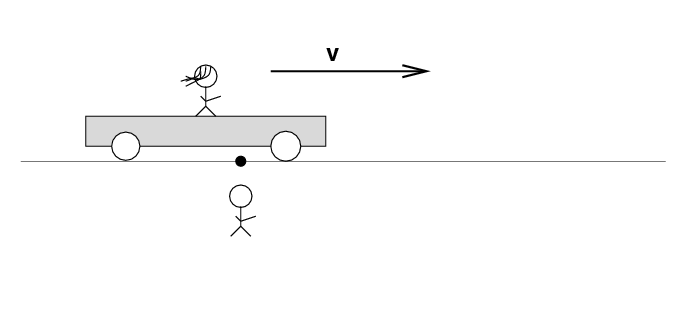
There's a loose wire on the track. Just as Beth passes Alan, a spark jumps from the wire to the track.
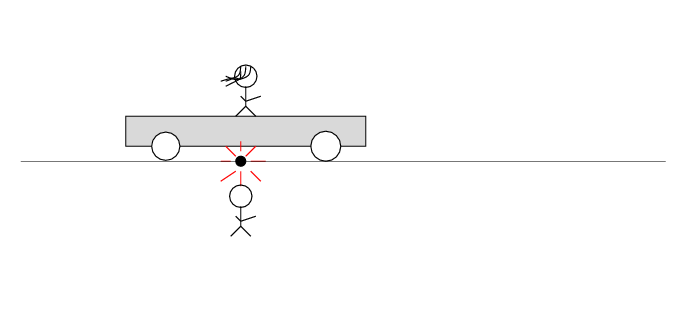
The spark creates light rays that shoot off in all directions at the speed of light. As times passes, the light from the spark reaches greater and greater distances ....
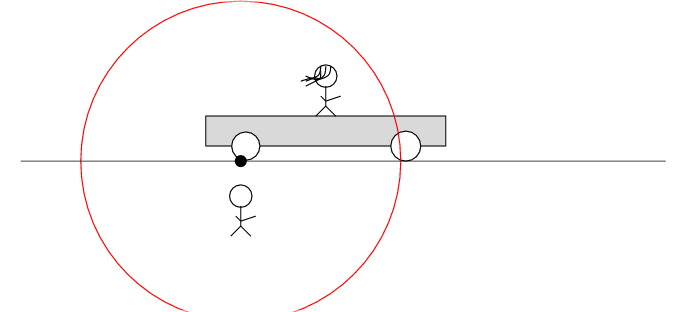
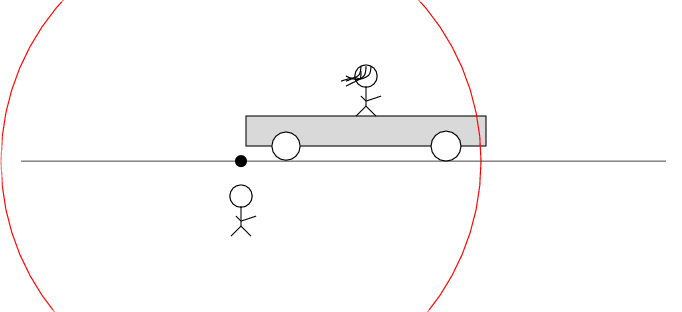
In Beth's frame of reference ...
Beth stands motionless on her railroad car. Alan and the desert move past her to the left at speed v. There's a loose wire on the track. Just as Alan passes Beth, a spark jumps from the wire to the track.
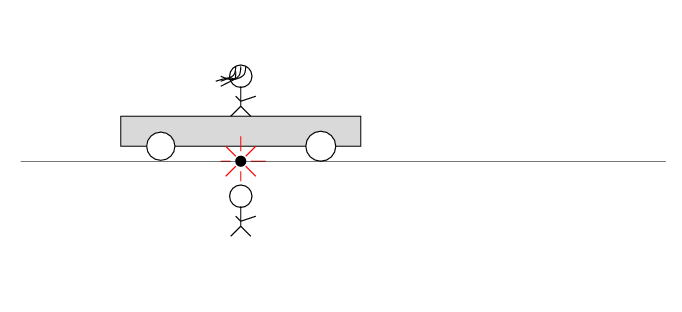
The spark creates light rays that shoot off in all directions at the speed of light. As times passes, the light from the spark reaches greater and greater distances ....
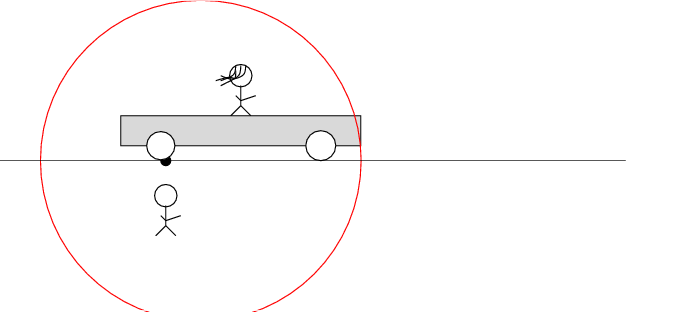
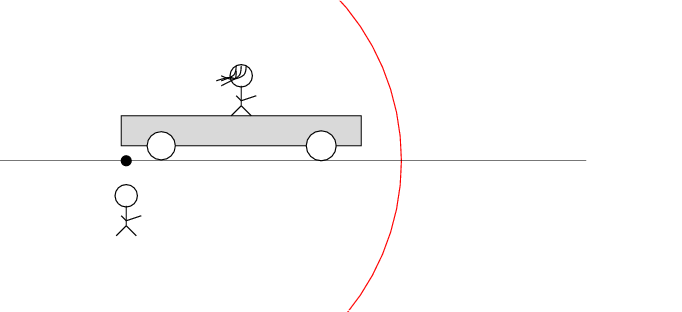
Okay, here comes the puzzle.
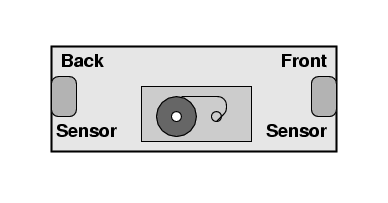
Beth brings her tape deck. Instead of an ON/OFF switch, it has two photosensors, one at each end of the unit. If a bright light strikes both sensors simultaneously, the tape deck will start playing. Beth has inserted a copy of Beethoven's Ninth Symphony into the tape deck.
In Alan's frame of reference ...
Alan stands out in the desert, next to the railroad track. Beth stands on a railroad car, with the tape deck at her feet on the car. The car rolls to the right at speed v.
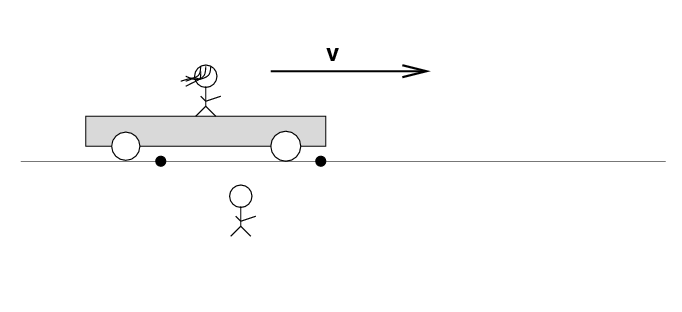
There are two loose wires on the track. Just as Beth passes Alan, a spark jumps from each wire to a wheel of the car.
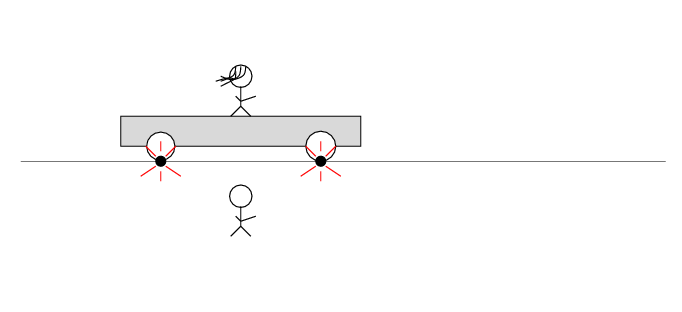
The spark creates light rays that shoot off in all directions at the speed of light. As times passes, the light from the spark reaches greater and greater distances ....
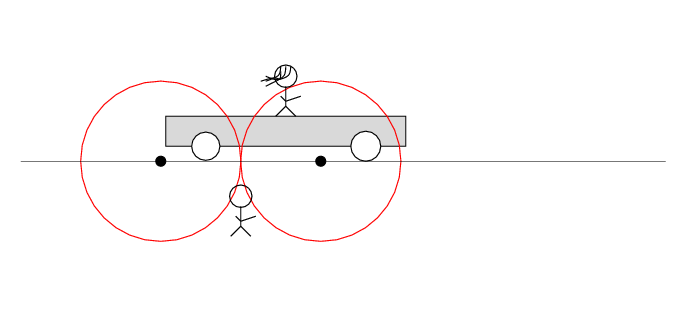
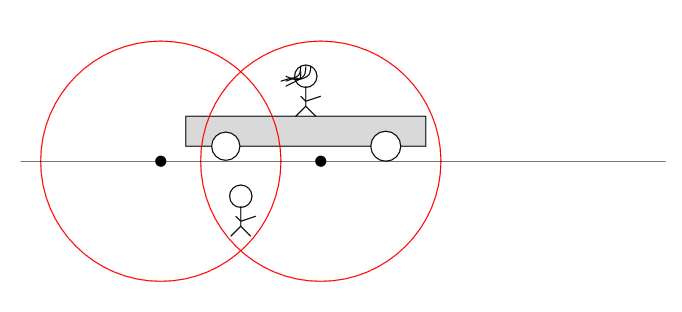
Q: Does the tape deck start to play?
In Beth's frame of reference ...
Beth stands on a railroad car with the tapedeck at her feet on the car. Alan stands out in the desert, next to a railroad track. Alan and the desert move past Beth to the left at speed v.
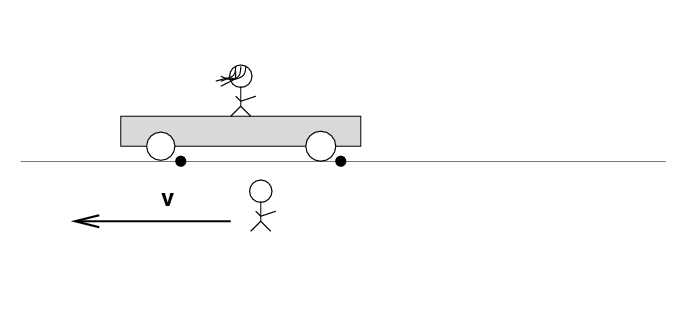
There are two loose wires on the track. Just as Alan passes Beth, a spark jumps from each wire to a wheel of the car.
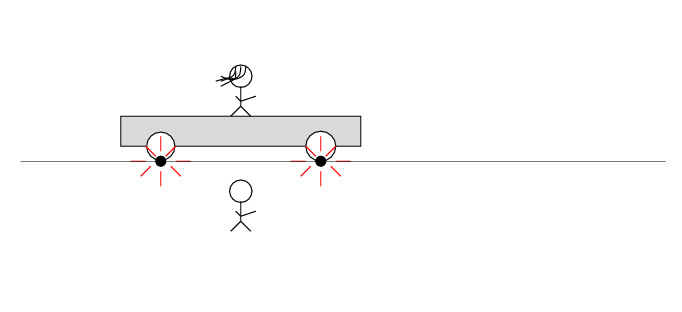
The spark creates light rays that shoot off in all directions at the speed of light. As times passes, the light from the spark reaches greater and greater distances ....
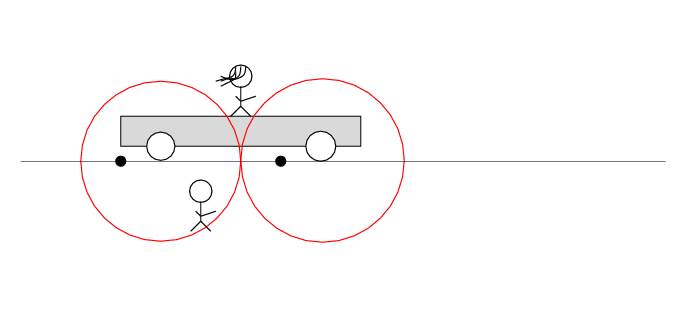
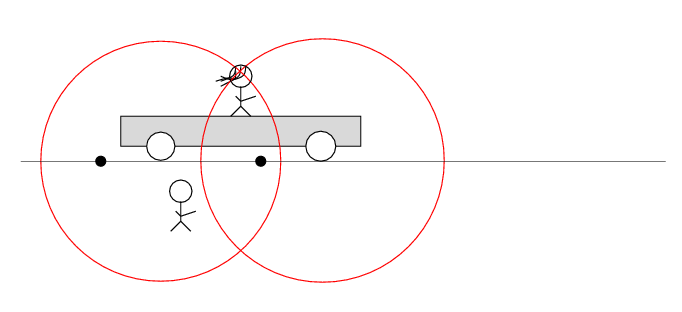
Q: Does the tape deck start to play?
The railroad car comes to a halt a short distance down the track. Beth grabs her tape deck and hops off the car onto the ground. She and Alan walk towards each other. They meet.
Q: Is the tape deck playing?
Maybe this will make some sense if we apply the Lorentz transformations. Let's put some nice, round numbers into the situation, too.
Alan's coordinate system is centered on him, so he stands at x = 0 m. Alan and his assistants measure the position of the two loose wires to be x1 = -10 m and x2 = 10 m. He and his assistants measure the time at which the sparks occur. They determine that the sparks are simultaneous, both occuring at time zero. So t1 = 0 m and t2 = 0 m.
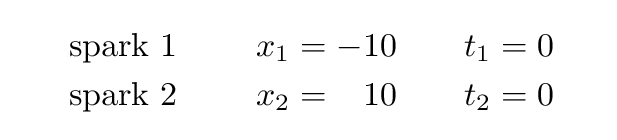
Beth and her assistants roll past Fred at a speed of v = 0.5c. They decide that the moment when Alan passes Beth will be t' = 0 m, and they measure all distances relative to Beth, so she stands at x' = 0 m. Can you figure out the space and time coordinates for these two events, according to Jane and her team?
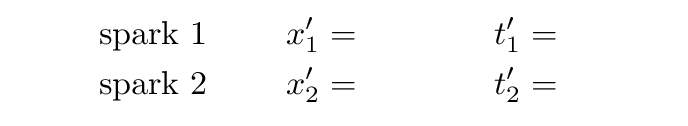
You should discover one of the fundamental aspects of special relativity: events which are simultaneous in one reference frame may not be simultaneous in a different reference frame.
So, here's the sequence of events from Alan's point of view, in which the sparks occur simultaneously. Note that the light waves from the right-hand spark reach Beth and her tape recorder before the light waves from the left-hand spark. Alan concludes the tape recorder does not play.
And here are the same events as measured by Beth and her assistants. Note that
Beth also concludes the tape recorder does not play.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.