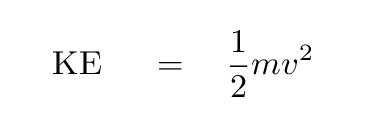
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
What's wrong with the good old expression for kinetic energy?
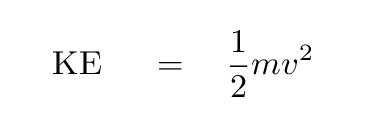
Well, let's do a couple of calculations and see what happens. Suppose we place a proton m = 1.67 x 10^(-27) kg into a particle accelerator and give it lots of kinetic energy.
Q: If we give the proton a KE of
3 x 10^(-11) J = 0.19 GeV
then what is its velocity?
Q: If we give the proton a KE of
9 x 10^(-11) J = 0.56 GeV
then what is its velocity?
You may recall that the LHC accelerates protons so much that they have 7 TeV = 7000 GeV of kinetic energy. Does that mean that the protons are travelling at many times the speed of light?
No!
It turns out -- you can read Taylor and Wheeler for one explanation, if you wish -- that there is an expression for kinetic energy which remains valid even in the relativistic regime:
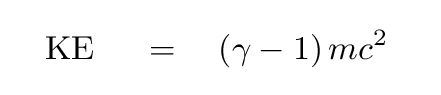
Recall that gamma is defined as
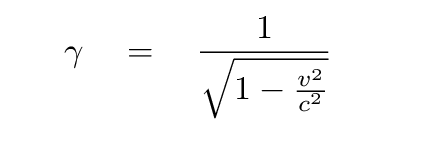
Q: What if the velocity of an object is small
compared to the speed of light?
v << c
As you will see in a moment, it is sometimes useful to reverse this equation in order to write the velocity of an object as a function of the gamma factor.
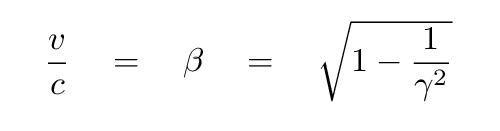
Let's use this expression and again look at the behavior of a proton given large amounts of KE.
Q: If we give the proton a KE of
3 x 10^(-11) J = 0.19 GeV
then what is its velocity?
Q: If we give the proton a KE of
9 x 10^(-11) J = 0.56 GeV
then what is its velocity?
Q: If we give the proton a KE of
7 TeV = 7000 GeV
then what is its velocity?
The relativistic expression for kinetic energy resolves some problems -- it seems to keep protons and electrons with large KE from exceeding the speed of light -- but it doesn't take care of everything. For example, consider the radioactive decay of a neutron.
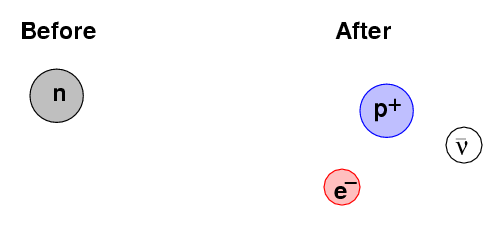
Isolated neutrons will decay after a short time (the half-life of the decay is around 15 minutes) into several different particles -- a proton, an electron, and an anti-neutrino. However, the decay products are not at rest; instead, each particle flies away from the original neutron at high speed:
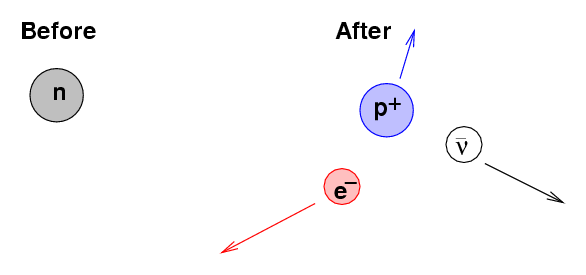
Q: What is the original KE of the neutron?
What is the final KE of the daughter particles?
Is KE conserved?
In general, in radioactive decay, in fission, and in fusion, or in any interaction between sub-atomic particles which involves a change in the number and type of the particles, KE is NOT conserved. Hmmm.
However, if one assigns a certain amount of rest energy to each particle, according to the formula
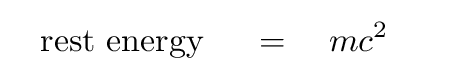
then defines the total energy of a particle to be the sum of its rest energy and kinetic energy
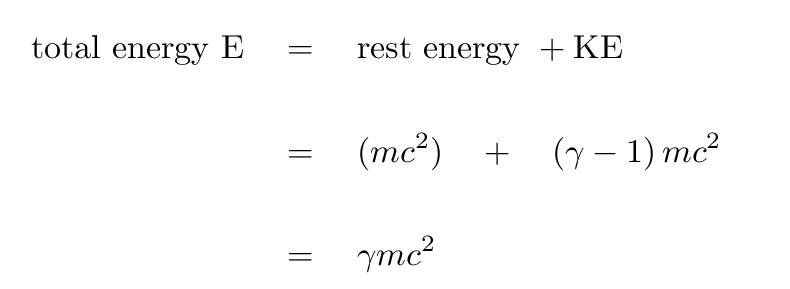
then, when one again looks at radioactive decay, one finds that the total energy IS conserved.
For example, the element polonium-210 (used recently to assassinate Alexander Litvinenko) decays into lead plus a helium nucleus:
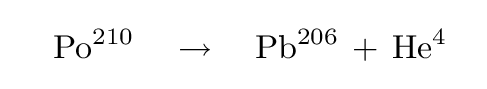
The masses of these particles are usually given in atomic mass units (u). One "u" is equal to 1.660539 x 10^(-27) kg.
nuclide mass (u) mass (kg) --------------------------------------------------- Po-210 209.9828737 3.4868471 x 10^(-25) Pb-206 205.9744653 3.4202859 x 10^(-25) He-4 4.0026033 6.6464779 x 10^(-27) ---------------------------------------------------
Q: What is the difference in mass between
the original Po-210 nucleus and the
two daughter nuclei?
How much KE must the daughter products
carry with them?
Q: Suppose that exactly half of the KE
is given to the helium nucleus.
How much KE does the helium nucleus have?
How fast will it be moving?
Notice the factor of c^2 in the equation for rest energy. The speed of light c is a pretty large number, so its square is a VERY large number. That means that the rest energy of even a small amount of matter can be a significant amount of energy.
Q: Joe has a ordinary can of soda, which
contains about 355 grams of liquid.
If Joe could convert the rest mass of
his soda into energy, how much energy
would be released?
Express your answer in Joules.
Express your answer in kilo-tons of TNT:
1 kTon = 4.2 x 10^(12) Joules.
For comparison, the atomic bomb dropped on Hiroshima released about 15 kTons of energy, and the bomb dropped on Nagasaki released about 20 kTons.
Image of Hiroshima copyright
Hulton-Deutsch Collection
Images of Nagasaki, before and after, in the public domain, hosted on
Wikipedia
An invariant quantity is one that has the same value, no matter which observer is making measurements. The space-time interval
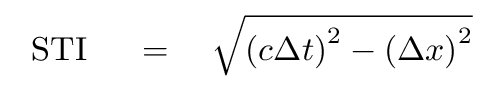
is an example of an invariant quantity.
We know that regular old KE is NOT invariant, but maybe the relativistic total energy is. Let's find out.
The Blue Man throws a ball (m = 0.2 kg ) at a speed of v = 0.5 c to the right.
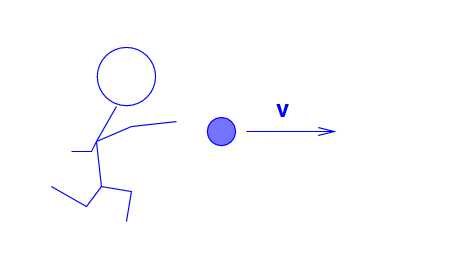
Q: What is the total energy of the ball,
according to the Blue Man?
But the Blue Man and the ball are all travelling across the landscape at a speed of w = 0.8 c, as measured by the Red Men.
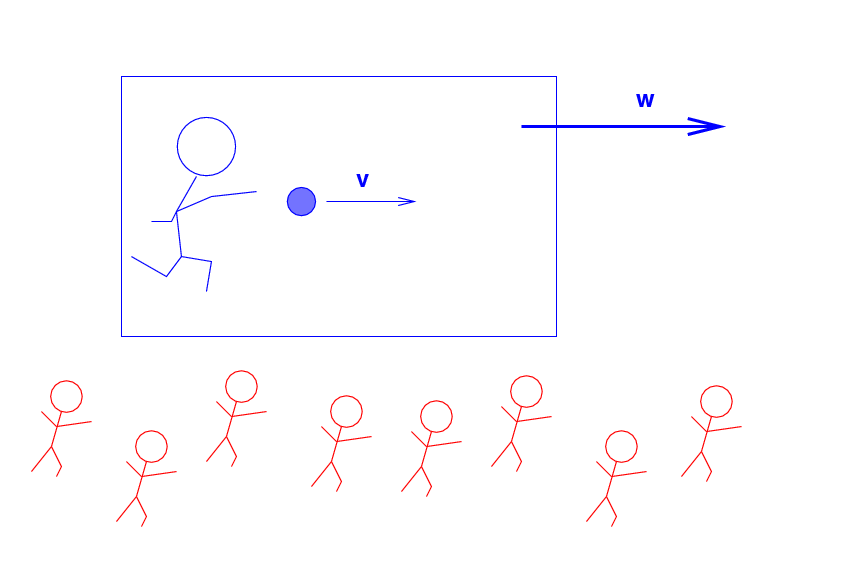
Q: What is the velocity of the ball,
as measured by the Red Men?
Q: What is the total energy of the ball,
as measured by the Red Men?
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.