Inertial frames

Several times in the past few weeks, you may have heard me say an unfamiliar phrase I was describing some aspect of relativity. For example, I may have said,

" ... that the laws of physics are the same in all inertial frames ...

That qualifier is important: the rules of special relativity apply to some situations, but not to all. In order to be sure that you can use special relativity to investigate phenomena, you need to verify that you (and the other observers involved in an experiment) are living in an inertial frame of reference.

What does that mean? There are several ways to describe inertial frames, so let me start by listing just a few.

An inertial frame is one in which ...

you float freely. Taylor and Wheeler use the phrase "free-float" instead of "inertial" quite frequently in their book.
your weight on an ordinary bathroom scale reads ZERO.
if you hold a ball in your hand steady, then release it, it just floats there next to your hand.
if you hold a ball in your hand steady, then toss it gently in any direction, it continues to move in that same direction with unchanged speed.
observers experience no acceleration.
"... every free test particle initially at rest with respect to that frame remains at rest, and every free test particle initially in motion with respect to that frame continues its motion without change in speed or direction." (from Taylor and Wheeler, Section 2.3)

One clearcut example of an inertial reference frame is an isolated spaceship, far, far away from the Earth, the Sun, the Milky Way Galaxy, and all other massive objects.

Fred places a blue ball into a claw at the left end of the ship, and red ball into a claw at the right end of the ship. The claws hold the balls motionless.

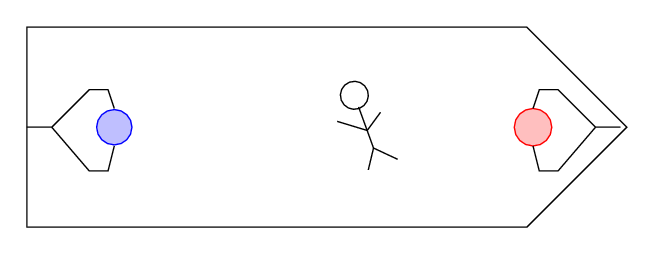
Then Fred pushes a button which opens both claws.



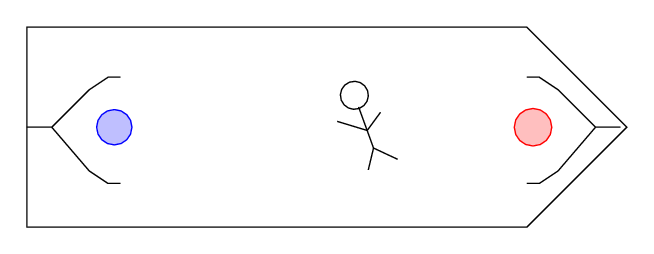
  Q:  What happens to the balls after they are
      released?

The balls just remain in their positions, floating freely, just as Fred floats in the middle of the ship. This spaceship is an inertial frame of reference.



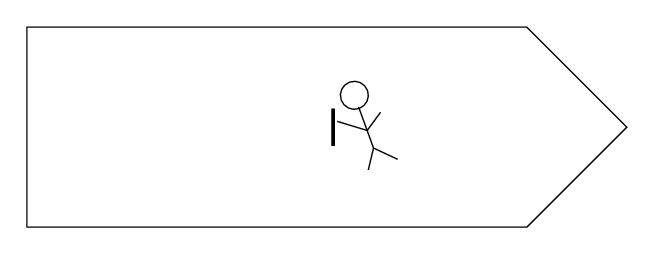
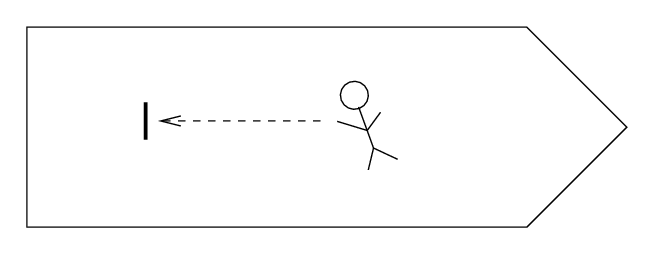
  Q:  Suppose Fred tossed his pencil gently
      towards the left end of the ship.  
      What path would it follow?

The pencil would move in a straight line to the left, with a constant speed.

What good are inertial reference frames?

The main reason for being so picky about inertial reference frames is that life becomes much, much simpler for physicists who conduct experiments and make measurements in inertial frames. Einstein's Postulates of Special Relativity are

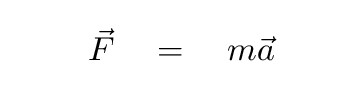
The Laws of Physics are the same within all inertial reference frames. That is, for all observers in any inertial reference frame who watch a ball flying through space,
The speed of light in a vacuum is the same for all observers in inertial reference frames.

Just because the laws of physics are the same in all inertial frames doesn't mean that all the measured quantities are the same. For example,



      SAME in all                NOT the same in all
     inertial frames               inertial frames
------------------------------------------------------------
     laws of physics                speed of an object

     speed of light                 forces on an object

     charge on electron             space interval between two events

     Avagadro's number              time interval between two events
    
     space-time interval            length of an object
       between two events
--------------------------------------------------------------

Is an ordinary lab on Earth an inertial frame?

Fred stands in a spaceship-shaped laboratory on the surface of the Earth. He places balls into two claws at opposite ends of his lab. The claws hold the balls motionless.

Then Fred pushes a button which opens both claws.



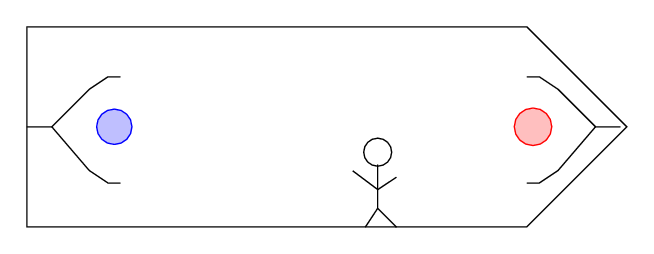
  Q:  What happens to the balls after they are
      released?

The balls fall to the floor, of course, just as Fred is pulled to the floor by the gravitational force of the Earth. This lab on the surface of the Earth is not an inertial frame of reference (for ordinary, everyday events).

What about a ship in orbit around the Earth?

Fred takes his spaceship-shaped lab into orbit around the Earth.



  Q:  Is the gravitational force on Fred 
      due to the Earth equal to zero?

No, the gravitational force on Fred due to the Earth is not zero. If Fred is in a typical low-earth orbit, at altitude 200 km above the surface, and if Fred has a mass of 70 kg, then the gravitational force on him is:



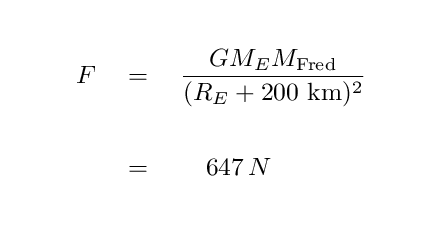
  Q:  How does this compare to the gravitational
      force on Fred when he is standing on the
      surface of the Earth?

Now, what happens if Fred performs the ball-and-claw experiment again?

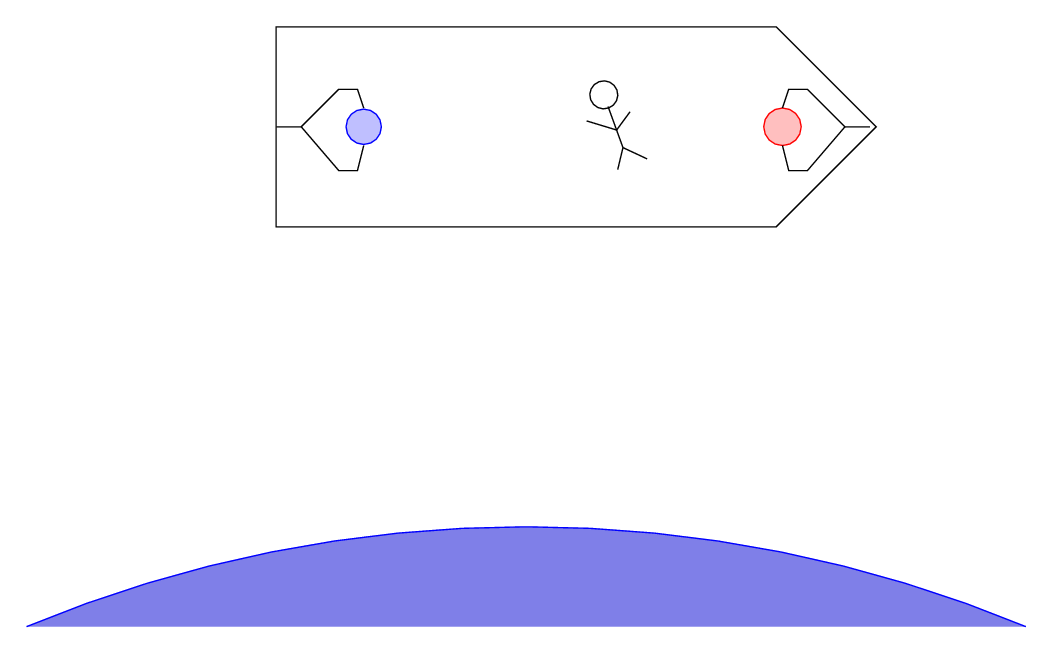
When the claws release the balls, they will each feel a gravitational force towards the Earth.



  Q:  Why don't the balls fall to the bottom
      of the spaceship?

The answer is ... that they _do_ fall towards the bottom of the spaceship, but the spaceship itself is also falling, in the same direction (towards the Earth) and at the same rate (about 9.2 meters per second per second). Since the spaceship is falling just as fast as the balls are falling, the balls don't appear to move towards the walls of the spaceship.

Fred, floating inside the spaceship himself, observes the balls to hover motionless in mid-air when the claws release them. He concludes that he is in an inertial frame of reference.

Inertial frames may be limited in extent

Fred gets rid of the spaceship and settles for a simple rectangular laboratory. He asks his friend Steve to lift it up 10,000 meters above the surface of the Earth with his big green balloon.

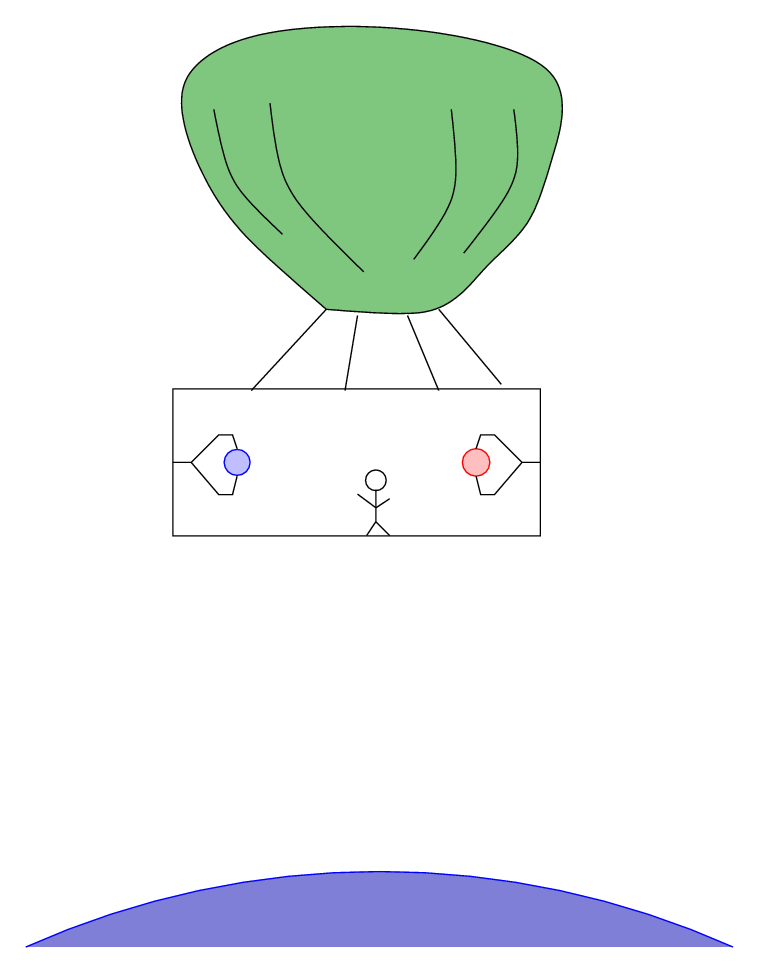
When Steve cuts the cords, Fred and the lab start to fall towards the Earth. The two balls are held a distance L = 20 m apart by the claws. As they are falling, Fred presses the button which opens the claws.



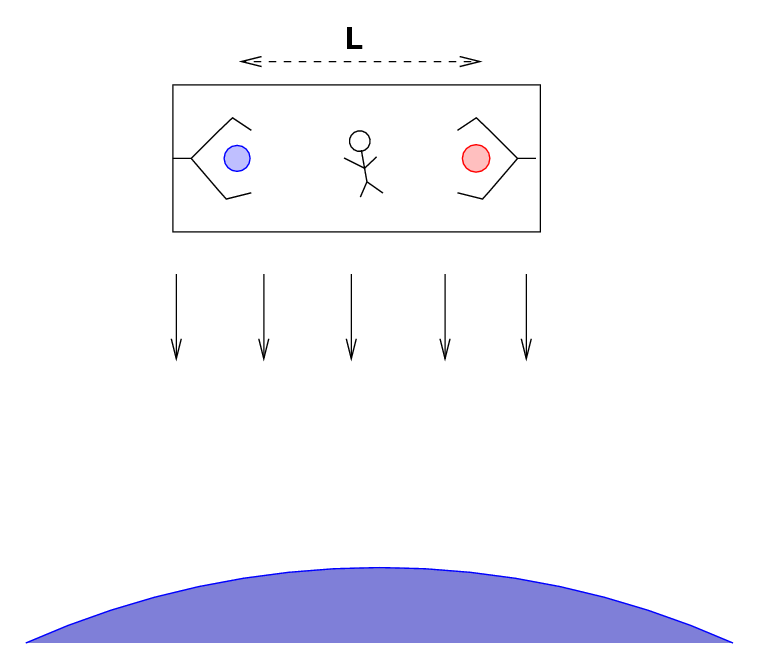
  Q:  What happens to the two balls?

It turns out that the answer to this question is not completely obvious. There are two possibilities, depending on the precision of the measurements Fred can make.

Fred watches with his eyes for 10 seconds

As far as Fred can tell, the two balls remain in their original positions. He would say, "Each ball floats motionless in its original position. The initial distance L = 20 m remains unchanged. Since objects which are initially at rest remain at rest, I am in an inertial frame."

Fred takes pictures with micro-focusing cameras over 20 seconds

The cameras can record the position of each ball to a fraction of a millimeter. Over the course of 20 seconds, they indicate that the two balls move towards each other slightly .... and, as time goes on, their approach accelerates.

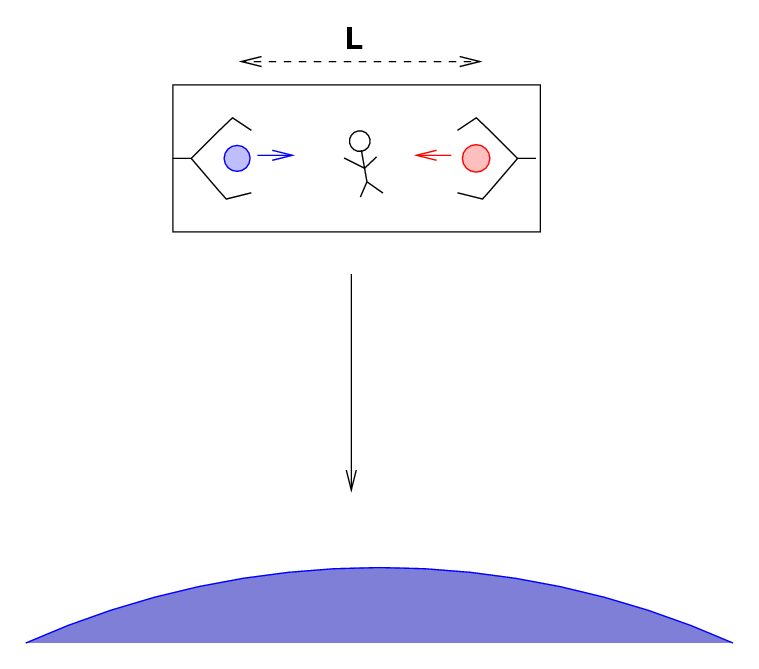
Why? The answer becomes obvious if we take a look from a large distance.

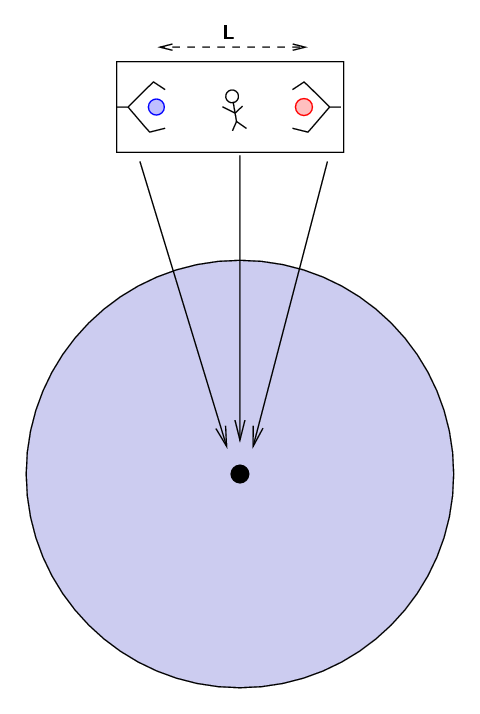
Fred and each of the two balls are falling straight down towards the center of the Earth -- but "straight down" isn't exactly the same direction. Their falling paths converge as they approach the center of the Earth.

One way to figure out exactly how fast the balls approach each other is to use some geometry.


   
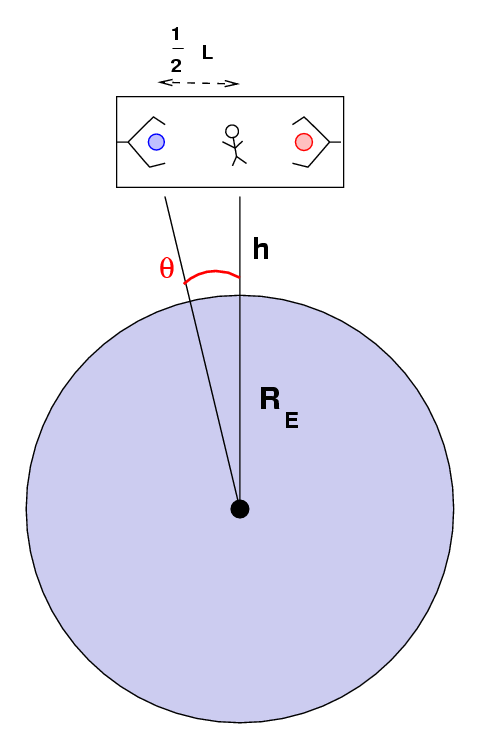
    Q:  When the cords are first cut,
        what are

            h   =  height above ground (m)

           R_E   =  radius of Earth (m)

         1/2 L  =  distance from blue ball to Fred

            θ   = angle between blue ball and Fred




    Q:  After 20 seconds, the lab has fallen 
        a distance 1960 meters, so that its   
        height above the ground is only 
        h = 8040 meters.

        How far is the blue ball from Fred now?

        How far is the blue ball from the red ball now?

Because he sees each ball accelerate from its initial state of rest, Fred concludes that he is NOT in an inertial reference frame.

So, depending on the instruments Fred uses, and the duration of his experiment, Fred might conclude that his laboratory IS or IS NOT an inertial frame.

When you are analyzing a situation, one of the things you must do is to figure out the limits to which you are measuring phenomena. To what extent is your reference frame an inertial frame?

Consider an experiment you have seen before. Fred stands on the floor of his lab, on Earth. On the table next to him is a tube of length L = 5 m. A proton moving at v = 0.5 c shoots out of a nearby particle accelerator and flies through the tube. Devices at each end of the tube measure the time at which the proton enters, then exits, the tube. The instruments are very sophisticated, so that they can measure these events to high precision.



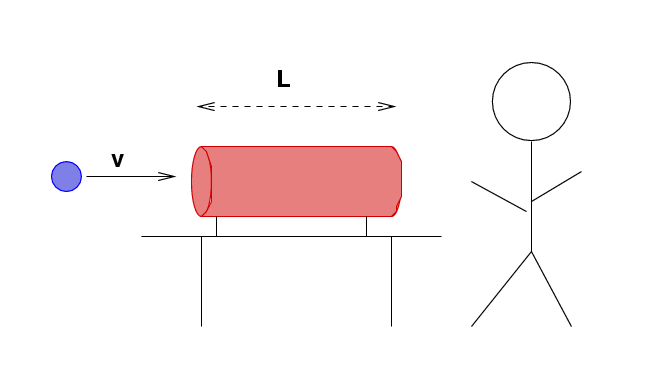
  Q: Can we consider Fred's lab an inertial
     reference frame for this experiment?


  Q: What is the time interval between the
     two events (entering tube, exiting tube)?


  Q: How far does the proton move horizontally
     during that interval?


  Q: How far does the proton move vertically
     during that interval?

What would happen if Fred was measuring the motion of a baseball? Would his measurements qualify as made in an inertial reference frame?

For more information

See Taylor and Wheeler, Spacetime Physics