How to write equations representing actors in space-time

Now, consider the following actors and events.

Oscar sits in his chair at location x = 1 ns and does not move.
Ralph walks to the right at a speed of β = 0.40. At time t = 0 ns, Ralph is at x = -10 ns.
Lorraine jogs to the left at a speed of β = -0.80. At time t = -5 ns, Lorraine is at x = 15 ns.
At time t = 0 ns, Oscar shoots a laser to the right.

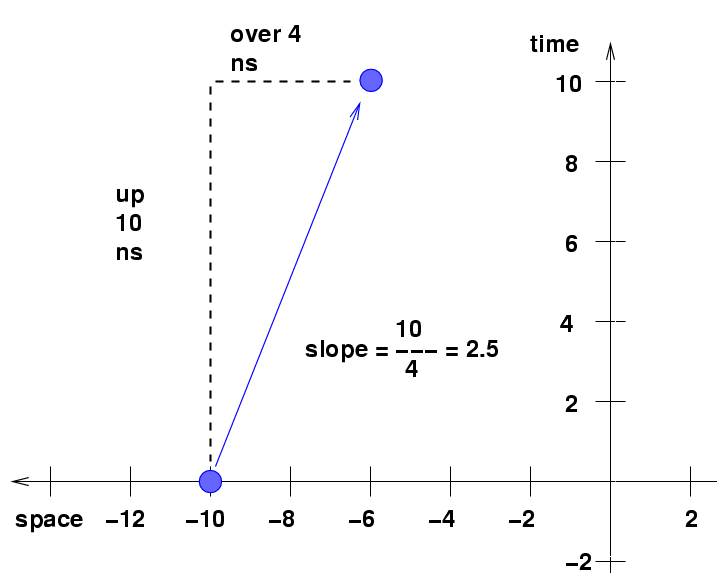
Consider Ralph. How can we write an equation which represents his path through space-time? We need to connect space x and time t by means of some mathematical operations.

There are several ways to do it. One way is to look at Ralph's path in the space-time diagram. We know that he moves with a speed of β = 0.4, so that the slope of his path in the space-time diagram should be


                         1          1
     slope of path  =   ---   =   -----     =   2.5
                         β         0.4

We are told that he is at a particular location (x = -10 ns) at a particular time (t = 0 ns). Therefore, we can draw his path on a graph pretty easily: start at the location (-10, 0), and draw a line moving to the upper right with a slope of 2.5.

To write the equation of this line in the usual form,

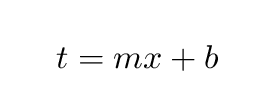
we need to know the slope and the y-intercept. The slope we do know already.

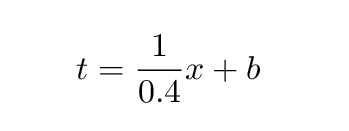
The y-intercept of this line is the location at which it crosses the x-axis. I can do a little algebra, or draw a line carefully on a piece of paper, to see that this line will cross the y-axis at t = 25 ns. That means that the equation of the line is

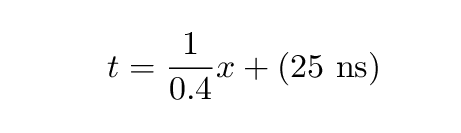
Now, in most circumstances, physicists like to describe motion as "where is something as a function of time." In other words, we usually write equations of motion that look something like this:

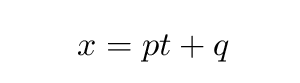
It is possible to analyze the motion of objects in space-time diagram using this choice, too. Ralph, for example, moves 0.4 ns in space for every 1.0 ns of time which passes. So the factor by which we multiply changes in time to find changes in space is just 0.4.

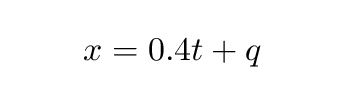
Now, we can use the information given to us to find the equivalent of the "y-intercept" for this equation. The fact that Ralph was at position -10 ns when the time was t = 0 ns tells us that the constant term q = -10 ns. So the path Ralph makes through the space-time diagram can also be written this way:

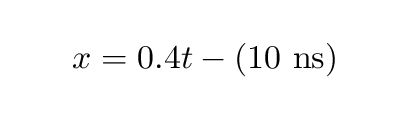
You can choose either form to solve problems: they are exactly equivalent. If you wish, you can use some algebra to derive one from the other.