Time dilation

You've already seen that observers in inertial frames moving at different speeds may not measure the same time between two events. Let's look at this notion of time dilation in some detail today. We'll begin by using the space-time interval as our tool.

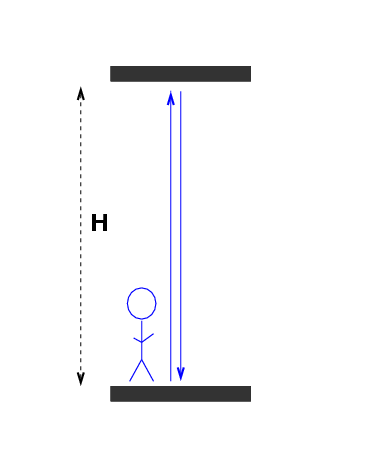
The Blue Man lives in a Blue Room. He places a laser on the floor, pointing straight up towards his ceiling, which is H = 10 m above him. There's a mirror on the ceiling. The Blue Man runs an experiment in which he measures two events:

he sends a flash of light from the laser beam upwards
the reflected beam comes back and strikes a photo-detector on the floor


  
  According to the Blue Man,

   1.  What is the space interval between these 
       two events?

   2.  What is the time interval between these
       two events?

   3.  What is the space-time interval between
       these two events?

Now, the Blue Man and his Blue Room are flying across the landscape at a very high speed. They fly past the Red Man and his army of Red Minions, all of whom have metersticks, notebooks, and synchronized watches. The Red Army observes this same experiment, and makes its own measurements of the two events. They determine that the Blue Room moves a distance L = 8 m as the light beam rises towards the ceiling, and another L = 8 m as the light beam reflects back to the floor.


  
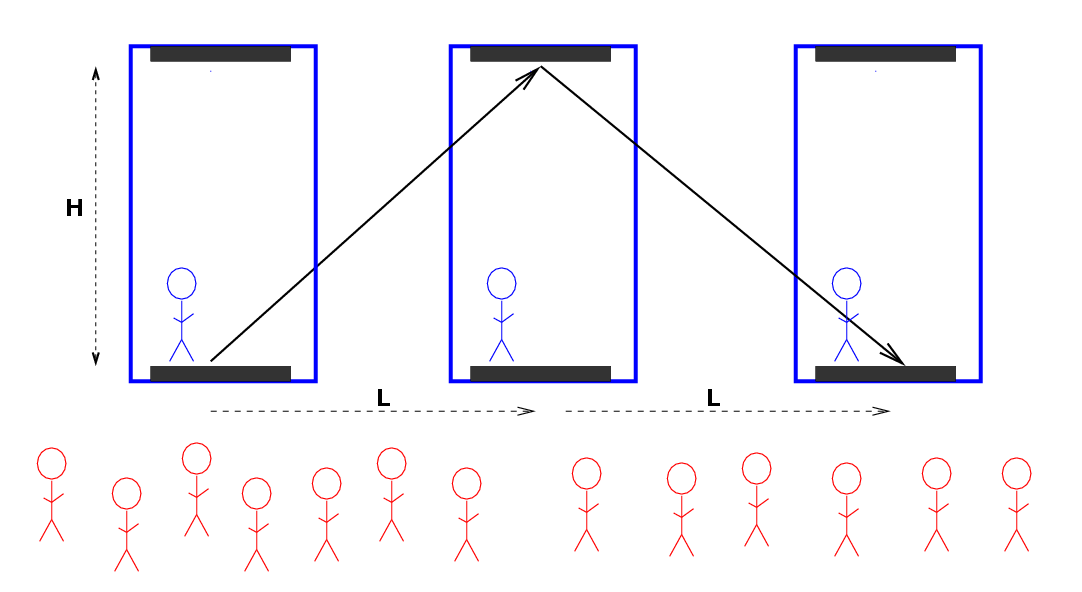
  According to the Red Man,

   1.  What is the space-time interval between these 
       two events?

   2.  What is the space interval between these
       two events?

   3.  What is the time interval between
       these two events?

So, according to these two inertial observers, the same events have a different time interval. If you were to ask the Red Man, he might say,

My clock is perfectly fine. The fact that the Blue Man measures a shorter time interval means that his clock is running more slowly than my clock.

Is there some simple relationship between the relative speed of two observers and the relative rates of their clocks? Using the space-time interval will allow us to find the time intervals correctly, but it can be cumbersome at times. In particular, it requires measurements of time intervals and space intervals between discrete events.

But what if there aren't any measurements of specific events? What if you simply want to know the relative rates of clocks in two reference frames which are moving relative to each other at some given speed?

Let's try a different way to look at the same experiment. In particular, let's focus on finding a way to calculate the time dilation as a function of the relative velocity v of the two frames of reference.

Here's a diagram showing the Red Man's view of the experiment again. I've simplified things a bit.

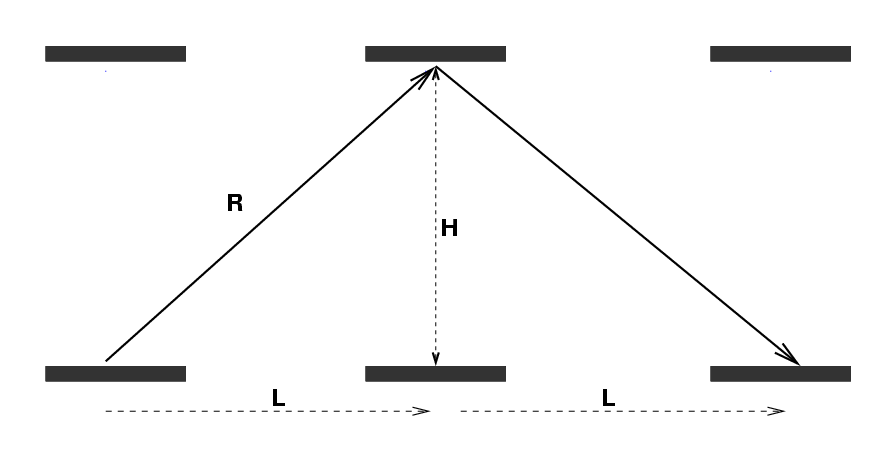
We can replace the distance L with an expression that involves the time interval in the Red Man's frame of reference.

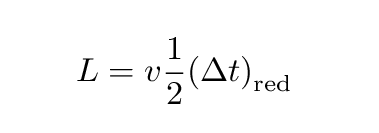
The distance of the light path along the hypotenuse of this triangle must be

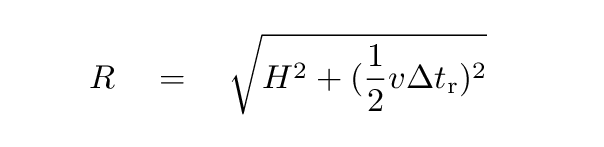
During the interval between events 1 and 2, the light beam travels a distance of 2R. So, we could express the time interval between the two events in the Red Man's frame of reference as


  
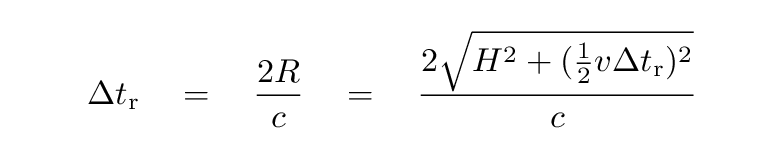
  Q:  Can you solve this equation to find 
      the time interval measured by the Red Man
      in terms of H, c, and v?

You should end up with

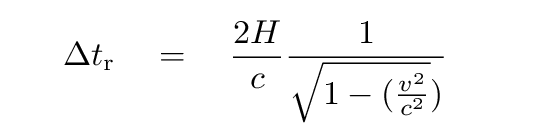
This particular combination of v and c appears so frequently in special relativity that physicists have given it a name of its own: "gamma":

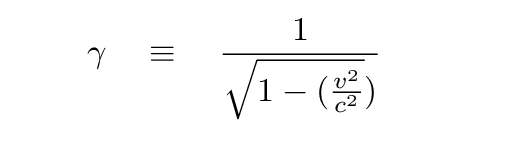
Notice the relationship between the two time intervals measured by the Blue Man and the Red Man.





  
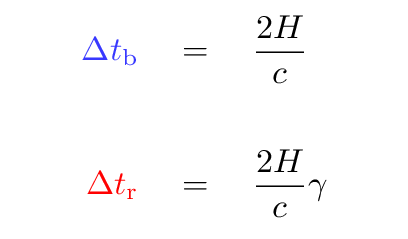
  Q:  Suppose that the speed of the Blue Room
      is v = 0.625 c.  What is the value of
      gamma?  


          a)   1.28
          b)   0.78
          c)   1.63

      
  Q:  Recall that H = 10 m.  What is the time
      interval between these two events
      according to the Red Man?    What is 
      the time interval according to the 
      Blue Man?


          a)    Blue Man says 20 m     Red Man says 20 m
          b)    Blue Man says 20 m     Red Man says 25 m
          c)    Blue Man says 20 m     Red Man says 16 m

If you ask the Red Man about this difference in time, he might say,

My clock is perfectly normal. The fact that the Blue Man measures a smaller time interval between the two events means that his clock is running more slowly than my clock; in fact, it is running at a rate which is gamma times slower than my clock.

Tests of Time Dilation

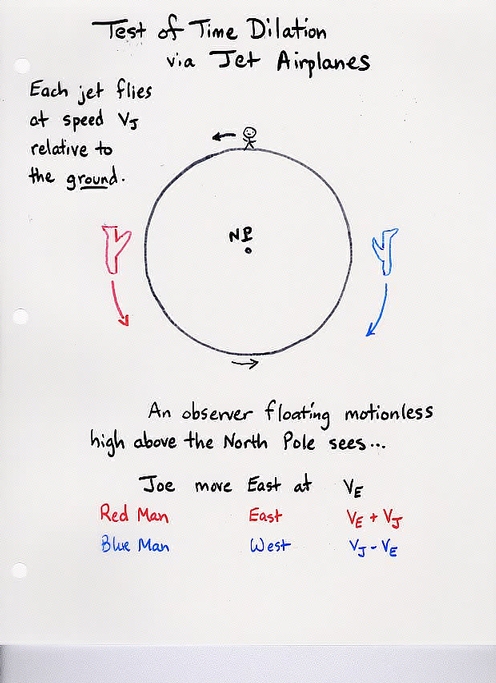Viewgraph 6


 Assume that planes fly at about 500 mph = 250 m/s
 relative to the ground.

      Q1:   How long does it take a plane to fly around
            the world?


      Q2:   According to the stationary observer floating
            above the North Pole,

               what is the gamma factor for Joe?

               what is the gamma factor for red plane?

               what is the gamma factor for blue plane?


      Q3:   What is the difference between Joe's watch 
            and the red plane's clock when they meet?

      Q4:   What is the difference between Joe's watch 
            and the blue plane's clock when they meet?

Calculating the gamma factor for ordinary speeds v much less than the speed of light can be tricky; some calculators can't handle numbers which are very, very close to 1. Read this example of calculating gamma for a few tips.

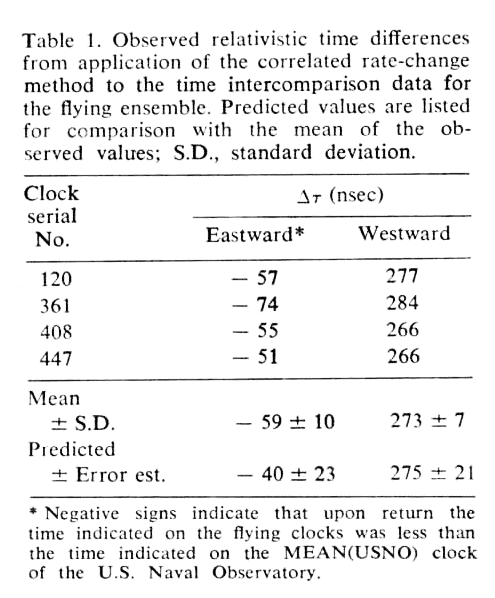
There's a more recent test of time dilation, this time using individual atoms rather than airplanes.

Read about the test of special relativity by Chou et al. from 2010

For more information

See Taylor and Wheeler, Spacetime Physics
Around-the-World Atomic Clocks: Predicted Relativistic Time Gains, by J. C. Hafele and Richard E. Keating, Science, vol 177, p. 166, July 14, 1972.
Around-the-World Atomic Clocks: Observed Relativistic Time Gains, by J. C. Hafele and Richard E. Keating, Science, vol 177, p. 168, July 14, 1972.