 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
As you've heard earlier, the cloud of gas and dust which turned into our solar system transformed itself from an initially spherical-ish shape into a flattened disk. The planets and (most of) the asteroids and (some of) the comets orbit the Sun in roughly the same plane.
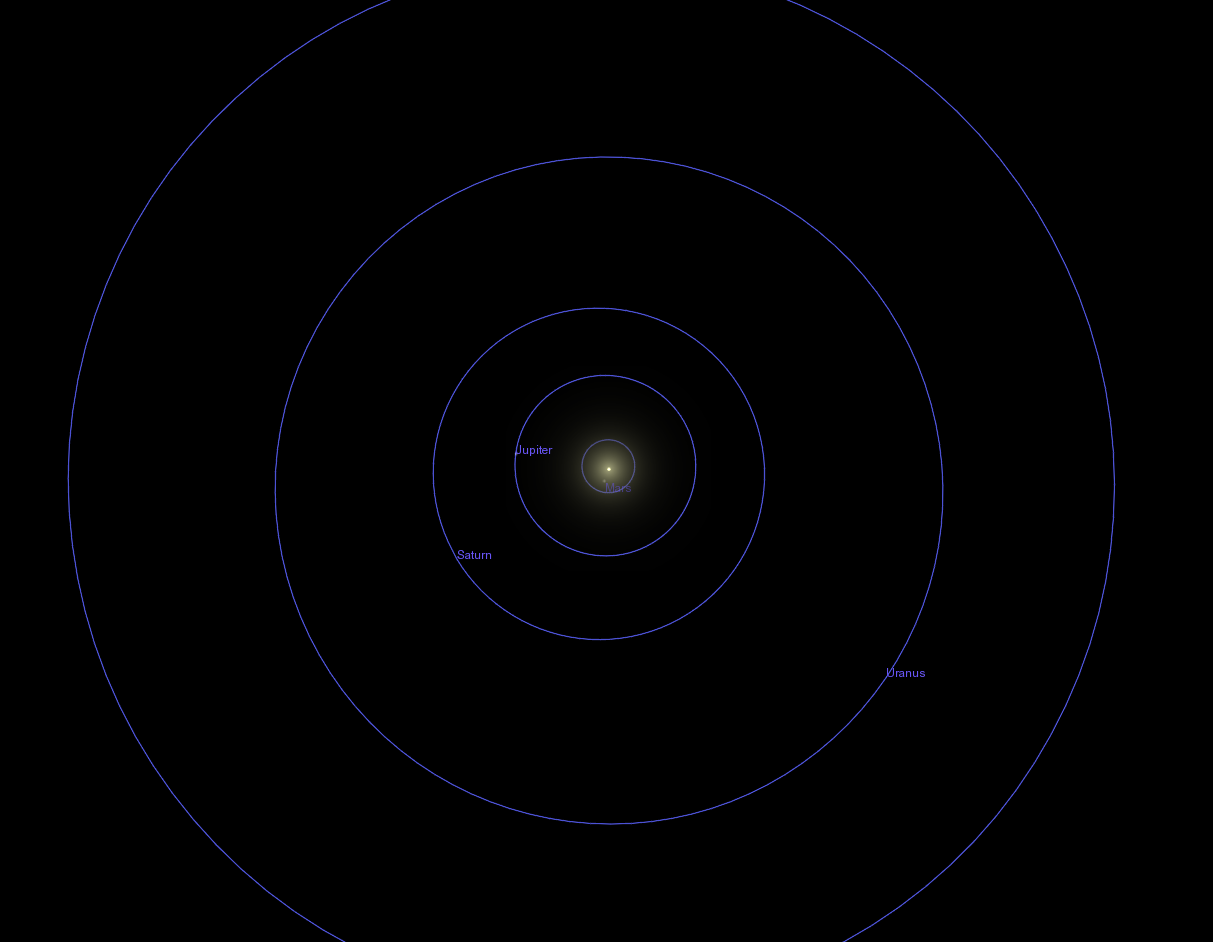
In other words, when seen from above, the Solar System looks like this:

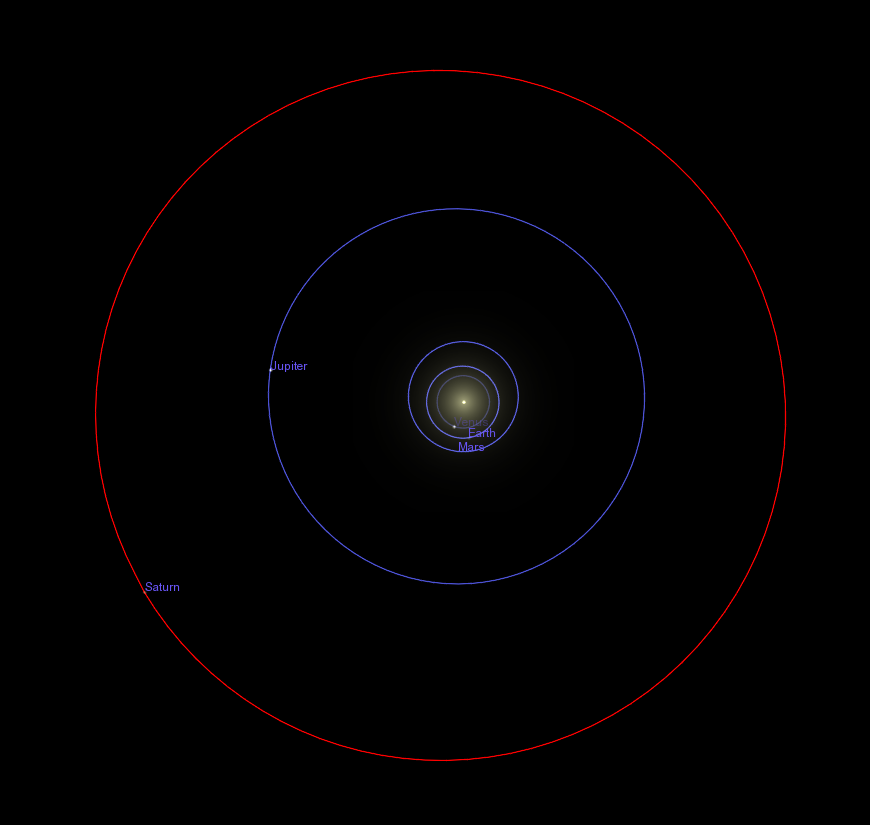
But when viewed from the side, like this:

Q: Can you put these in order by their flatness?
a) Solar System (major bodies only)
b) 12-inch vinyl LP record
c) pancake
It turns out that the solar system lies in the middle.
So, yes, the Solar System is (mostly) flat.
Yes, if we include those crazy comets and some unusual asteroids, it's not quite so flat.
But is it round?
For millenia, astronomers have known that bodies moving in the solar system trace out curved paths. But are those paths circles -- TRUE circles -- or some other round-ish shape?
If you could fly up above the plane of the solar system and look down, and if the planets really did leave trails behind them, then you might simply examine the shape of these trails carefully. I've used the software package called Celestia to take a simulated picture from a vantage point far above the Sun.
Q: Is the orbit of Saturn a perfect circle?
Hmmm. Perhaps it's not a circle, but some other circle-like shape. One sort of geometric figure which can look very similar to the circle is the ellipse. What is an ellipse, exactly?
Well, both circles and ellipses are conic sections. That simply means that if you start with a cone, and slice it, you can end up with a slice giving either a circle or an ellipse.
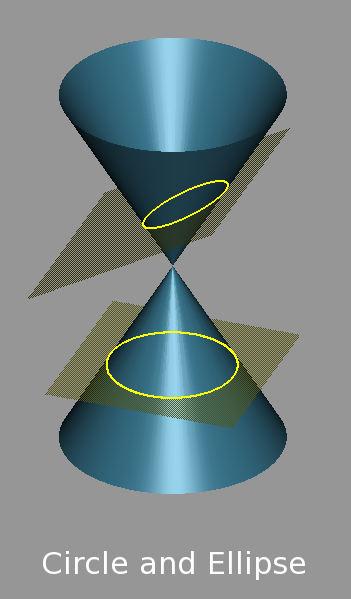
Image courtesy of
Duk and Wikimedia Commons
The eccentricity of an ellipse is a measure of how far from round it is:
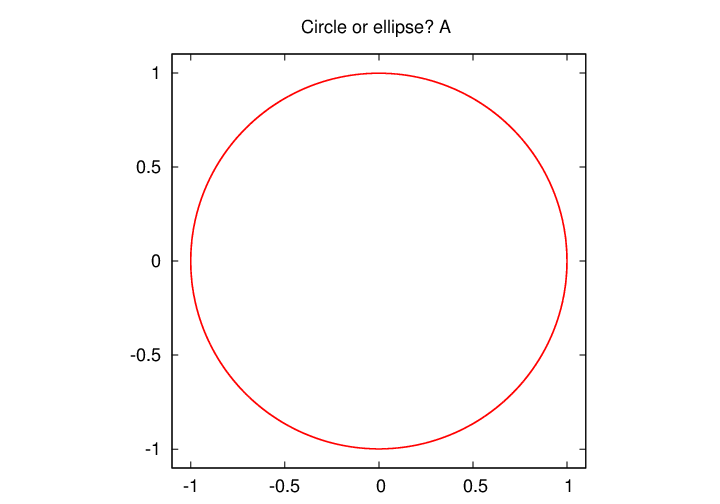
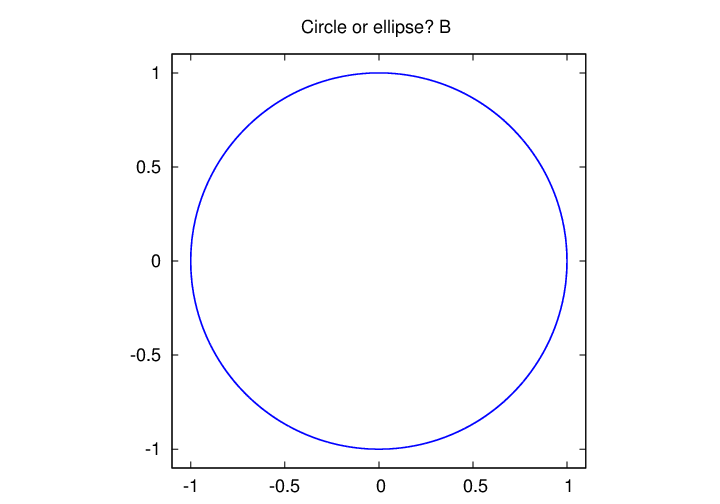
Let's see if you can tell the difference between a real circle and an ellipse with eccentricity 0.5. I'll show two figures, A and B, and you tell me which is the circle and which the ellipse.
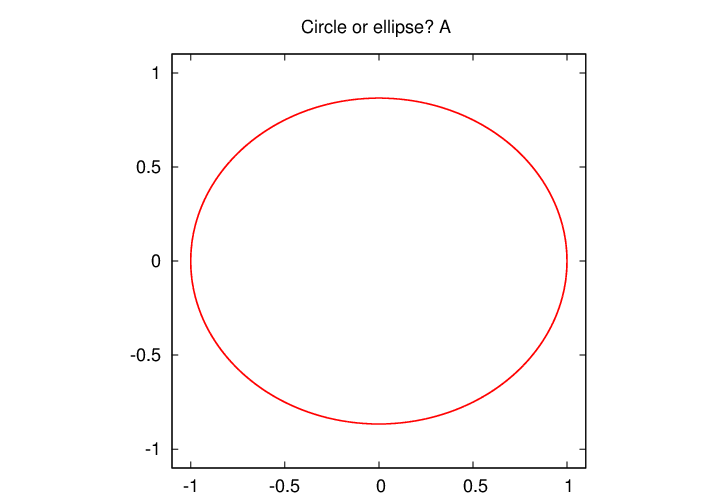
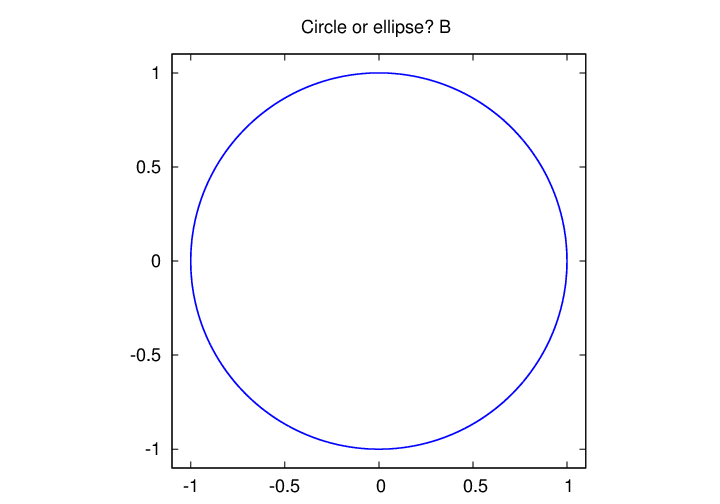
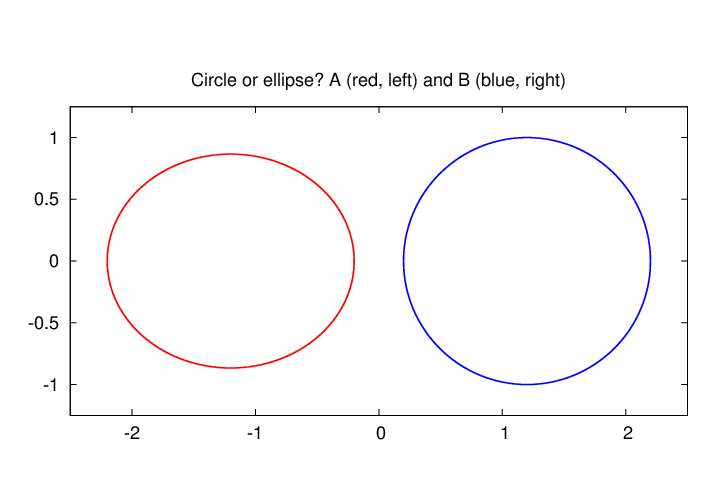
That wasn't very hard.
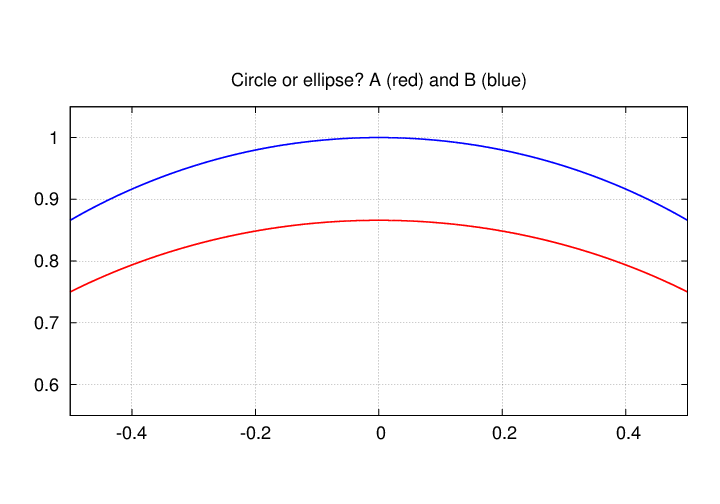
But if the eccentricity is close to 0, then the ellipse looks pretty darn like a circle. The eccentricity of Saturn's orbit is 0.057; can you tell the difference now?
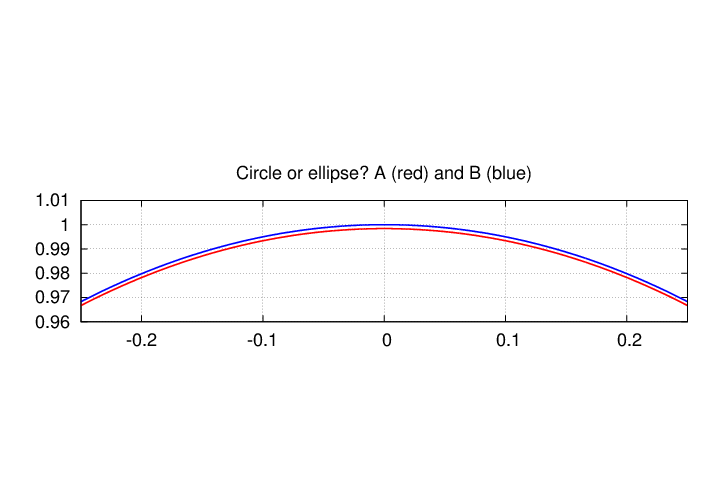
I hope that you can see that the difference between a circle and an ellipse with small eccentricity can be very small. It can be very difficult to distinguish one from the other. A person who _could_ tell the difference, and identify a circular path as being an ellipse with such a small eccentricity, would have to one smart cookie ....
... which Johannes Kepler certainly was:

Image courtesy of
Wikipedia
Kepler was one of the top mathematicians of his time: he was at one point hired to be the imperial mathematician to the Holy Roman Emperor Rudolph II. His speciality was astronomy, and so, as a young man, he went to work for the famous astronomer Tycho Brahe. Tycho used a series of instruments in his observatory to make the most precise measurements of the positions of stars and planets up to his time.
But don't forget: this was before the invention of the telescope. All of Tycho's measurements were made with the naked eye.

Image from Tycho's
Astronomiae instauratae mechanica
courtesy of the
Treasures of the Bodleian Library
Over several decades, Tycho had collected hundreds of measurements of the planet Mars. One of Kepler's tasks was to reduce these measurements and figure out the properties of the red planet's orbit. When Tycho died unexpectedly in 1601, Kepler inherited the books full of these measurements.
Over the next thirty years, Kepler labored over the job of analyzing Tycho's data. His job was a difficult one -- he couldn't simply fly up above the solar system and take a snapshot of the planets! Remember,
It took years of effort ...

Image of Kepler's notebooks courtesy of
Natural Sciences 102 at University of Arizona
but Kepler gradually figured out that the orbit of Mars -- and the other planets in our solar system -- followed three general rules.
What's a focus? There are two foci along the long axis of the ellipse, one on each side of the center. The foci have both special mathematical properties, and special physical properties.
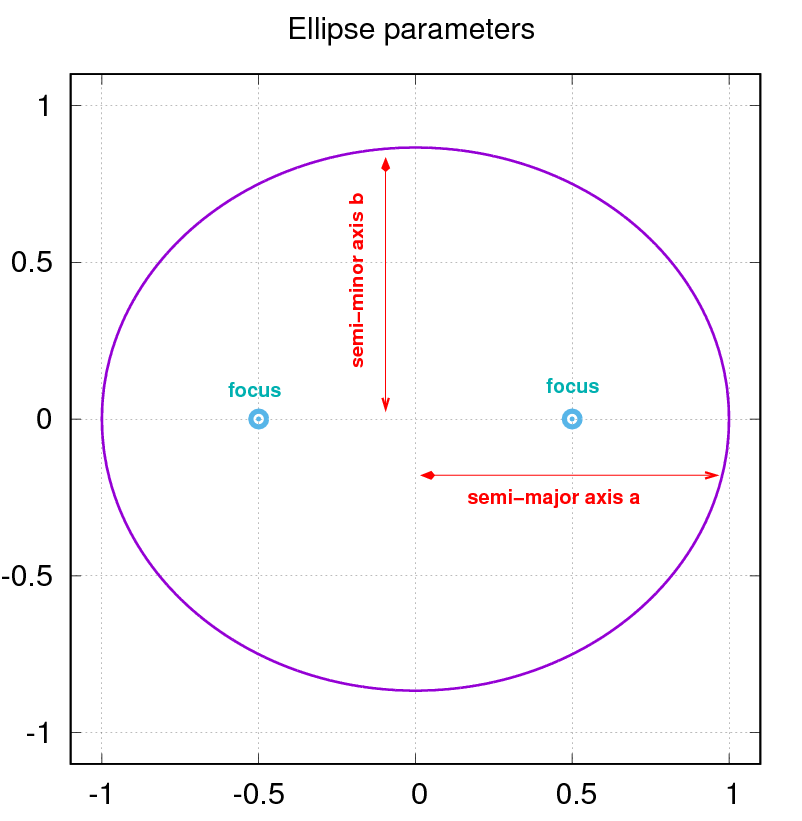
For example, if you stand in an elliptical room, at one focus, and speak, every sound wave radiating away from you will bounce off the curved walls and end up meeting at ... the other focus. You may learn more about foci, and how they can help you to draw an ellipse, in the lab section of this course.
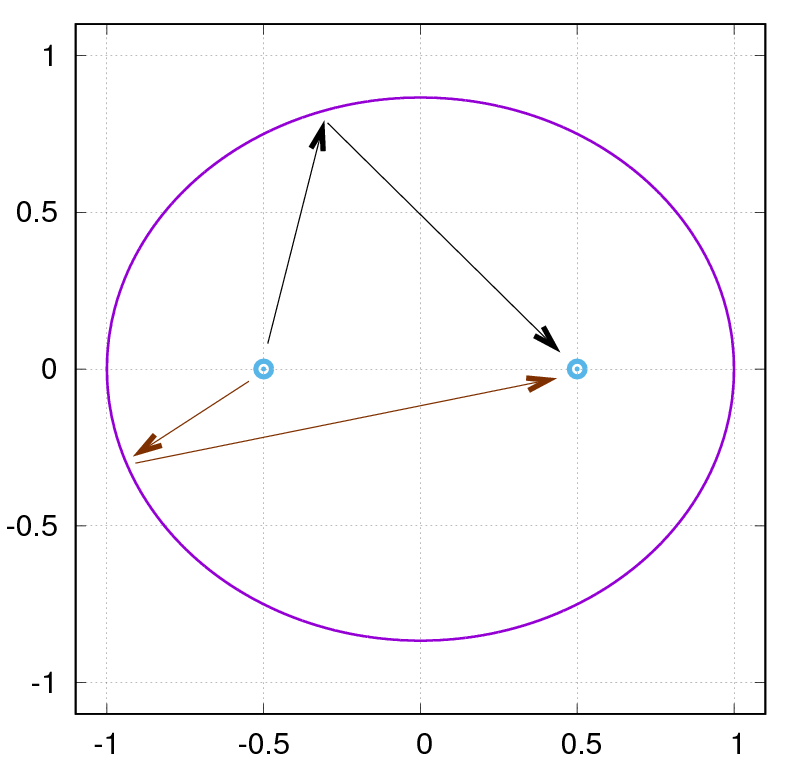
Kepler realized that each of the planetary orbits was not only an ellipse, but also oriented just so that the Sun was located at one of the two foci. The other focus was just empty space. So, as the planets move, they trace out orbits like so:
Before Kepler, all astronomers had assumed that the planets must move in circular orbits. The change to elliptical orbits was a big advance in our understanding of the solar system.
Kepler's Second Law builds on the first. As an object moves in its elliptical orbit, its speed changes.
But it's even more mathematical than that: the object's speed is exactly inversely propertional to its distance from Sun. That means that the region it sweeps out as it moves during some period of time -- each week, or each month -- will always have the same area.

An early, great edition of the
webcomic
XKCD
This change in speed with distance from the Sun may seem reasonable, or even obvious, but it was another big advance by Kepler; up to this point, scientists had always assumed that planets must move with uniform speed everywhere in their orbits.
In addition to his excellence in geometry and mathematics, Kepler had quite the imagination. He constantly sought connections between the realms of the real and the ideal. In his mind, the "music of the spheres" was a real phenomenon; the properties of music might yield insights to the motions of planets in the sky.
Years after publishing his First and Second Laws, Kepler continued to ponder the properties of the orbits he derived from Tycho's measurements. For thousands of years, astronomers had knownn that the planets closest to the Sun -- Mercury and Venus -- had much shorter periods than those farthest from the Sun -- Jupiter and Saturn. But was there any more sophisticated pattern to these numbers?
Planet a = distance from Sun P = period of orbit
(semi-major axis)
(AU) (years)
-------------------------------------------------------------
Mercury 0.39 0.241
Venus 0.72 0.615
Earth 1 1
Mars 1.52 1.88
Jupiter 5.20 11.9
Saturn 9.58 29.4
-------------------------------------------------------------
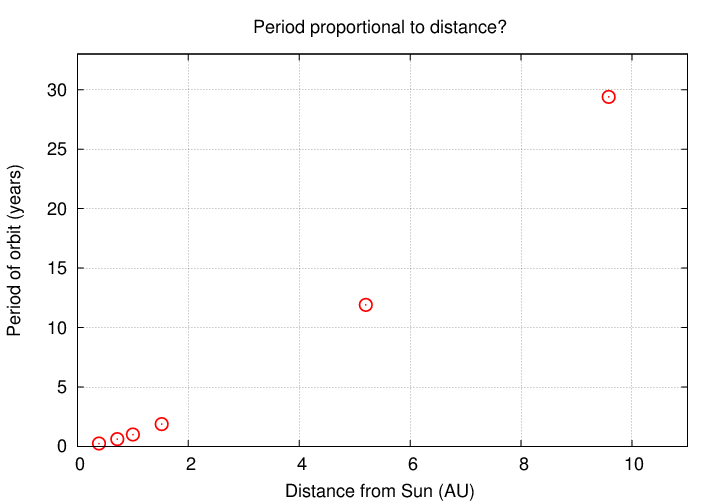
Q: Can you find a mathematical relationship between the
distance of a planet from the Sun, and its period?
It's pretty clear that a simple linear relationship won't work:
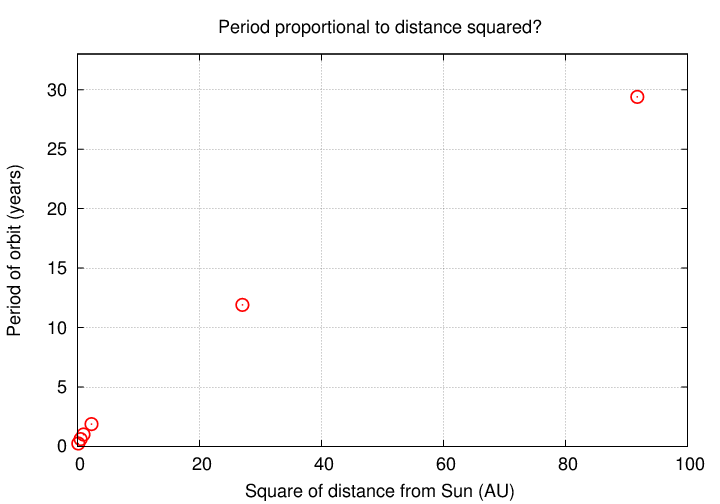
What about a quadratic relationship -- period increasing with the square of the distance?
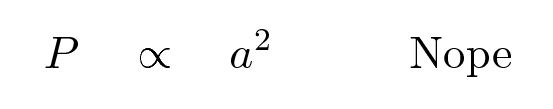
Is there ANY way to connect the period and distance mathematically? After years of searching, Kepler finally found it. He wrote in his magnum opus, Harmonia Mundi, or "The Harmony of the World",
" ...if you want the exact moment in time, it [the correct form of the law] was conceived mentally on 8th March in this year one thousand six hundred and eighteen, but submitted to calculation in an unlucky way, and therefore rejected as false, and finally returning on the 15th of May and adopting a new line of attack, stormed the darkness of my mind. So strong was the support from the combination of my labour of seventeen years on the observations of Brahe and the present study, which conspired together, that at first I believed I was dreaming, and assuming my conclusion among my basic premises. But it is absolutely certain and exact that the proportion between the periodic times of any two planets is precisely the sesquialterate proportion of their mean distances..."
The word "sesquialterate" means "raised to the three-halves power." Kepler's Third Law can be written in this form:
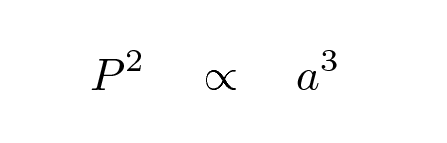
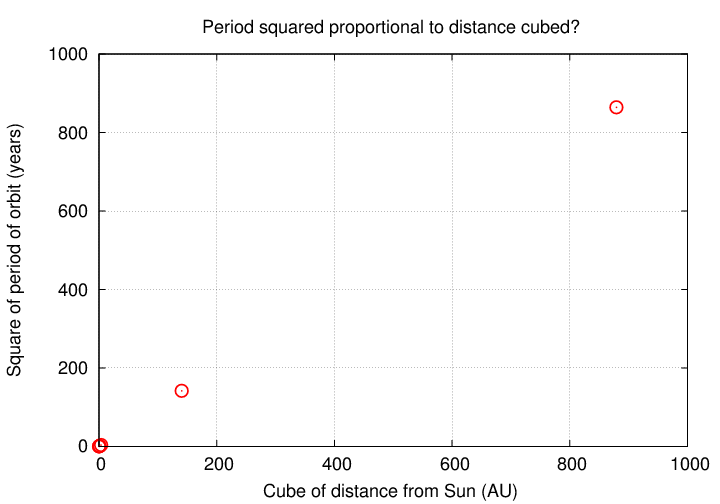
It's a bit hard to see that it works in practice, since the planets become separated by so much empty space on a graph ...
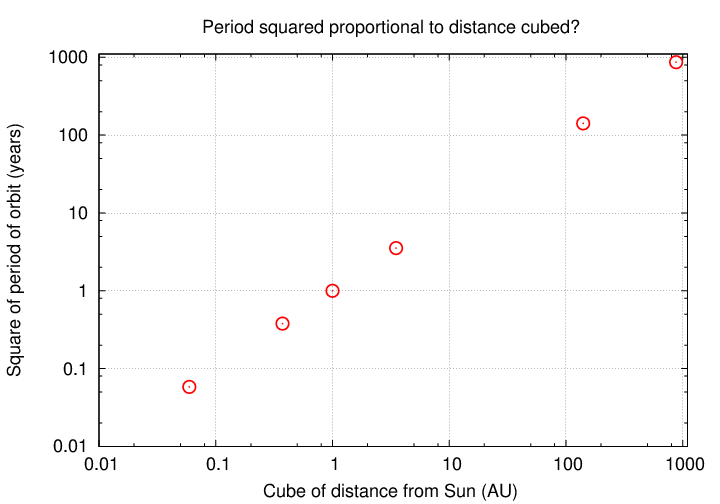
... but we can fix that by switching to logarithmic spacing on both axes:
You can check for yourself if you want -- just click the picture below to activate a little program.
Astronomy owes a great debt to Kepler. His hard work and imagination showed that IF scientists could break free from the assumptions they had made for centuries, they might find connections and relationships between the measured properties of planets. Some of his ideas weren't quite right -- he tried to explain the motion of the planets as due to a magnetic attraction from the Sun -- but that does not diminish his achievements.
About fifty years after Kepler's death, another scientist would show that all three of Kepler's Laws can be derived from even more fundamental rules governing the behavior of objects both in space and on the Earth.
Q: Who was this person who dug even deeper and
found the physical underpinnings of Kepler's Laws?
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.