Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Why do we call them "gas giants?" Because they are really big planets, much larger than the Earth. Look!
Source for the images can be found at
http://spiff.rit.edu/classes/resceu/ss_planets/earth_moon_lineup.html
Here's another comparison:
Image courtesy of
NASA/JPL-Caltech/SwRI/MSSS/Christopher Go
We can make the comparison quantitative, too. If we do, we can learn another difference between the terrestrial and gas giant planets.
Planet Radius Mass Density
(m) (kg) (kg/m^3)
-----------------------------------------------------------------------
Earth 6.37 x 106 5.97 x 1024
Jupiter 71.49 x 106 1898 x 1024
Saturn 60.27 x 106 568 x 1024
Uranus 25.56 x 106 86.8 x 1024
Neptune 24.76 x 106 102 x 1024
-----------------------------------------------------------------------
The densities of the giant planets are much lower than the densities of the terrestrial planets. Note that Saturn's density is less than that of water. It is often stated that
| Saturn would float in water! |
Image courtesy of NASA |
Rhett Allen provides some pretty good arguments against this scenario , but if it helps you to remember this feature of the giant planets, then, go right ahead and think it.
So, why are the densities of the gas giants so low? Well, you could just read the next section heading ...
Planets in the inner solar system are composed primarily of solid matter. The Earth, for example, has an iron core, a semi-solid mantle of dense minerals, with a solid crust floating on top. The atmosphere is just a tiny extra layer -- the skin of an apple has roughly the same relative thickness as the atmosphere of the Earth.
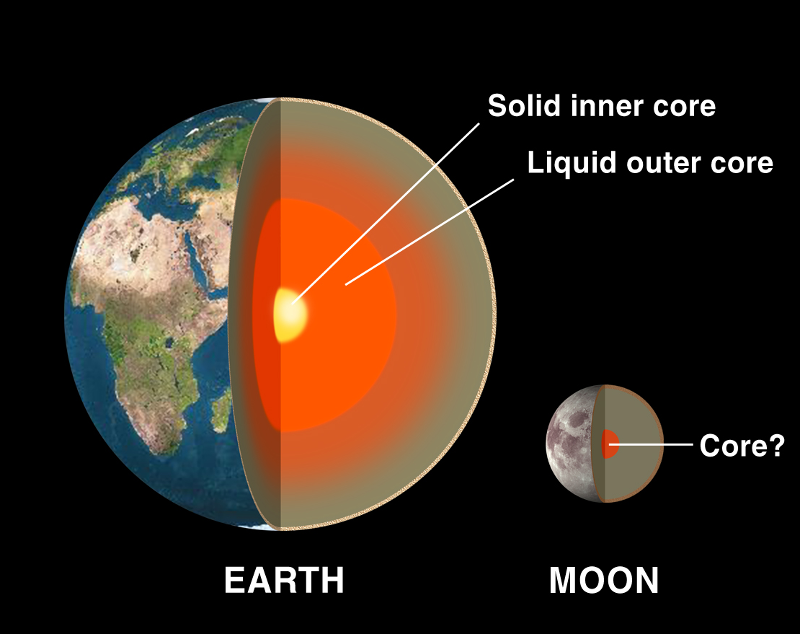
Image courtesy of
NASA (and Wikimedia)
But the atmospheres of the giant planets are more than a thin skin -- they occupy a large portion of the entire volume. In Jupiter and Saturn, the gaseous atmosphere accounts for roughly half the planet's radius; in Uranus and Neptune, perhaps a quarter.
Image courtesy of
NASA/Lunar and Planetary Institute
All four of the giant planets have moons -- and lots of them. Some of them are the largest moons in the Solar System, and quite a few are larger than our own Moon.
But there are also a plethora of much smaller objects in orbit around these giant planets. Since the smaller objects lack the gravitational force to overwhelm the structural forces within icy or rocky materials, they tend to be irregular in shape: potatoes, rather than spheres.
Here are the "big" Saturnian moons, from Titan at 5150 km (upper right) and Rhea at 1500 km (center) to little Hyperion, only about 250 km in diameter (lower right corner).
Image of some Saturnian moons courtesy of
NASA / JPL / SSI and Emily Lakdawalla
And these START with Hyperion at around 250 km, and go down to objects with diameters of just a few km. (Click on the image for a much larger and more detailed version).
Image courtesy of
NASA / JPL / SSI / Emily Lakdawalla. Satellite dimensions from Thomas et al (2013).
Some of these objects were formed together with their host planet, in the same swirling region of the proto-solar nebula, some 4.5 billion years ago. That's probably true for all the big satellites, with one exception which we'll discuss when we get to Neptune. But some of the smaller moons are very likely captured asteorids, objects that took a right turn at Albequerque, passed too close to a giant planet, and were unable to escape its gravitational attraction.
Compare the locations of the four big moons of Jupiter, with their nice, circular orbits ...
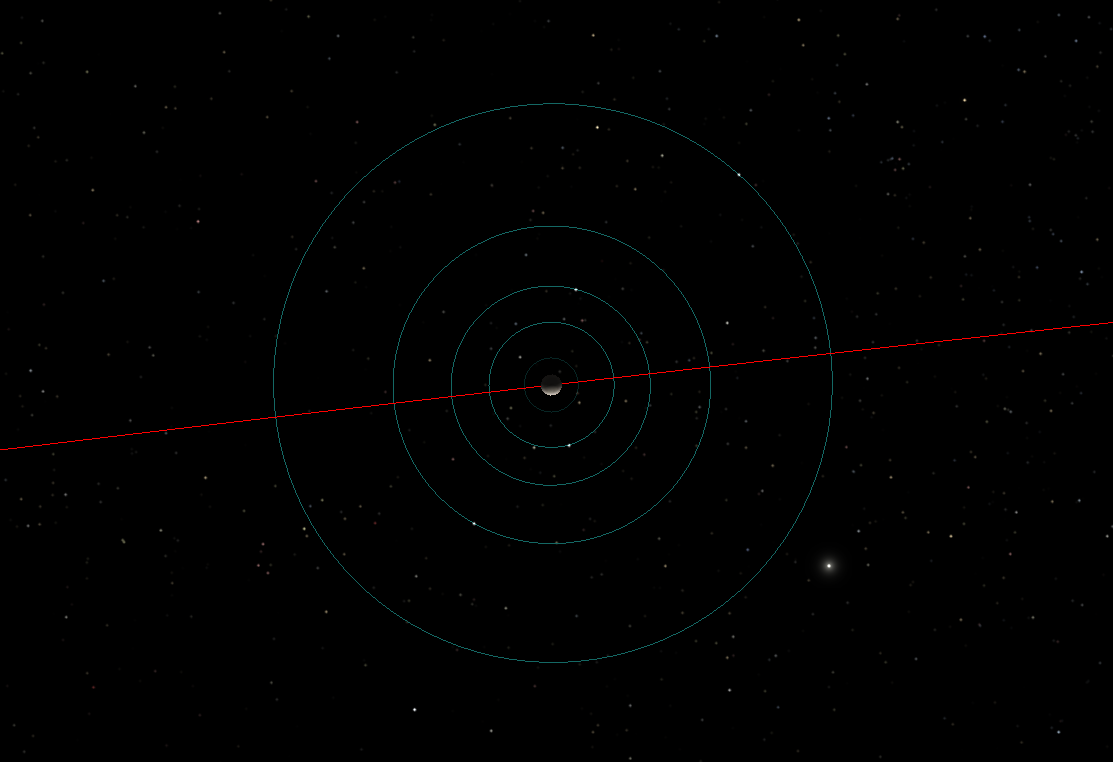
... to the locations of the smaller moons:
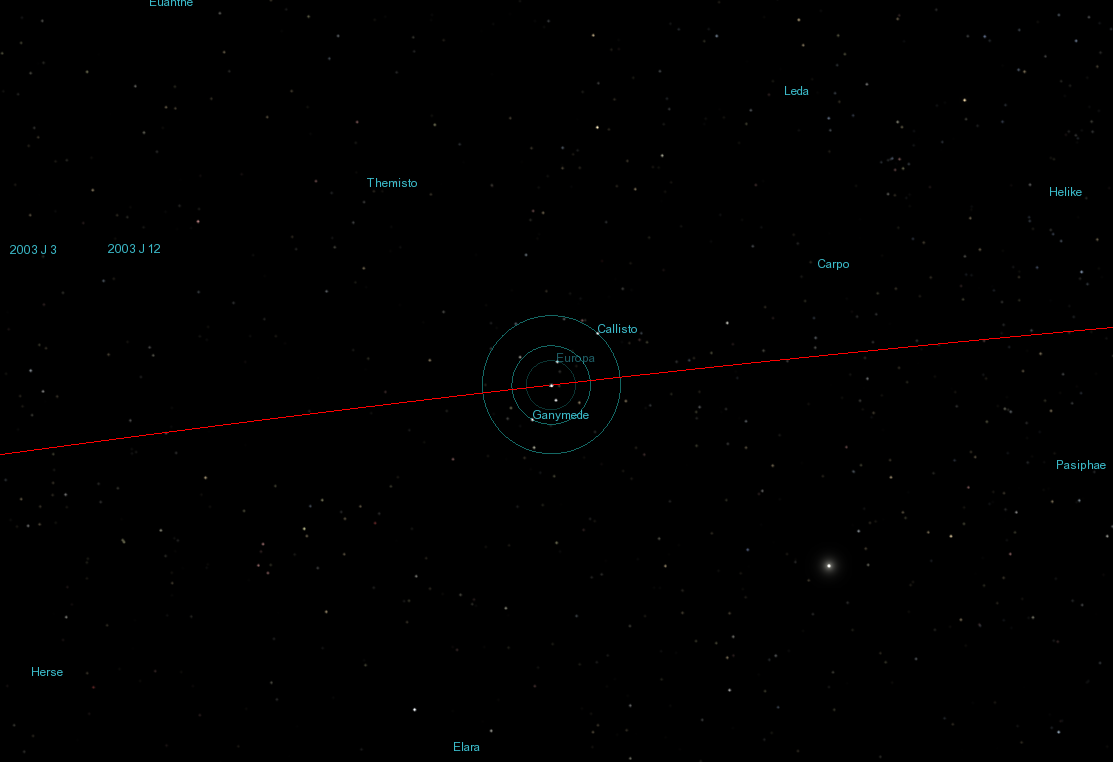
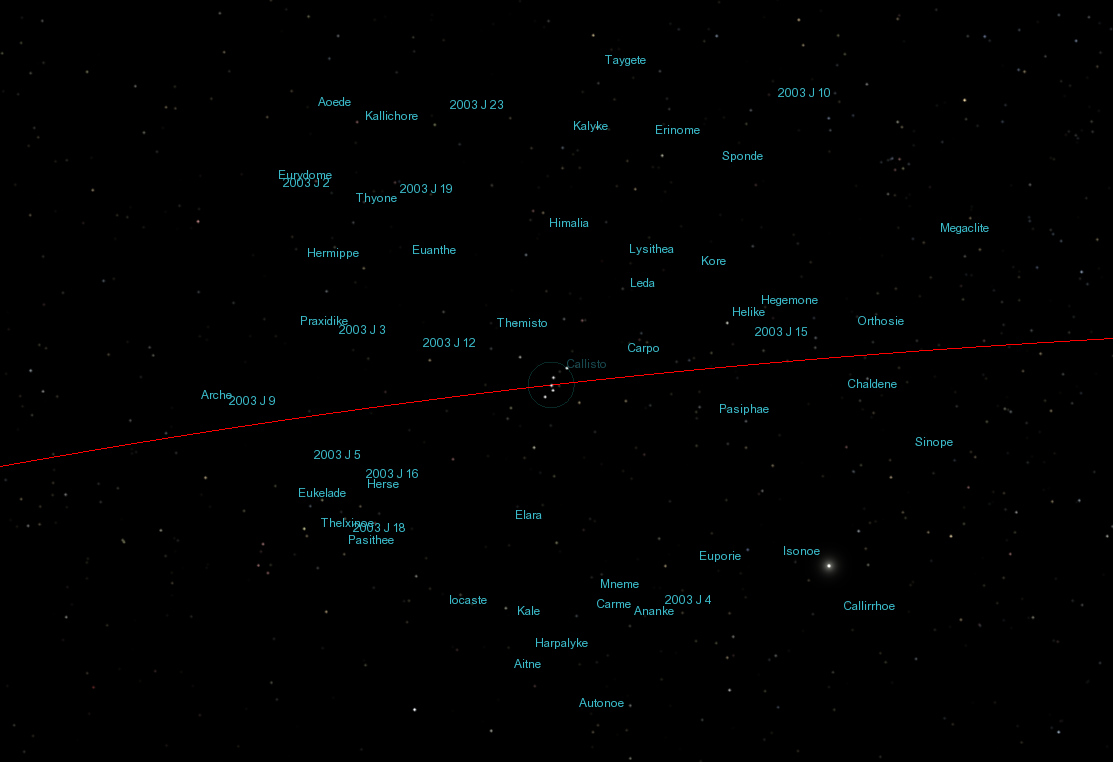
Most of the small, outermost moons have orbits that are retrograde -- in the direction opposite to Jupiter's own rotation, and the revolution of the inner moons. This is another clue that these objects didn't form together with Jupiter, but were captured long afterward. (Click on the image below to watch a short movie)
Video courtesy of
Carnegie Institution for Science
Astronomers are very glad that the gas giants have moons -- especially the big, bright ones -- because by measuring the orbital properties of these moons, we can deduce the mass of the planets. How? By a slight alteration of Kepler's Third Law. You remember it, right?
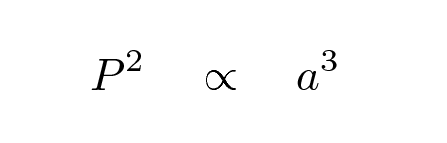
The equation works just fine, written as above, when we apply it to objects orbiting around the Sun, and use
But if we study objects orbiting around another body, like Jupiter, and continue to use the same units for period and semi-major axis, we need to make a small addition to the formula:
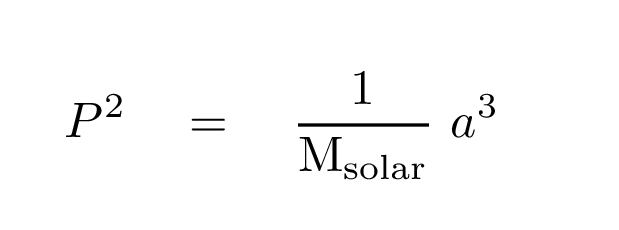
Give it a try!
Using the series of pictures showing the location of four
of Jupiter's moons below,
Then, convert your measurements to the proper units:
period in days
period P in years = --------------
365.25
semi-major axis a in AU = (distance in tick marks) * 3.17 x 10-3
Finally, you can use Kepler's Third Law to compute the mass of Jupiter. The result will be in solar units: the ratio of Jupiter's mass to the mass of the Sun.
Q: How large is the mass of Jupiter, compared to the mass of the Sun?
a) about 1/10 of the Sun's mass
b) about 1/100 of the Sun's mass
c) about 1/1000 of the Sun's mass
d) about 1/10,000 of the Sun's mass
Everyone knows that Saturn is surrounded by beautiful rings; even a small telescope in the backyard will show them clearly.
Image taken by Cassini, courtesy of
NASA/JPL-Caltech/Space Science Institute/G. Ugarkovic
But did you know that Jupiter has rings, too? They just aren't as big or as bright. The picture below, for example, was taken by the Galileo spacecraft as it flew through the shadow of Jupiter. A look back towards the Sun shows the faint, thin rings scattering light into the shadow.
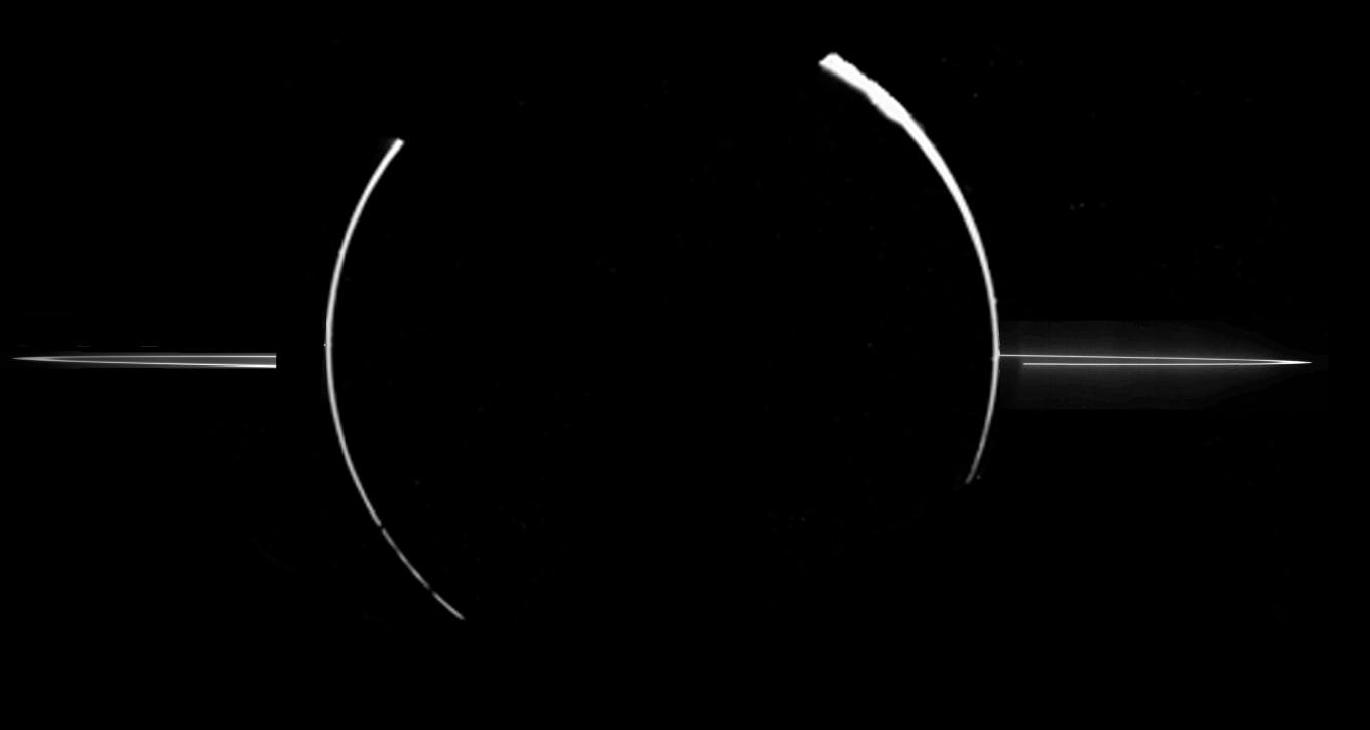
Image courtesy of
NASA, JPL, Galileo Project, (NOAO), J. Burns (Cornell) et al.
Jupiter's rings are due to tiny dust particles which are blasted off the surface of its inner moons by meteor impacts.
Uranus' rings were first noticed in 1977, when astronomers aboard NASA's Kuiper Airborn Observatory. The astronomers measured the brightness of a star as Uranus slowly moved past it. They noticed several short dips in brightness -- occultations -- before and then after the planet blocked the star.
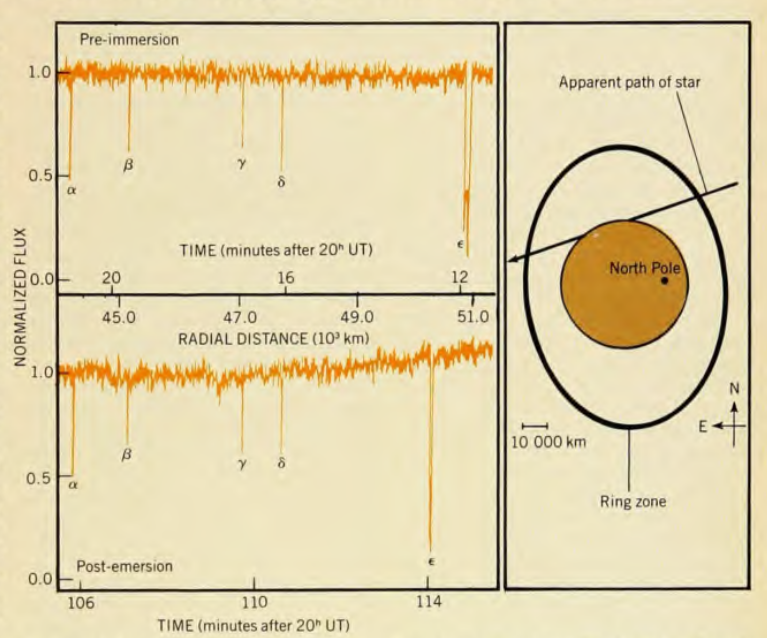
Image taken from
Physics Today, June 1977
based on data in
Millis, Wasserman and Birch, Nature 267, 330 (1977)
These rings are very faint and very thin, as a closeup taken by Voyager 2 in 1986 attests.
Image courtesy of
NASA/JPL
Neptune hid its rings very well. In the early 1980s, astronomers looked very hard for occultations which might reveal such rings, and found some evidence; but the definitive proof was not obtained until Voyager 2 swept past Neptune in 1989. These rings are also very thin, and very faint ...
Image courtesy of
NASA/JPL
... but they present a new twist: the particles in the rings aren't distributed uniformly, but in CLUMPS in some places.
Image courtesy of
NASA/JPL
Now, did you notice that word I used just a moment ago? I wrote the particles in the rings. How do we know that the rings are made of particles? Couldn't they be solid sheets of icy material?
Well, one way we know the answer is that, in the past few decades, we have spacecraft flying past the rings. Some of the pictures they have taken provide clear evidence that the rings are made of millions and billions of tiny little particles, not solid sheets.
Images of Saturn's F ring from
Voyager 1 (left) and Cassini (right) courtesy of
NASA/JPL
Image courtesy of
NASA/JPL/Space Science Institute
But a fellow named James Clerk Maxwell (does that name ring a bell?), way back in 1859, published a paper stating that the rings could NOT be solid sheets. He showed that only if the rings were made of tiny little particles, orbiting the planet individually, would the rings be stable over long periods.
Hooray, theory!
Long before any spacecraft visited Saturn, there was an observational confirmation of Maxwell's claim. Taking a spectrum of Saturn and its rings showed a pattern of features like this:
Spectrum of Saturn and rings taken from
Gingerich, Sky and Telescope, Nov 1964, p. 278
Notice how the lines are slanted in wavelength: each line is due to atoms which are absorbing light of one particular wavelength, but that wavelength can be modified by a Doppler shift if the atoms are moving.
Look at the lines in the upper half of the disk's spectrum: they shift to LONGER wavelengths as one moves from the center of the disk to the top edge, because that side of the disk is rotating AWAY from us. Now look at the absorption features of the rings on the same side of the planet.
If the rings are made of a solid sheet of material, the outer edges would be moving faster (away from us) than the inner edges, and so should be shifted to longer wavelengths.
Q: Do the features in the ring's spectrum above the planet
show the same slant toward longer wavelengths
at larger distance from the center of the planet?
No! They do not show fast motion away from us at larger radial distances. If anything, they show a slant the other way: towards slower motions at larger radial distances.
A solid sheet would rotate more quickly at the outer edges ... but tiny particles orbiting independently would move more slowly at the outer edges.
Q: Why would particles orbiting far from Saturn move more
slowly than particles orbiting close to Saturn?
Well, Mr. Kepler would explain it in terms of "sweeping out equal areas in equal times," and Mr. Newton would use terms like "gravitational force" and "inverse square law," but both would agree: objects orbiting Saturn will move more slowly if they are farther from the planet.
Hooray, measurements!
Remember what Zombie Feynman says:
The wonderful
XKCD comic is drawn by Randall Munroe
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.